3. Расчет подшипников

Радиальная нагрузка на опору A:

Радиальная нагрузка на опору B:

Опорой приводного вала на раму являются двухрядные сферические ролико‑подшипники. Расчет ведем по наиболее нагруженному подшипнику. На подшипник действуют только радиальные усилия, равные .

Назначаем типоразмер подшипника 2220 легкой широкой серии диаметров по ГОСТ 8328-75 с параметрами [3]: ;;; динамическая грузоподъемность; статическая грузоподъемность.

Определяем эквивалентную динамическую нагрузку

,

где – коэффициент долговечности.

Номинальная эквивалентная нагрузка определяется по зависимости

,

где – кинематический коэффициент, учитывающий снижение долговечности при неподвижном внутреннем кольце подшипника;– коэффициент безопасности при нагрузке с незначительными толчками;– температурный коэффициент при.

Тогда

и

Расчетная долговечность

,

где – коэффициент, учитывающий вероятность безотказной работы;– коэффициент, учитывающий совместное влияние качества металла и условий эксплуатации;– частота вращения приводного вала.

, что удовлетворяет требованиям.

Проверка подшипника по статической грузоподъемности

<С₀ = 276000Н

Подшипник А:

Среднее значение динамической грузоподъёмности для роликоподшипников:

.

Вычисляем заданный ресурс:

.

Коэффициент запаса по средним нагрузкам:

,

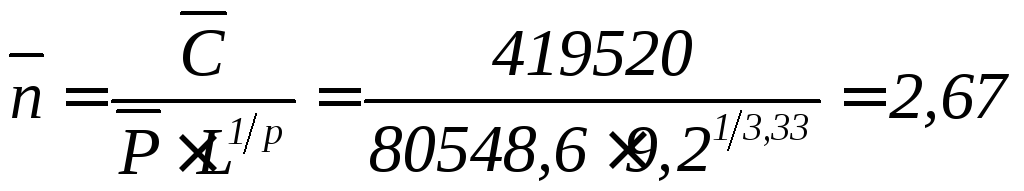где – среднее значение динамической эквивалентной нагрузки;– показатель степени для роликоподшипников.

Квантиль нормированного нормального распределения

,

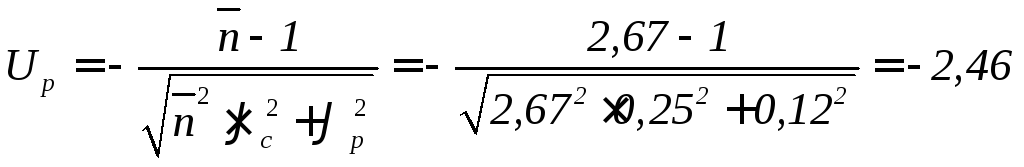По таблицам нормального распределения [2] в зависимости от полученного значения квантили находим, что вероятность безотказной работы рассчитываемого подшипника равна.

Исходя из экспоненциального закона распределения внезапных отказов, имеем:

,

где – для подшипников.

Подшипник B:

Среднее значение динамической грузоподъёмности для роликоподшипников

,

Коэффициент запаса по средним нагрузкам

,

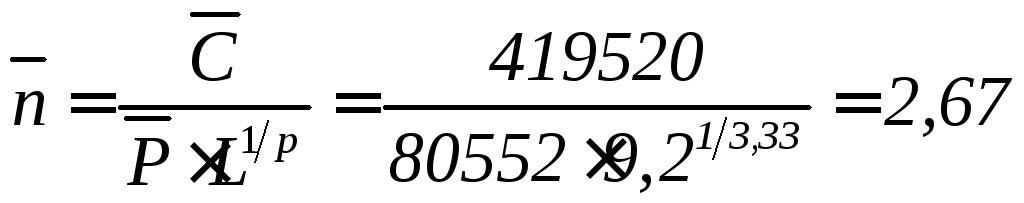где – среднее значение динамической эквивалентной нагрузки;– показатель степени для роликоподшипников.

Полагаем, что динамическая эквивалентная нагрузка и динамическая грузоподъемность распределены по нормальному или близкому к нормальному закону. Тогда вероятность безотказной работы определяем по квантили нормированного нормального распределения.

Квантиль нормированного нормального распределения

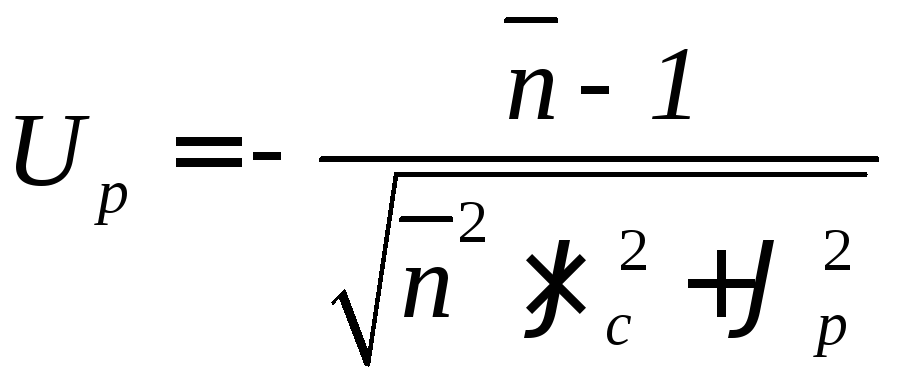
где и– коэффициенты вариации динамической грузоподъемности и динамической эквивалентной нагрузки.

Коэффициент вариации динамической грузоподъемности принимают равным для роликоподшипников.

Коэффициент вариации динамической эквивалентной нагрузки принимают равным коэффициенту вариации внешней нагрузки, действующей на подшипник, т.е. . Рекомендация основана на равенстве коэффициентов вариации случайных величин, связанных между собой линейной зависимостью.

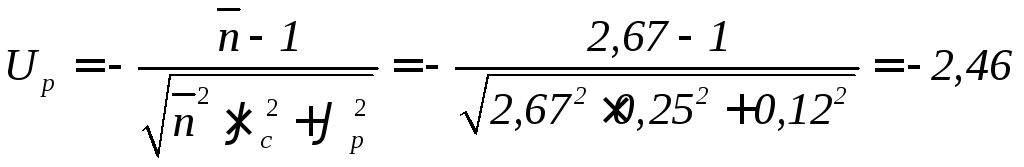
По таблицам нормального распределения в зависимости от полученного значения квантили находим, что вероятность безотказной работы рассчитываемого подшипника равна.

Исходя из экспоненциального закона распределения внезапных отказов, имеем:

,

где – для подшипников.

4. Расчет шпонок.

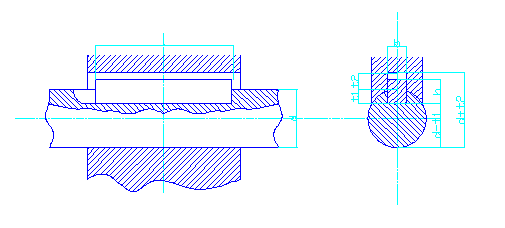
Основным для соединений с призматическими шпонками является условный расчет на смятие.

Шпонка 1,2:для вала диаметромпо ГОСТ 23360-78 предназначена шпонка со следующими размерами: ширина шпонки; высота шпонки; глубина паза на валу; длина шпонки.

Если принять для упрощения, что нормальные напряжения в зоне контакта распределены равномерно и плечо главного вектора давления равно , то

где – рабочая длина шпонки;– глубина врезания шпонки в ступицу колеса;– допускаемое напряжение смятия для шпонки, изготовленной из стали 45 [1, с. 89].

Принимаем длину шпонки равную в соответствии с длиной ступицы. Тогда. По формуле (2) проверяем напряжения в зоне контакта.

≤,

Проверку прочности шпонок на срез обычно не проводят, так как это условие соблюдается при использовании стандартных сечений шпонок.

Определим значение коэффициента запаса прочности

,

где – предел текучести наиболее слабого материала детали (вала, шпонки или ступицы),– коэффициент, учитывающий характер нагрузки и условия работы;– коэффициент, учитывающий погрешности монтажа и неравномерности распределения нагрузки по длине шпонки.

Квантиль нормированного нормального распределения

.

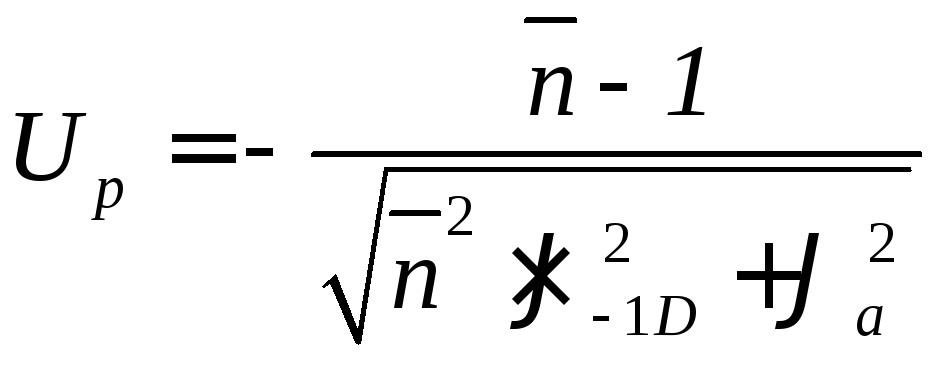Рассчитаем коэффициент вариации предела выносливости вала по нормальным напряжениям:

,

где – коэффициент вариации предела выносливости деталей из материала одной плавки при отсутствии рассеивания её размеров, обычно;– коэффициент вариации, характеризующий межплавочное рассеивание пределов выносливости образцов;– коэффициент вариации теоретического коэффициента концентрации напряжений.

Коэффициент вариации нагрузки равен .

По таблицам нормального распределения в зависимости от полученного значения квантили находим, что вероятность безотказной работы рассчитываемой шпонки равна.

Расчет шпонки под второй ступицей аналогичен, поэтому расчет не производим.