
Лекции по теории вероятностей
.PDFПусть = N0;1. Согласно ЦПТ, |
|
|
|
|
|
|
|
|
|
|
|
||||||||
P nn |
< E 1 = P pD |
|
|
nn |
E 1 |
< 0 ! P( < 0) = 0;1(0) = 2 |
6= P (E 1 < E 1) = 0: |
|
|||||||||||
1 |
|
||||||||||||||||||
S |
|
pn |
|
S |
|
|
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, кстати, ведет себя и вероятность P |
S |
. |
|
|
|
|
1 |
|
|||||||||||
n |
6 E 1 |
Она тоже стремится к |
|
, à |
|||||||||||||||
n |
2 |
||||||||||||||||||
íå ê P (E 1 6 E 1) = 1.
И изящное упражнение на ту же тему:
Упражнение 29. Доказать, что
0:999999n |
(n 1)! |
|
|
= 0; |
|||
n!1 |
Z0 |
|
|
||||
lim |
|
1 |
|
yn 1e y dy |
|
||
|
|
|
|
|
|||
n |
(n 1)! |
|
= 2; |
|
|||
n!1 Z0 |
|
|
|||||
lim |
1 |
|
yn 1e y dy |
1 |
|
||
|
|
|
|
||||
1:000001n |
(n 1)! |
|
|
= 1 |
|||
n!1 |
Z0 |
|
|
||||
lim |
|
1 |
|
yn 1e y dy |
: |
||
|
|
|
|
||||
У к а з а н и е. Каждый из интегралов равен функции распределения суммы независимых случайных величин с каким-то показательным распределением в некоторой точке. Вспомнить, что такое гамма-распределение и что такое «устойчивость относительно суммирования».
90

Раздел 15. Характеристические функции
p
Всюду в этой главе i = 1 — мнимая единица, t — вещественная переменная, eit = cos t + i sin t — формула Эйлера, E( + i ) = E + i E — способ вычисления математического ожидания комплекснозначной случайной величины + i , если математические ожидания ее действительной ( ) и мнимой ( ) частей существуют.
p
Как всегда, модулем комплексного числа z = x + iy называется jzj = x2 + y2, òàê ÷òî jeitj = 1.
Определение 53. Функция ' (t) = E eit называется характеристической функцией
случайной величины .
15.1Примеры вычисления
Пример 52. Пусть с. в. имеет распределение Бернулли с параметром p. Ее характеристическая функция (х. ф.) равна
' (t) = E eit = eit 0 P( = 0) + eit 1 P( = 1) = 1 p + peit:
Пример 53. Пусть с. в. имеет биномиальное распределение с параметрами n и p. Ее х. ф. равна
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
it |
X |
it k P |
X |
|
it k |
k |
k |
|
|
n k |
Xk |
k |
k |
|
|
n k |
n |
|
||||
' (t) = |
|
e |
|
= e |
|
( = k) = |
e |
|
Cn p |
|
(1 |
p) |
|
= |
Cn |
pe |
|
|
(1 |
p) |
|
= 1 p + pe |
|
|
: |
|
|
|
|
k=0 |
|
k=0 |
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
Последнее равенство суть бином Ньютона.
Пример 54. Пусть с. в. имеет распределение Пуассона с параметром . Ее х. ф. равна
|
|
|
E |
it |
|
|
1 |
it k P |
|
|
1 |
it k k |
|
|
|
1 |
( eit)k |
|
eit |
|
|
|
it |
|
|
|
|
||||||||
|
|
|
|
|
|
Xk |
|
|
|
|
X |
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
' (t) = |
|
e = |
|
e |
|
|
( = k) = |
e |
|
k! |
e |
|
= e |
k=0 |
|
|
k! |
|
= e e |
= expf |
|
e |
|
1 g: |
|
|
|||||||||
|
|
|
|
|
|
|
=0 |
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 55. |
Пусть с. в. имеет показательное распределение с параметром . Ее |
||||||||||||||||||||||||||||||||||
х. ф. функция равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
' (t) = E eit = Z |
eit x f (x) dx = Z |
eitx e x dx = Z |
e x( it) dx = |
|
e x( it) 0 |
|
= |
|
; |
||||||||||||||||||||||||||
it |
|
it |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поскольку при x |
! 1 |
модуль величины e x( it) |
= e x |
|
eitx |
|
|
|
|
|
|
e x( it) |
= |
||||||||||||||||||||||
e x |
! |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стремится к нулю: |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 56. Пусть с. в. имеет гамма-распределение с параметрами , . Ее х. ф. равна
11
' (t) = E eit = Z0 |
eit x f (x) dx = Z0 |
eitx |
|
|
x 1 e x dx = |
|
|
|
|
|
|
|
|
|
|
|
||
( ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
= 1 |
it |
|
|
|
|
|
|
|
= |
|
Z0 |
x 1 e x( it) dx = |
|
: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
( ) |
it |
|
|
|
|||||||||||
91

Интеграл мы вычислили с помощью гамма-функции Эйлера:
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
) |
|
|
|||
|
Z x 1 e x( it) dx = |
|
1 |
Z (x( it)) 1 e x( it) dx( it) = |
( |
: |
|
||||||||||||||||
( |
it) |
( it) |
|
||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
Пример 57. |
Пусть с. в. |
|
имеет стандартное нормальное распределение. Ее х. ф. |
||||||||||||||||||||
равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Z |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
' (t) = |
p |
|
eitx e x |
=2 dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
Z |
2 |
2 |
2 |
1 |
Z |
2 |
|
|
2 |
|
|||||
|
|
|
|
|
= |
p |
|
|
e t |
=2 e (x it) |
=2 dx = e t |
=2 |
p |
|
e (x it) |
=2 d(x it) = e t |
=2: |
||||||
|
|
|
|
|
2 |
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Как всегда, при интегрировании мы выделили полный квадрат в показателе экспоненты и
вспомнили, чему равен интеграл по всей прямой от функции p1 e u2=2. А чему он равен?
2
Самое время остановиться и спросить: "Ну и что? Зачем нам эти функции и какой от них прок?" Приглашаю читателя познакомиться с замечательными свойствами х. ф.
15.2Свойства характеристических функций
Ô1. Характеристическая функция всегда существует:
j' (t)j = jE eit j 6 E jeit j = E 1 = 1
Полезно вспомнить, что обычные математические ожидания существуют не у всех распределений.
Ô2. По характеристической функции однозначно восстанавливается распределение (функция распределения, а также плотность или таблица распределения). То есть если две с. в. имеют одинаковые х. ф., то и распределения этих с. в. совпадают.
Формулы, с помощью которых это делается, в анализе называют формулами «обратного преобразования Фурье». Например, если модуль х. ф. интегрируем на всей прямой, то у с. в. есть плотность распределения, и она находится по формуле (проверьте на примере примера 57)
1 |
e itx ' (t) dt: |
||
f (x) = 2 Z |
|||
1 |
|
|
|
|
|
1 |
|
Ни одна из формул обратного преобразования Фурье нам не понадобится.
Ô3. Характеристическая функция с. в. a + b связана с х. ф. случайной величины равенством
'a+b (t) = E eit(a+b ) = eita ' (tb):
92

Пример 58. Вычислим х. ф. случайной величины , имеющей нормальное распре-
деление с параметрами a и 2. Мы знаем, что у стандартизованной с. в. = |
a |
харак- |
|
|
|||
|
|
теристическая функция равна ' (t) = e t2=2. Тогда х. ф. случайной величины = a + равна
' (t) = 'a+ (t) = eita ' (t ) == eita e (t )2=2 = exp ita t2 2 :
2
Ô4. Характеристическая функция суммы независимых с. в. равна произведению характеристических функций слагаемых: если с. в. и независимы, то, по свойству E6 математических ожиданий
' + (t) = E eit( + ) = E eit E eit = ' (t) ' (t):
Этим замечательным свойством мы сразу же воспользуемся, как обещали, для доказательства леммы 6, утверждающей устойчивость нормального распределения относительно суммирования.
Пример 59. Доказательство леммы 6.
Пусть случайные величины = Na1; 12 è = Na2; 22 независимы. Характеристическая функция суммы + равна
' + (t) = ' (t) ' (t) = exp ita1 |
t2 2 |
exp |
ita2 |
t |
2 2 |
= exp |
it(a1 + a2) |
t2 |
( |
2 |
+ |
2 |
: |
1 |
2 |
|
1 |
2) |
|||||||||
2 |
|
2 |
|
|
|
2 |
|
То есть х. ф. суммы есть характеристическая функция нормального распределения с параметрами a1 + a2, 12 + 22. Тогда + = Na1+a2; 12+ 22 по свойству 2.
Пример 60. Докажем свойства устойчивости по суммированию биномиального распределения, распределения Пуассона и гамма-распределения (леммы 4, 5, 7), используя вычисленные в примерах 52–56 характеристические функции.
Для независимых с. в. с распределениями Пуассона и х. ф. суммы
' + (t) = ' (t) ' (t) = exp eit 1 exp eit 1 = exp ( + ) eit 1
равна характеристической функции распределения Пуассона с параметром + .
Для независимых с. в. с биномиальными распределениями Bn;p è Bm;p х. ф. суммы
' + (t) = ' (t) ' (t) = 1 p + peit n 1 p + peit m = 1 p + peit n+m:
равна характеристической функции биномиального распределения с параметрами n+m, p.
Для n независимых с. в. с показательным распределением E х. ф. суммы
' 1+ + n (t) = (' 1 (t))n |
= |
|
|
n |
= 1 |
it |
|
n |
|
|
|
|
|
|
|||||
it |
|
|
|
||||||
равна характеристической функции гамма-распределения с параметрами , n.
93
Ô5. Пусть существует момент порядка k = 1; 2; : : : случайной величины , то есть Ej jk < 1. Тогда ее характеристическая функция ' (t) непрерывно дифференцируема k раз, и ее k-я производная в нуле связана с моментом порядка k равенством:
(k) |
(0) = |
|
dk |
|
t=0= |
E ik k eit |
|
t=0= ik E k: |
|
' |
d tk E eit |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Существование и непрерывность k-й производной, равно как и законность переноса производной под знак математического ожидания мы доказывать не будем.
Упражнение 30. Доказать, что для с. в. со стандартным нормальным распределе-
2k def
нием момент четного порядка 2k равен = (2k 1)!! = (2k 1) (2k 3) : : : 3 1.
E
Доказать по определению, что все моменты нечетных порядков стандартного нормального распределения существуют и равны нулю.
Как только появились производные высших порядков, самое время разложить функцию в ряд Тейлора.
Ô6. Пусть существует момент порядка k = 1; 2; : : : случайной величины , то есть Ej jk < 1. Тогда ее характеристическая функция ' (t) в окрестности точки t = 0 разлагается в ряд Тейлора
k |
tj |
(j) |
k |
ijtj |
|
|
|
|
|
Xj |
|
|
X |
|
|
|
|
|
|
|
' (0) + o(jtkj) = 1 + |
j! E j + o(jtkj) = |
|
|
|||||
' (t) = ' (0) + |
j! |
j=1 |
|
|
|||||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
iktk |
||
|
|
|
= 1 + it E |
|
E 2 + : : : + |
|
E k + o(jtkj): |
||
|
|
|
2 |
k! |
|||||
Ряды Тейлора, как правило, возникают при предельном переходе. Следующее основное свойство характеристических функций потребуется нам для доказательства предельных теорем, и это свойство — последняя теорема, оставленная нами без доказательства.
Теорема 35 (Теорема о непрерывном соответствии). Случайные величины
n слабо сходятся к с. в. тогда и только тогда, когда для любого t характеристические функции ' n (t) сходятся к характеристической функции ' (t).
Сформулированная теорема устанавливает непрерывное соответствие между классами hF ; ) i функций распределения со слабой сходимостью и h' ; !i характеристических функций со сходимостью в каждой точке. «Непрерывность» этого соответствия — в том, что пределу в одном классе относительно заданной в этом классе сходимости соответствует предел в другом классе относительно сходимости, заданной в этом классе.
Осталось воспользоваться теоремой о непрерывном соответствии и доказать
ЗБЧ в форме Хинчина и ЦПТ.
94

15.3Доказательство ЗБЧ Хинчина
Пусть 1; 2; : : : — последовательность независимых и одинаково распределенных слу- чайных величин с конечным первым моментом Ej 1j < 1. Обозначим через a математиче-
ское ожидание E 1. Требуется доказать, что |
|
|
|||
|
Sn |
= |
1 + + n |
p |
a: |
|
n |
n |
! |
||
|
|
|
|||
По свойству 19 сходимость по вероятности к постоянной эквивалентна слабой сходимости.
|
n |
|
n |
) |
|
Так как a — постоянная, достаточно доказать слабую сходимость |
Sn |
= |
1 + + n |
|
a. |
|
|
|
По теореме о непрерывном соответствии, эта сходимость имеет место, если и только если для любого t 2 R сходятся характеристические функции
'Sn=n(t) ! 'a(t) = E eita = eita: |
|
|||||||
Найдем характеристическую функцию с. в. |
Sn |
. Пользуясь свойствами Ô3 è Ô4, получим |
||||||
|
|
n |
||||||
|
|
|
|
|
|
|
|
|
3 |
t |
4 |
|
t |
|
n |
||
|
|
|
||||||
'Sn=n(t) = 'Sn |
|
|
= ' 1 |
|
|
: |
||
n |
n |
|||||||
Вспомним, что первый момент 1 существует, поэтому свойство Ô6 позволяет разложить
' 1 (t) в ряд Тейлора в окрестности нуля ' 1 (t) = 1 + it E 1 + o(jtj) = 1 + ita + o(jtj). В точке t=n, соответственно,
' 1 n |
= 1 + n |
+ o n ; |
'Sn=n(t) = |
' 1 |
n |
n |
|
|
n |
n |
||||||||||||
= 1 + n + o |
: |
|||||||||||||||||||||
|
t |
ita |
|
t |
|
|
|
|
|
|
|
|
t |
|
|
|
|
ita |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
n |
x |
|
|
|
|
|
|
При n ! 1, пользуясь «замечательным |
пределом» 1 + nn |
|
|
! e |
, получим |
|
|
|
|
|||||||||||||
|
|
|
'Sn=n |
(t) = |
1 + n + o |
n |
! eita; |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
ita |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
15.4Доказательство центральной предельной теоремы
Пусть 1; 2; : : : — последовательность независимых и одинаково распределенных слу- чайных величин с конечной и ненулевой дисперсией. Обозначим через a математическое ожидание E 1 и через 2 — дисперсию D 1. Требуется доказать, что
Sn na |
= |
1 + + n na |
|
N |
: |
||||
|
|
|
|
|
|
|
|||
pn |
|
pn |
) |
0;1 |
|
||||
Введем стандартизованные случайные величины i = i a — независимые с. в. с нулевы-
ми математическими ожиданиями и единичными дисперсиями. Пусть Zn есть их сумма Zn = 1 + + n = (Sn na)= . Требуется доказать, что
pZnn ) N0;1:
95

p
Характеристическая функция величины Zn= n равна
'Zn=pn(t) = 'Zn |
pn |
= ' 1 |
pn |
n |
(25) |
||||||||
: |
|||||||||||||
|
|
3 |
|
t |
4 |
|
t |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Характеристическую функцию с. в. 1 можно разложить в ряд Тейлора, в коэффициентах которого использовать известные моменты E 1 = 0, E 12 = D 1 = 1. Получим
6 |
|
t2 |
t2 |
||
' 1 (t) = 1 + it E 1 |
|
|
E 12 + o(t2) = 1 |
|
+ o(t2): |
2 |
2 |
||||
p
Подставим это разложение, взятое в точке t= n, в равенство (25) и устремим n к бесконечности. Еще раз воспользуемся замечательным пределом.
|
|
|
|
t |
|
n |
t2 |
2 |
|
n |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
'Zn=p |
|
(t) = ' 1 |
|
p |
|
|
= 1 |
|
+ o |
|
t |
|
|
! exp |
t |
|
ïðè n ! 1: |
n |
|
||||||||||||||||
2n |
n |
|
2 |
||||||||||||||
n |
|
||||||||||||||||
В пределе получили характеристическую функцию стандартного нормального закона. По теореме о непрерывном соответствии можно сделать вывод о слабой сходимости
pZnn = Sn pnna ) N0;1
распределений стандартизованных сумм к стандартному нормальному распределению, что и утверждается в ЦПТ.
Попробуйте теперь сами:
Упражнение 31. Пусть при любом > 0 случайная величина имеет распределение Пуассона с параметром . Используя теорему о непрерывном соответствии, доказать, что случайные величины
p
слабо сходятся к стандартному нормальному распределению при ! 1. Характеристическая функция с. в. вычислена в примере 54.
96

Раздел 16. Доказательство теоремы Пуассона
Нам осталось доказать теорему Пуассона. В доказательство будут использоваться только свойства устойчивости биномиального и пуассоновского распределений относительно операции суммирования. Никакие разделы, связанные с числовыми характеристиками с. в., сходимостями или характеристическими функциями, нам в доказательстве не понадобятся.
Вспомним утверждение, которое мы собрались доказывать. Теперь, когда мы знакомы с термином «распределение», можно сформулировать теорему Пуассона так:
Теорема Пуассона с оценкой погрешности
Пусть A f0; 1; 2; : : : ; ng — произвольное множество целых неотрицательных чисел, случайная величина n имеет биномиальное распределение Bn;p с параметрами n и p, случайная величина n имеет распределение Пуассона с параметром = np. Тогда
j P( n 2 A) P( n 2 A) j = |
Cnk pk (1 p)n k |
|
k! |
e |
6 np2 = n |
: |
|
|
k2A |
k2A |
k |
|
|
2 |
|
|
X |
X |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Иначе говоря, требуется доказать, что
sup j P( n 2 A) P( n 2 A) j 6 np2:
A
Доказательство проведем, используя так называемый «метод одного вероятностного пространства». Нам нужно оценить сверху разницу между двумя распределениями, а именно: доказать, что для любых множеств A f0; 1; 2; : : : ; ng разницу между вероятностями попадания в множество A биномиальной (с параметрами n и p) и пуассоновской (с параметром np) случайных величин можно оценить величиной np2.
Заметим, прежде всего, что разность
X
j P( n 2 A) P( n 2 A) j =
k2A
Cnk pk (1 p)n k |
X |
k |
|
||
k2A |
k! |
|
|
|
e
никак не зависит от того, каким образом величины n è n взаимосвязаны и на каком вероятностном пространстве заданы, если только одна из этих величин имеет биномиальное, а вторая — пуассоновское распределение с нужными параметрами. Совместное распределение этих величин тут никак не участвует, поэтому данная разность не изменится, если заменить n è n íà другие случайные величины с теми же распределениями.
Первое, что мы сделаем — докажем, что для двух случайных величин и (где угодно заданных) «расстояние между распределениями», то есть supA j P( 2 A) P( 2 A) j, íå
больше, чем вероятность P |
~ |
|
~ |
|
6= ~ äâóì произвольным случайным величинам ; ~ с данны- |
||
ми распределениями не совпадать. |
Понятно, что эти новые с. в. должны быть заданы |
||
на одном вероятностном пространстве, и наилучшая оценка сверху получится, если нам
удастся так задать на одном вероятностном пространстве с. в. ~, распределенную как ,
и , распределенную как , чтобы вероятность ~ 6 была наименьшей
~ P = ~ .
97

Лемма 9 (Неравенство каплинга). Пусть и — произвольные с. в. Пусть слу-
чайная величина ~ одинаково распределена с , случайная величина одинаково распреде-
~
~ |
|
|
|
|
|
лена с , и величины ; ~ заданы на одном вероятностном пространстве. Тогда |
|||||
A R j |
2 |
( 2 ) j 6 |
|
|
6= ~ |
sup P( |
A) |
P A |
P |
~ |
: |
|
|||||
Замечание 28. Каплингом (coupling) двух с. в. и называют задание на одном веро-
~ |
|
ятностном пространстве случайных величин , распределенной как , и ~, распределенной |
|
êàê . |
|
Доказательство неравенства каплинга. Воспользуемся |
равенством |
P(C) = P(C \ B) + P(C \ B), а также тем, что вероятность пересечения двух событий не превосходит вероятности любого из них. Для любого множества A R
2 ~ 2 ~ 2 ~ ~ 2 ~ 6 2 ~ ~ 2 ~ 6
P( A) = P A = P A; = ~ + P A; = ~ = P ~ A; = ~ + P A; = ~ 6
2 ~ 6 2 ~ 6
6 (~ A) + = ~ = ( A) + = ~ ;
P
P
P
P
òî åñòü
2 2 ~ 6
( A) ( A) 6 = ~ :
P
P
P
Поменяем местами и и получим, что для любого множества A R
j 2 2 j ~ 6
P( A) P( A) 6 P = ~ :
Займемся заданием на одном вероятностном пространстве величин ~n è ~n, распределенных как n è n, соответственно.
Пусть 1; : : : ; n — независимые случайные величины, имеющие распределение Бернулли с параметром p. Тогда их сумма ~n = 1 + : : : + n имеет биномиальное распределение с параметрами n и p, то есть одинаково распределена с n.
Пусть 1; : : : ; n — независимые случайные величины, имеющие распределение Пуассона с параметром p. Тогда их сумма ~n = 1 + : : : + n также имеет распределение Пуассона с параметром, равным сумме параметров слагаемых, то есть np, и одинаково распределена с n. Мы будем считать, что эти наборы с. в. сразу заданы на одном вероятностном пространстве, и позже построим их.
Тогда, в силу неравенства каплинга,
j P( n 2 A) P( n 2 A) j 6 P (~n 6= ~n) = P |
=1 i 6= |
i=1 i! |
: |
|
n |
n |
|
|
Xi |
X |
|
Заметим теперь, что если две суммы с неотрицательными слагаемыми не равны друг другу, то хотя бы одно слагаемое в первой сумме отличается от соответствующего слагаемого в другой сумме (иначе...). Поэтому
j P( n 2 A) P( n 2 A) j 6 P |
i=1 i 6= |
i=1 i! |
6 P |
i=1 f i 6= ig! |
6 |
=1 P ( i 6= i) : (26) |
|
n |
n |
|
n |
|
n |
|
X |
X |
|
[ |
|
Xi |
В последнем неравенстве использовано, что вероятность объединения не превосходит суммы вероятностей.
98
Осталось теперь так задать на одном вероятностном пространстве i è i, чтобы минимизировать P ( i 6= i).
Пусть множество элементарных исходов есть n-мерный куб, стороны которого — отрезки [0; 1] на осях координат, вероятность есть просто мера Лебега, заданная на - алгебре борелевских множеств.
Вот ровно сейчас тот, кто поленился о них прочитать, должен об этом пожалеть!
То есть мы наудачу выбираем точку ! = (!1; : : : ; !n) в кубе, или, что то же самое, каждую из координат !i выбираем наудачу и независимо от других на [0; 1].
Построим для каждого i = 1; : : : ; n по !i случайные величины i = i(!i) è i = i(!i) с нужными распределениями, чтобы они, к тому же, совпадали с большой вероятностью. Положим
i |
i |
|
(1; |
åñëè 1 |
p 6 !i |
6 1: |
|
(! |
) = |
0; |
åñëè 0 |
6 !i < 1 |
p; |
Эта с. в. имеет распределение Бернулли: P( i = 0) = P(0 6 !i < 1 p) = 1 p, P( i = 1) =
P(1 p 6 !i 6 1) = p.
|
Случайная величина i должна иметь распределение Пуассона с параметром p, то есть |
|||
|
|
pk |
|
|
pk |
= P( i = k) = |
|
e p |
при k = 0; 1; 2; : : : . Сумма этих вероятностей равна 1, поэтому |
|
||||
|
|
k! |
|
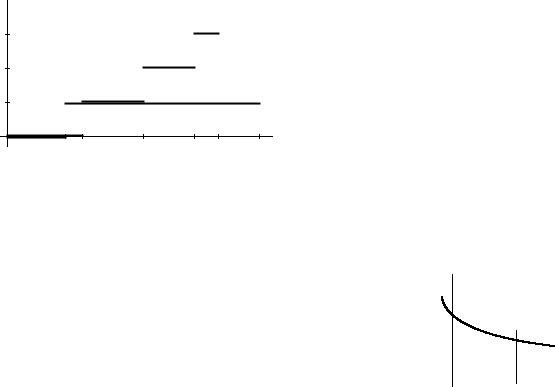
|
можно разбить тот же самый отрезок [0; 1] на отрезки, длина k-го из которых равна pk при k = 0; 1; 2; : : : , и положить i = k, åñëè !i принадлежит отрезку с номером k:
6
3
2
1
1 p |
|
p |
|
0 |
|
0 |
|
p |
= |
+ |
|
|
e |
p |
|
|
|
|
|
|
|
p |
1 |
: : :
i
i
p |
: : : |
0 |
|
+ |
|
|
p |
|
1 |
|
+ |
|
p |
|
2 |
|
|
|
81; |
åñëè p066 !i i < p0 + p1; |
||||
|
|
|
> |
0; |
åñëè 0 |
! |
< p0; |
|
|
|
|
>2; |
åñëè p0 |
+ p1 |
|
!i < p0 + p1 + p2; |
|
|
(! |
) = |
> |
|
|
|
6 |
|
> |
|
|
|
|
|
|||
i |
i |
|
> |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
>: : : |
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
1-!i |
|
|
>k; |
åñëè p0 + : : : + pk 1 6 !i < p0 + : : : + pk; |
||||
|
|
|
> |
|
|
|
|
|
>
>
>
>
>
>
:: : :
С очевидностью, получим с. в. с распределением Пуассона:
P( i = k) = P(p0 + : : : + pk 1 6 !i < p0 + : : : + pk 1 + pk) = pk; k = 0; 1; 2; : : : :
|
|
p0 |
|
|
Отметим, что p0 |
= |
|
e p |
= e p. Докажем, что |
|
||||
|
0! |
|
|
|
e p > 1 p ïðè p > 0. |
|
|||
Действительно,
а) при p = 0 значения функций совпадают: e 0 = 1
6
1 @ |
e p |
@ |
|
|
1 |
@ |
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
@ |
- |
|
|
|
@ |
|
0 |
|
1 @ |
p |
|
0 = 1;
99
