
§7.5. Экстремум в системах функций
Изучение экстремумов математических объектов, задаваемых несколькими функциями, является более сложной задачей. В общем случае задачу можно сформулировать так: найти экстремум функции , заданной системой функций
![]() (13)
(13)
К такой системе сводится задача на условный
максимум производственной функции
такой системе сводится задача на условный
максимум производственной функции ![]() при бюджетном ограничении
при бюджетном ограничении ![]() ,
в котором денежные средства
,
в котором денежные средства ![]() ,
отпущенные на закупку ресурсов, уже не
являются постоянной величиной
,
отпущенные на закупку ресурсов, уже не
являются постоянной величиной ![]() ,
а зависят от величины выпуска
,
а зависят от величины выпуска ![]() и «подпитываются» долей дохода:
и «подпитываются» долей дохода: ![]() .
Чем лучше работает предприятие, тем
большие средства оно может отпустить
на закупку сырья, энергообеспечение,
аренду и т.д. Задача на условный экстремум
с переменным бюджетным ограничением
формулируется так
.
Чем лучше работает предприятие, тем
большие средства оно может отпустить
на закупку сырья, энергообеспечение,
аренду и т.д. Задача на условный экстремум
с переменным бюджетным ограничением
формулируется так
![]()
Н а
рис.7.18 изображен график функции
Кобба-Дугласа. Рассмотрены три варианта
уравнения связи. При
а
рис.7.18 изображен график функции
Кобба-Дугласа. Рассмотрены три варианта
уравнения связи. При ![]() условный экстремум находится в точке
условный экстремум находится в точке
![]() .
Если
.
Если ![]() ,
условный максимум перемещается в точку
,
условный максимум перемещается в точку
![]() .
Наконец, при
.
Наконец, при ![]() условный максимум оказывается в точке
условный максимум оказывается в точке
![]() .
.
Если величина ![]() возникает положительная обратная
связь, если
возникает положительная обратная
связь, если ![]() -
отрицательная. Простым преобразованием
второго уравнения задача с обратной
связью сводится к исследованию на
экстремум в системе функций
-
отрицательная. Простым преобразованием
второго уравнения задача с обратной
связью сводится к исследованию на
экстремум в системе функций

Поиск решения начнем с нахождения множества таких точек на координатной плоскости Oxy, в которых значения функций системы равны
![]() .
.
Решение этого уравнения
подставим в одну из функций
![]() и исследуем на экстремум функцию
и исследуем на экстремум функцию
![]() .
Критическая точка
для функции
задает стационарную точку
на плоскости Oxy, в
которой возможен экстремум
.
Критическая точка
для функции
задает стационарную точку
на плоскости Oxy, в
которой возможен экстремум
![]() .
.
Поскольку
![]() и
и
![]() ,
найдем производную по
,
которая в критической точке
будет равна нулю:
,
найдем производную по
,
которая в критической точке
будет равна нулю:
![]() и
и
![]()
Отсюда при условии
![]() и
и
![]() получим
получим
![]()
![]() (14)
(14)
Найденное выражение представляет необходимые условия в задаче на условный экстремум с обратной связью.
Метод Лагранжа при исследовании на условный экстремум в системах функций
Поскольку каждое уравнение системы при
исследовании на экстремум можно привести
к виду ![]() и
и ![]() ,
то в критической точке должен быть
равен нулю дифференциал каждой функции
,
то в критической точке должен быть
равен нулю дифференциал каждой функции
![]()
![]()
Умножим первое и второе равенства на
![]() и
и ![]() соответственно, причем
,
не равны нулю одновременно
соответственно, причем
,
не равны нулю одновременно
![]()
Слева в равенстве стоит дифференциал функции, которую назовем функцией Лагранжа и обозначим через
![]()
Сама функция имеет вид
![]()
Исследуя функцию
на локальный экстремум, подберем один
из множителей
,
так, чтобы в некоторой точке ![]() было
выполнено равенство
было
выполнено равенство
![]()
Поскольку дифференциал функции
равен нулю, то ![]() также, причем
также, причем ![]() .
.
Таким образом, система
![]()
выражает необходимые условия локального
экстремума функции
.
Система содержит две переменные величины
![]() и два параметра
и
.
Для нахождения 4-х неизвестных добавим
уравнение связи
и два параметра
и
.
Для нахождения 4-х неизвестных добавим
уравнение связи ![]() и одно из равенств
и одно из равенств ![]() или
или ![]() .
.
Итак, условия первого порядка при нахождении локального экстремума функции Лагранжа и условного экстремума с обратной связью функции сформулированы:

Последнее условие можно заменить на
равенство
+
![]() ,
поскольку
,
поскольку
![]()
Из первых двух уравнений системы найдем
![]() ,
считая
,
считая ![]() и
и ![]()
![]() ,
,
что совпадает с равенством (14).
Перейдем к достаточным условиям условного экстремума с обратной связью. Возьмем дифференциал от обеих частей в уравнении связи
![]() ,
,
откуда, считая, что ![]() ,
найдем
,
найдем ![]()
![]()
Подставим выражение во второй дифференциал функции Лагранжа
![]() .
.
Преобразуя, получим
![]() .
.
Второй сомножитель в скобках переписываем как окаймленный гессиан
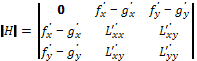 .
.
Его знак к критической точке указывает
на локальный минимум или максимум
функции ![]() ,
а, следовательно, на условный минимум
или максимум функции
:
,
а, следовательно, на условный минимум
или максимум функции
:
если ![]() то
то ![]()
если ![]() то
то ![]()
ПРИМЕР 1. Найти экстремум в системе функций
![]()
Решение. Функция Лагранжа задачи на условный экстремум с обратной связью имеет вид
![]() .
.
Найдем необходимые условия
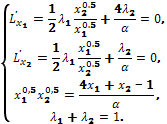
Разделив 1-е
уравнение на 2-е, получим ![]() Подставим в 3-е уравнение, будем иметь
Подставим в 3-е уравнение, будем иметь
![]() .
Для функции Кобба-Дугласа в стационарной
точке существует максимум. Его величина
.
Для функции Кобба-Дугласа в стационарной
точке существует максимум. Его величина
![]() На рис. 7.18 представлены условные максимумы
для трех значений
На рис. 7.18 представлены условные максимумы
для трех значений ![]() .
При при отсутствии обратной связи
.
При при отсутствии обратной связи ![]() получим стандартный условный экстремум
получим стандартный условный экстремум
![]() ,
точка
,
точка ![]() В случае положительной обратной связи
с коэффициентом
В случае положительной обратной связи
с коэффициентом ![]() имеем
имеем ![]() ,
точка
,
точка ![]() При отрицательной обратной связи с
коэффициентом
При отрицательной обратной связи с
коэффициентом ![]() максимум
максимум ![]() соответствует точке
соответствует точке ![]()
Если исследуемая функция не является дифференцируемой, метод Лагранжа не применим.
ПРИМЕР 2. Исследовать на экстремум функцию , заданную системой уравнений
![]()
Решение. Область значений функции . Найдем корни уравнения
![]() ,
,
для чего возведем его в квадрат
![]() .
.
П осле
сокращения уравнение примет вид
осле
сокращения уравнение примет вид
![]() .
Следовательно,
.
Следовательно,
![]() или
.
При
получим
или
.
При
получим
![]() .
Очевидно, минимальное значение
равно
.
Очевидно, минимальное значение
равно
![]() при
и
.
Другой случай
приводит к тому же результату. Отметим,
что
при
и
.
Другой случай
приводит к тому же результату. Отметим,
что
![]() представляет глобальный минимум
функции
.
На рис. 7.17 изображены графики функций
и
представляет глобальный минимум
функции
.
На рис. 7.17 изображены графики функций
и
![]() ,
Пересекающиеся по плоскостям
и
.
Линии пересечения поверхностей указаны
красным цветом.
,
Пересекающиеся по плоскостям
и
.
Линии пересечения поверхностей указаны
красным цветом.
Некоторые из функций системы могут быть заданы в неявном или параметрическом виде.
П РИМЕР
3. Исследовать на
экстремум функцию
,
заданную системой уравнений
РИМЕР
3. Исследовать на
экстремум функцию
,
заданную системой уравнений
![]()
Решение. Подставим
![]() в первое уравнение:
в первое уравнение:
![]() .
.
Представим уравнение как квадратное относительно :
![]() .
.
Его решение
![]()
подставим во второе уравнение системы. Получим
![]() .
.
Исследуем функцию
![]() на экстремум с помощью производной.
на экстремум с помощью производной.
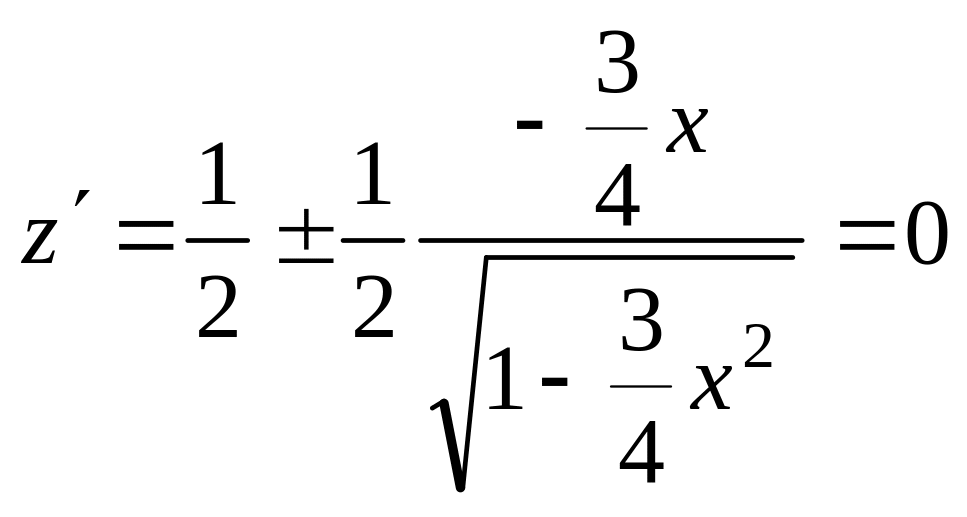 .
.
Уравнение ![]()
при
![]() имеет решение
имеет решение
![]() .
При
.
При
![]() решение
решение
![]() .
Исследование знаков производной
показывает, что в точке
достигается максимум
.
Исследование знаков производной
показывает, что в точке
достигается максимум
![]() ,
в точке
- минимум
,
в точке
- минимум
![]() .
.
Окончательно,
получаем ![]() ,
,
![]() .
.
Графики обеих функций представлены на рис. 7.20. Стрелками указаны минимум и максимум функции , причем минимум наблюдается, а максимум скрыт под поверхностью сферы. Для улучшения обзора из сферы удалена часть поверхности.
