139

Глава 7 Классические методы оптимизации

Глава 7. Классические методы оптимизации

Классические методы оптимизации построены на использовании как инструментов математического анализа (теория функций нескольких переменных), так и на аппарате линейной алгебры (матричная алгебра, векторная алгебра, квадратичные формы).

§7.1. Локальный экстремум

Определение локального экстремума Необходимые условия локального экстремума Достаточные условия локального экстремума Использование квадратичных форм

Определение локального экстремума

Пусть функция существует в некоторой области, и точка - внутренняя точка этой области.

Определение. Точка называется точкой локального максимума (минимума) функции , если существует окрестность точки такая, что для всех точек из этой окрестности ( ).

Определение можно интерпретировать в терминах приращений. Если приращение функции , соответствующее приращению аргументов и , в некоторой окрестности точки сохраняет знак, то точка является точкой локального максимума (минимума).

Значение функции в точке называется локальным максимумом или локальным минимумом функции. Точки максимума и точки минимума функции называются точками экстремума функции, а сами максимумы и минимумы функции – ее экстремумами.

Будем различать строгий экстремум (его условие или ) и нестрогий экстремум (условие или ). Например, функция имеет в точке строгий локальный минимум, равный нулю (рис. 7.1), а функция - нестрогий локальный минимум, равный нулю на линии (рис. 7.2).

Необходимые условия локального экстремума

(о необходимом условии экстремума)

Если - точка экстремума функции, то все частные производные в этой точке равны нулю либо не существуют.

◄ Пусть в точке функция имеет экстремум. Зафиксируем переменную , придав ей значение . Тогда функция будет функцией одной переменной по . Поскольку она имеет экстремум в точке , ее производная по , равная , обратится в нуль или не будет существовать. Подобным образом убеждаемся, что также равна нулю или не существует. ►

Следствие. Если - точка экстремума функции , то первый дифференциал функции равен нулю.

Следствие вытекает из определения дифференциала .

Е сли частные производные обращаются в нуль в точке , она может и не оказаться точкой экстремума. Например, функция имеет частные производные и , которые в точке равны нулю. Из графика (рис. 7.3) видно, что в точке , указанной стрелкой, минимума или максимума нет. Таким образом, необходимые условия не оказы­ваются достаточными.

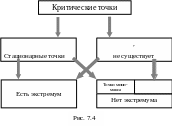
Точки, в которых производные , либо не существуют, называются критическими точками функции. Те из критических точек, в которых , , называются стационарными. Среди стационарных точек есть точки, в которых экстремум функции не достигается. Они называются седловыми точками или точками минимакса. На рис. 7.3 стрелкой указана подобная точка. На рис. 7.4 приведены возможные варианты с критическими точками.

Достаточные условия локального экстремума

Достаточные условия рассмотрим вначале для функции двух переменных, затем перейдем к общему случаю.

(об исследовании на экстремум по угловым минорам)

Пусть всюду в окрестности точки :

1. определена функция ;

2. непрерывны, причем , ;

3. непрерывны.

В этом случае угловые миноры

и

матрицы

определяют поведение функции в точке , причем:

1. если угловые миноры , , функция имеет в точке минимум;

2.если угловые миноры , , функция имеет в точке максимум;

3. если угловой минор , функция не имеет в точке экстремума.

◄ Разложим приращение функции в точке в ряд Тейлора до второго дифференциала включительно: .

В точке первый дифференциал . Поведение функции (ее приращение) определяется вторым дифференциалом. Слагаемое является бесконечно малым по отношению к . Поэтому можно выбрать столь малую окрестность точки , что знак будет определяться знаком в этой точке. Итак, если , то , т.е. при выходе из точки функция возрастает. В противном случае при будем иметь . Функция будет убывать при движении из точки .

Раскроем второй дифференциал

и вынесем за скобки, обозначив через . При вариации и в произвольных пределах переменная изменяется от до . Тогда

(1)

Выражение (1) представляет собой квадратный трехчлен, описывающий параболу. Поведение параболы определяется ее коэффициентом при квадрате неизвестной и знаком дискриминанта . Проведем это исследование.

1. При и квадратный трехчлен описывает параболу, направленную ветвями вверх и всю лежащую выше оси абсцисс. Это означает, что при второй дифференциал , следовательно, . Функция имеет в точке минимум.

2. При и квадратный трехчлен описывает параболу, направленную ветвями вниз и всю лежащую ниже оси абсцисс. Это означает, что при второй дифференциал , следовательно, . Функция имеет в точке максимум.

3. При выполнении условия в некотором интервале изменения часть параболы расположена выше оси абсцисс, для других значений часть параболы расположена ниже оси. Соответственно, при движении из точки в направлениях, для которых , т.е. дифференциалы и имеют одинаковый знак, будем иметь один знак . При движении в других направлениях, когда , а значит, дифференциалы и имеют разные знаки, получим другой знак . Экстремума нет.

Из вторых производных составим матрицу

.

Условия и означают, что угловые миноры , . В точке наблюдается минимум. Условия и , соответствующие максимуму, приводят к неравенствам , . Наконец, условие приводит к неравенству , означающему отсутствие экстремума. Теорема доказана. ►

Использование квадратичных форм

Для рассмотрения общего случая привлечем теорию квадратичных форм. Второй дифференциал функции нескольких переменных можно рассматривать как симметричную квадратичную форму относительно дифференциалов переменных. Ее частным случаем является второй дифференциал от функции двух переменных, рассмотренный выше. Второй дифференциал функции переменных имеет вид

.

Матрица этой квадратичной формы, составленная из вторых частных производных функции , называется матрицей Гессе^

.

Как и в случае двух переменных, приращение функции в точке возможного экстремума разложим в ряд Тейлора

.

Знак приращения при непрерывности частных производных до второго порядка включительно в точке и ее некоторой окрестности будет определяться знаком второго дифференциала, являющегося квадратичной формой. Условия знакоопределенности квадратич­ной формы формулирует как критерий Сильвестра. Напомним, что критерий Сильвестра основан на изучении знаков угловых миноров матрицы квадратичной формы. На основе этих рассуждений сформулируем теоремы.

( об исследовании на экстремум по второму дифференциалу)

Пусть всюду в окрестности точки :

1. определена функция ;

2. все частные производные первого порядка ,где , непрерывны, причем ;

3. все частные производные второго порядка , где , непрерывны;

4. второй дифференциал в точке является знакоопределенной квадратичной формой.

Тогда функция имеет в точке локальный экстремум, причем:

а) при - локальный минимум,

б) при - локальный максимум.

Если же является знакопеременной квадратичной формой в точке , то функция не имеет локального экстремума.

Дадим еще одну формулировку достаточных условий локального экстремума, удобную в использовании.

(об исследовании на экстремум по угловым минорам)

Пусть всюду в окрестности точки :

1. определена функция ;

2. все частные производные первого порядка ,где , непрерывны, причем ;

3. все частные производные второго порядка , где , непрерывны.

В этом случае угловые миноры , , …, матрицы Гессе определяют поведение функции в точке , причем:

1. если все угловые миноры положительны, функция имеет в точке минимум;

2. если знаки миноров чередуются начиная с отрицательного, функция имеет в точке максимум.

Замечание. Теорема дает достаточные условия локального экстремума. Угловые миноры не всегда могут помочь в исследовании функции на экстремум. Иначе говоря, эти достаточные условия не являются необходимыми. Например, функция имеет в точке строгий минимум, хотя не выполнено в силу равенства нулю в этой точке всех вторых производных. Для этой функции при любых и имеет место . Одну из идей нахождения экстремума в таких случаях рассмотрим ниже.

ПРИМЕР 1. Функцию исследовать на локальный экстремум.

Решение. Найдем критические точки функции:

Решениями системы являются коор­дина­ты двух точек: и .

Найдем вторые частные производные:

, ,

и составим из них матрицу Гессе:

.

1. Точка . . Экстремума нет.

2. Точка .

. Экстремум есть; . Следовательно, в точке функция имеет локальный максимум .

На рис. 7.5 приведен график функции . Синей стрелкой указано положение максимума функции, фиолетовой стрелкой – седловая точка (точка минимакса).

ПРИМЕР 2. Функцию исследовать на локальный экстремум.

Решение. Эту функцию мы уже рассматривали в замечании к теореме и обнаружили, что все вторые частные производные в стационарной точке равны нулю.

Обратимся непосредственно к приращению функции

,

которое в точке имеет вид

.

Очевидно, что при любых значениях и , таких, что , приращение

.

Функция имеет в точке минимум. На рис. 7.6 представлен график функции , на котором выделена точка минимума и стрелкой указано местонахождение этой точки.