Билет 15. Теорема о главных осях. Диагонализация тензора инерции. Главные моменты инерции твердого тела.

Теорема: Для любого тела и любой точки О существует три взаимоперпендикулярных направления, при вращении вокруг которых вектор момента импульса сонаправлен с вектором угловой скорости. Такие направления называются главными осями и для них , где

Билет 14. Момент импульса относительно точки. Связь между моментом импульса относительно точки и угловой скоростью вращения твердого тела. Тензор инерции.

Докажем, что момент импульса относительно оси- проекция импульса относительно точки на направление оси ( на примере точки)

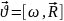
Билет 11. Аналогия между поступательным движением материальной точки и вращательным движением твердого тела.

Поступательное относительно точки	Вращательное движение твердого тела
S,	-угол
2. , ,
3.	-от-но точки, -от-но оси
4.
5.m
6.	-точки от-но точки, -тела от-но оси. - точки от-но оси
7.
8.
9.
10.

Билет 18. Законы Кеплера. Закон всемирного тяготения. Опыт Кавендиша.

Первый закон Кеплера (закон эллипсов)

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с окружностью характеризуется отношением  , где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.

Второй закон Кеплера (закон площадей)

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии. Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Доказательство второго закона Кеплера. По определению угловой момент   точечной частицы с массой m и скоростью   записывается в виде: .где   — радиус-вектор частицы а   — импульс частицы. Площадь, заметаемая радиус-вектором   за время dt из геометрических соображений равна  , где θ представляет собой угол между направлениями   и  . По определению

В результате мы имеем .Продифференцируем обе части уравнения по времени поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что  , а следовательно и пропорциональная ей скорость заметания площади   — константа.

Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

, где T₁ и T₂ — периоды обращения двух планет вокруг Солнца, а a₁ и a₂ — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:  , где M — масса Солнца, а m₁ и m₂ — массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Космическая скорость (первая v₁, вторая v₂, третья v₃ и четвёртая v₄) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет:

• v₁ — стать спутником небесного тела (то есть способность вращаться по орбите вокруг НТ и не падать на поверхность НТ).

• v₂ — преодолеть гравитационное притяжение небесного тела.

• v₃ — покинуть звёздную систему, преодолев притяжение звезды.

• v₄ — покинуть галактику.

Закон всемирного тяготения. Сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделёнными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть

:

Здесь G — гравитационная постоянная, равная   м³/(кг с²).

Опыт Кавендиша. Установка представляет собой деревянное коромысло с прикреплёнными к его концам небольшими свинцовыми шарами диаметром 5 см и массой 775 г. Оно подвешено на нити из посеребрённой меди длиной 1 м. К шарам подносят шары большего размера диаметром 20 см и массой 49,5 кг, сделанные также из свинца. В результате действия гравитационных сил коромысло закручивается на некий угол. Жёсткость нити была такой, что коромысло делало одно колебание за 15 минут. Угол поворота коромысла определялся с помощью луча света, пущенного на зеркальце на коромысле, и отражённого в микроскоп. Зная упругие свойства нити, а также угол поворота коромысла, можно вычислить гравитационную постоянную. Для предотвращения конвекционных потоков установка была заключена в ветрозащитную камеру. Угол отклонения измерялся при помощи телескопа. Заподозрив в качестве причины закручивания нити магнитное взаимодейстивие железного стержня и свинцовых шаров, Кавендиш заменил стержень медным, получив те же результаты.  Г. Кавендиш получил значение G=6,754×10⁻¹¹

Билет 10 . Кинетическая энергия вращающегося тела. Работа по повороту твердого тела.

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить: . Если тело вращается вокруг неподвижной оси с угловой скоростью  , то линейная скорость i-ой точки равна  , где  , - расстояние от этой точки до оси вращения. Следовательно. , где   - момент инерции тела относительно оси вращения. В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости   центра инерции тела, и вращения с угловой скоростью  вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду , где   - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

Работа по повороту твердого тела.

Рассмотрим действие внешней силы  , приложенной к точке массой  . За время   элементарная масса   проходит путь   Работа силы   на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей   силы. Но   равна модулю момента   силы   относительно оси вращения. Работа  , и будет положительна, если   имеет такое же направление, как и   отрицательное, если направление векторов   и   противоположны. С учетом, что  Работа всех сил, приложенных к телу

Полная работа

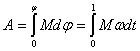
Билет 12. Момент инерции. Вычисление моментов инерции тел ( на примере моментов инерции цилиндра, кольца, тонкого кольца, стержня и шара)

Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами  , и моменты инерции тела определяется интегралом где  - расстояние от элемента   до оси вращения.

Распределение массы в пределах тела можно охарактеризовать с помощью плотности где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение дает среднюю плотность.

. Плотность в данной точке в этом случае определяется следующим образом и тогда

Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.

Момент инерции полого цилиндра с тонкими стенками, радиуса R.

Для полого цилиндра с тонкими стенками

Сплошной однородный диск. Ось вращения является осью диска радиуса  . и массы m с плотностью  Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки   и массой . Для него

Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:

Момент инерции шара относительно оси, проходящей через центр тяжести.

Момент инерции стержня длиной L и массой m относительно оси, проходящей:

а) через центр стержня - 

б) через начало стержня - 

Билет 13. Момент инерции. Теорема Гюйгенса-Штейнера.

Теорема Гюйгенса-Штейнера. Момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:  — известный момент инерции относительно известной оси,

 — искомый момент инерции,

 — масса тела,

 — расстояние между осями (известной и относительно которой необходимо найти момент инерции)

Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами  , и моменты инерции тела определяется интегралом где  - расстояние от элемента   до оси вращения.

Распределение массы в пределах тела можно охарактеризовать с помощью плотности где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение дает среднюю плотность.

. Плотность в данной точке в этом случае определяется следующим образом и тогда

Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела