§7.3. Экстремум неявной функции

Пусть функция определяется уравнением . Потребуем, чтобы функция была дважды непрерывно дифференцируема и .

Первый дифференциал в стационарной точке равен нулю:

,

что может иметь место в силу независимости дифференциалов и только при

(10)

Уравнения (10) выражают необходимые условия существования экстремума, определяя точку возможного экстремума. Для нахождения достаточных условий найдем второй дифференциал в стационарной точке .

. (11)

Найдем отдельно каждое из слагаемых в правой части равенства (11):

.

В стационарной точке , поэтому равенство значительно упростится

.

Аналогично можно доказать, что

.

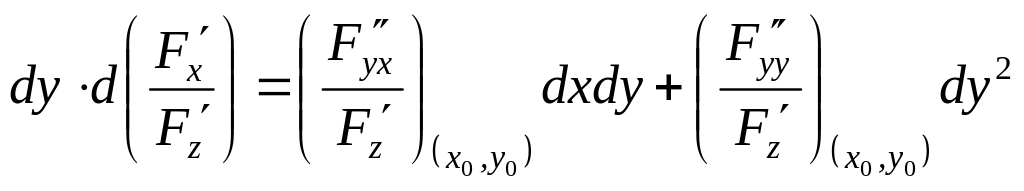Подставим полученные равенства в (11) и преобразуем квадратичную форму, используя :

. (12)

Матрица Гессе для квадратичной формы (12) примет вид

.

Применяя критерий Сильвестра к найденной матрице, исследуем знакоопределенность квадратичной формы и сделаем вывод о существовании экстремума неявной функции.

ПРИМЕР. Найти локальный экстремум неявной функции

в области , считая .

Решение. Найдем частные производные функции по всем переменным:

Чтобы определить стационарные точки, решим систему уравнений

Выразим переменную из первого уравнения и подставим во второе

Получим критические точки с координатами и с координатами . Подстановка этих значений аргументов в уравнение с учетом даст значения и . Итак, имеем и .

Найдем вторые частные производные: , , и составим матрицу Гессе квадратичной формы для неявной функции:

.

О бращаем внимание, что из матрицы можно вынести множитель 3, но нельзя вынести множитель , так как нужна информация о знаке первого углового минора . Рассмотрим вначале точку .

1. . Здесь , . В этой точке достига­ется локальный максимум, равный .

2. . Здесь . Поэтому обратимся ко второму дифференциалу.

.

Очевидно, не является знакоопределенной квадратичной формой. Поэтому в данной точке экстремума нет. На рис. 7.16 приведен фрагмент поверх­ности заданной неявной функции. Стрел­ками указаны точки и .

§7.4. Глобальный экстремум

Глобальным экстремумом называется наибольшее и наименьшее значения функции в замкнутой ограниченной области . Пусть функция непрерывна в этой области. Тогда найдется точка , в которой функция принимает наибольшее (наименьшее) значение. Если точка лежит внутри области , она является стационарной, и в ней может достигаться локальный максимум или минимум. Наибольшее или наименьшее значение функция может принимать также на границе области. Следовательно, задачу исследования функции на глобальный (global) экстремум в области можно сформулировать так:

Решение задачи разбивается на две части:

1) исследование функции на локальный (local) экстремум в области :

2) исследование функции на условный (conditional) экстремум на границе области :

Наибольшее (наименьшее) из всех этих чисел и будет искомым наибольшим (наименьшим) значением функции в области .

ПРИМЕР. Исследовать на глобальный экстремум функцию в области , , .

Решение. Для решения задачи

надо рассмотреть несколько случаев:

1 )

Находим стационарные точки . Единственная стационарная точка не входит в рассматриваемую область.

2)

Подставим выражение в исследуемую функцию. Получаем . Во всех точках окружности функция принимает одно и тоже постоянное значение .

3)

В силу симметрии задачи из двух случаев достаточно рассмотреть один, например, . Подставим в функцию : . Это парабола с ветвями, направленными вниз. Критическая точка , в которой функция принимает значение, равное . На концах отрезка функция равна .

4)

Система рассматривается аналогично случаю 3. Собираем все полученные значения функции :

Выбираем наибольшее и наименьшее значение из всех этих чисел:

.

График функции в области приведен на рис. 7.17.

Замечание. При исследовании функции на глобальный экстремум можно ограничиться отысканием значения функции в критических точках. Достаточные условия обычно не используют.

В математическом анализе существует класс так называемых выпуклых функций, примерами которых могут служить функции, представленные на рис. 7.6 - 7.8. Они широко применятся в экономике и в дальнейшем будут нами изучаться. Выпуклая функция не имеет седловых точек. Поэтому равенство ее частных производных нулю является не только необходимым, но и достаточным условием локального экстремума. Локальный экстремум выпуклой функции является также и глобальным, т.е. наибольшим значением функции в случае, когда функция выпукла вверх, и наименьшим, когда она выпукла вниз.