Доведення

Наближаємося до точки (0,0) по прямій y = kx.

Зауважимо, що значення границі залежить від кутового коефіцієнта прямої, наприклад:

при границя дорівнює

при границя дорівнює і т. д.

Отже, наближаючись до точки (0,0) у різних напрямах, дістаємо різні границі. Це означає, що не існує.

Відповідь. Доведено, що не існує.

Зауваження. Для функції змінних можна розглядати n! так званих повторних границь.

У частковому випадку для функції двох змінних z = f (x, y) можна розглядати дві повторні границі в точці (x₀, у₀):

Наприклад, для функції маємо:

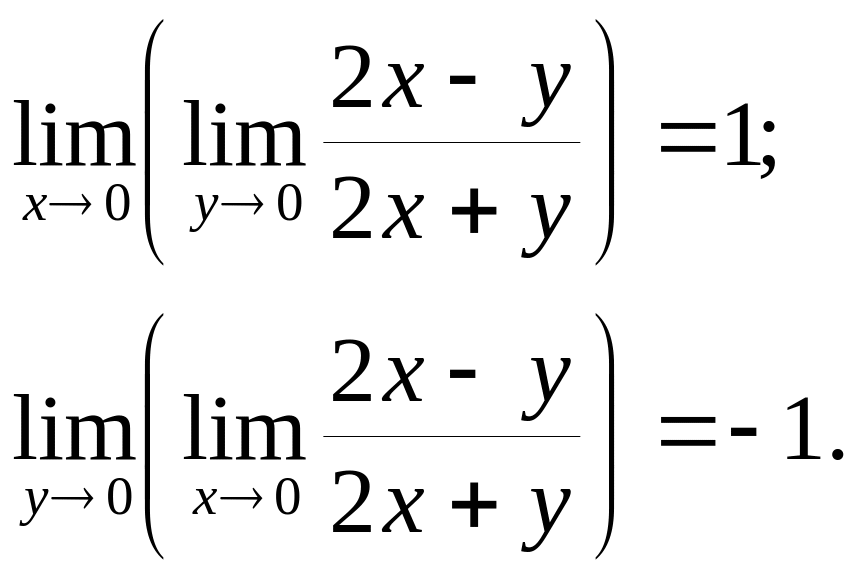
Отже, змінювати порядок граничних переходів загалом не можна.

Скажімо, у попередньому прикладі не існує, але повторні границі існують:

Неперервність функцій двох змінних

Означення. Функція z = f (x, y) називається неперервною в точці Р₀ (х₀, у₀), якщо:

Означення. Функція z = f (x, y) неперервною в області (замкненій чи відкритій), якщо вона неперервна в кожній точці цієї області.

Означення. Функцію z = f (x, y), визначену на множині , називають неперервною за множиною в точці , якщо:

Означення. Точка (x₀, у₀) називається точкою розриву функції z = f (x, y), якщо:

1. функція z = f (x, y) не визначена в точці (x₀, у₀);

2. функція z = f (x, y) не визначена в точці (x₀, у₀), проте:

• не існує;

• існує, але не дорівнює f (x₀, у₀)

Означення. Точка (x₀, у₀) називається точкою усувного розриву функції f (x, y), якщо існує, але або f (x, y) не визначена в точці (x₀, у₀), або

Неперервність складеної (складної) функції двох змінних

Означення. Нехай функція визначена на множині ,а змінні u і v, у свою чергу, залежать від змінних x і y: , причому обидві функції u(x, у) та визначені на множині D. Якщо для будь-якого існує значення , то говорять, що на множині визначено складену (складну) функцію де ; u, v - проміжні, х, у - незалежні змінні.

Наприклад, функція , де Це складена функція, яка визначена на координатній площині. Її можна записати у вигляді:

Теорема 1.5. Нехай на множині D визначено складену функцію , де і нехай функції неперервні в точці , а функція неперервна в точці , де Тоді складена функція неперервна в точці (x₀, у₀).

Приклади для самостійного розв’язування

1. Знайти області визначення та неперервності функцій:

а) ; б) ; в) .

2. Обчислити границі:

а) ; б) ;

в) ; г) .

3. Знайти розриви функції:

а) ; б) ; в) .

Найбільше та найменше зна­чення функції в замкненій обла­сті

Нехай дано функцію , яка неперервна на відрізку [a;b], диференційована в інтервалі (a;b), за винятком можливо скінченого числа точок, де вона не існує. Необхідно ж знайти найбільше та найменше значення функції на цьому відрізку. А як відомо з математичного аналізу, функція, яка неперервна на відрізку, набуває на ньому свого найбільшого і найменшого значення.

Чим викликана необхідність знаходження найбільшого і найменшого значення функції на відрізку?

Справа в тому, що в практичних задачах, де процес, явище, закон, величина описуються певною функцією, зміст самої задачі накладає певні обмеження на аргумент, тобто аргумент має певні межі.

Так, наприклад, кут трикутника може змінюватися лише від 0 до π, швидкість тіла доводиться розглядати в проміжку часу від t₀ до t₁ та інше. Тому й необхідно досліджувати поведінку функції на конкретному проміжку [a;b] або на його кінцях, то чинять так:

1. знаходять критичні точки в інтервалі (a; b) (точки, в яких похідна дорівнює нулю або не існує), обчислюють значення функції в цих точках;

2. знаходять значення функції на кінцях відрізка, тобто ;

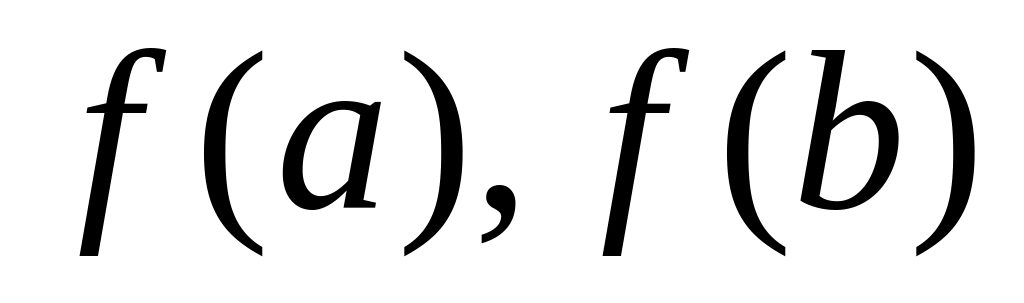3. серед усіх значень вибирають найбільше і найменше значення.

У випадку, коли функція монотонна на відрізку [a;b], то найбільшого і найменшого значення вона досягає на кінцях відрізка. У цьому випадку обмежуємось обчисленням значень .

По-іншому складається ситуація, якщо необхідно знайти найбільше та найменше значення функції, неперервної в інтервалі (a;b).

Зрозуміло, що функція у цьому випадку не може досягати найбільшого і найменшого значення на кінцях інтервалу. Наприклад, функція в інтервалі (3;6) не має ні найбільшого, ні найменшого значення у внутрішніх точках інтервалу. У цьому випадку чинять так:

1. знаходять критичні точки, що належать цьому інтервалу, і обчислюють значення функції в цих точках;

2. знаходять ліву та праву границі відповідно в точках а і b, тобто . Якщо ці границі існують, то їх порівнюють із значеннями функції в критичних точках. Якщо виявиться, що значення в критичних точках більші(менші) за знайдені границі, то це і буде найбільшим(найменшим) значенням функції на інтервалі.

Приклад. Знайти найбільше та найменше значення функції на відрізку [a;b].