1.3. Акустические волны в анизотропном упругом твердом теле

В анизотропном упругом твердом теле компоненты первого тензора Кристоффеля зависят от направления распространения волны. В соответствии с уравнениями квадрат фазовой скорости волны и вектор поляризации, являющиеся собственным зна­нием и собственным вектором первого тензора Кристоффеля, также зависят от направления распространения волны. В этом состоит одна из основных особенностей процесса распространения акустической волны в анизотропном твердом теле, которая значительно расширяет разнообразие свойств акустических волн в кристаллах по сравнению с изотропной средой.

Уравнения Кристоффеля для произвольного направления в кристалле содержат большое число слагаемых. Ввиду громоздких уравнений Кристоффеля основным методом их решения в на стоящее время является численный (реализуемый с помощью ЭВМ). В общем виде процесс решения заключается в следующем.

Задавшись направлением распространения волны 1, определяем с помощью соотношения компоненты первого тензора Кристоффеля 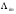для рассматриваемого кристалла и направле­ния. (Если направление распространения волны не совпадает с направлением осей системы координат установки кристалла, в которой заданы значения компонент тензора модулей упругости, то их предварительно необходимо пересчитать к соответствующей повернутой системе координат.) Затем находят собственные значения и собственные векторы первого тензора Кристоффеля, значения квадратов фазовых скоростей и векторов поляризации волны для заданного направления.

В общем случае тензор Кристоффеля обладает тремя различными собственными значениями, каждому из которых соответствует свой собственный вектор. Все три собственных вектора всегда взаимно перпендикулярны. При этом они могут не совпадать с направлением распространения волны. Однако в любом случае угол между вектором поляризации и волновой нормалью для данной из волн будет меньше, чем для двух остальных. Такая волна называется квазипродольной, а две другие—квазипоперечными. Взаимная перпендикулярность собственных векторов следует вещественности, симметричности и положительной определенно первого тензора Кристоффеля. При анализе свойств акустических волн следует иметь в виду, что для отдельных направлений тензор Кристоффеля может оказаться одноосным (два его собственных значения совпадут). В этом вырожденном случае две из трех волн будут иметь одинаковые фазовые скорости, а их векторы смещения могут иметь произвольное направление в плоскости, перпендикулярной вектору смещения третьей волны. Вдоль таких направлений, называемых акустическими осями, наряду с линейно поляризованными акустическими волнами могут распространяться и волны эллиптической поляризации. Как показывает анализ, в этом случае при определенных условиях имеет место явление внутренней конической рефракции акустической волны заключающееся в том, что одной и той же волновой нормали соответствует целый конус направлений вектора потока энергии, каждое из которых отвечает определенному вектору смещения квазипоперечной волны. В направлениях, не совпадающих с акустическими осями, волны, в общем случае, не являются ни чисто продольными, ни чисто поперечными.

В кристаллах существуют направления, свои для каждого типа симметрии кристалла, вдоль которых нормаль к фронту волны совпадает с вектором смещения для одной из трех волн, оказывающейся в таком случае чисто продольной. Такое направление называется продольной нормалью. В силу ортогональности векторов смещения две другие волны окажутся в этом случае чисто поперечными. В зависимости от симметрии рассматриваемого правления эти поперечные волны могут иметь различные или одинаковые скорости распространения.

Для некоторых направлений в кристаллах может оказаться, что только одна из трех волн является чисто поперечной. Такое направление называется поперечной нормалью. При распространении волны в этом направлении угол между вектором поляризации квазипродолыюй волны и волновой нормалью будет paвен углу между вектором поляризации квазипоперечной волны и плоскостью волнового фронта. Возможность существования квазипро­дольных и квазипоперечных объемных волн является еще одной особенностью распространения акустической волны в анизотроп­ном звукопроводе.

Наконец, третьей важной, с точки зрения практического ис­пользования акустических волн, особенностью, связанной с анизо­тропией свойств звукопровода, является отклонение потока энер­гии волны от направления ее распространения. Как уже отмеча­лось, этот эффект — весьма существенный, так как угол между векторами р и q (ср. 1.14) может достигать нескольких десятков градусов. Только в исключительных случаях отклонение потока энергии отсутствует. В частности, так случается при распростране­нии волны вдоль продольной нормали. Волну, у которой направ­ление лучевой скорости совпадает с волновой нормалью, иногда называют обыкновенной.

На практике часто нет необходимости находить вектор потока энергии, а достаточно знать только его направление. Для определения направления вектора потока энергии можно воспользоваться зависимостями фазовых скоростей от направления распростра­нения волны, известными из решения уравнений Кристоффеля. В [12] доказано, что направление потока энергии при заданном направлении распространения волны совпадает с направлением нормали к поверхности обратных значений фазовых скоростей (поверхности “медленности”) в точке, соответствующей этому направ­лению. Поверхность медленности образуется концами радиус-векторов, длины которых в каждом направлении равны обратному значению фазовой скорости волны, распространяющейся в данном направлении. Для объемных волн задача отыскания направления —потока энергии путем определения направления нормали к поверхности медленности является пространственной. Направления, вдоль которых распространяются обыкновенные волны (их часто называют направлениями чистых мод), можно найти непосредственно из угловых зависимостей фазовых скоростей, поскольку экс­тремумы угловых зависимостей фазовых скоростей и обратных им величин, очевидно, совпадают. Многочисленные примеры сечений поверхностей медленности приведены, в частности в книгах.

Переходя к анализу дифракционных эффектов в анизотропном ( упругом полубесконсчном звукопроводе, отметим, что в общем виде задача о поле излучения, создаваемого плоским жестким порш­нем ограниченных размеров, причем картина дифракции нуждается в индивидуальных расчетах для каждого выбранного направления конкретного кристалла. Для большинства практически важных случаев достаточно воспользоваться более универсальными результатами, которые относятся к направлениям, вблизи которых фазовая скорость и описывается параболической зависимостью

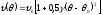(1.29)

где 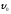—фазовая скорость вдоль исходного направления; у—па­раметр анизотропии; —угол отклонения исследуемого на­правления от исходного.

Такое приближение хорошо выполняется для осей высокой симметрии во всех типах кристаллов. В параболическом прибли­жении картина дифракции в анизотропном теле оказывается по­добной картине дифракции в изотропном теле. При этом в за­висимости от величины параметра анизотропии расстояние до границы зоны Френеля либо уменьшается (при у>0), либо уве­личивается (при —1<у<0), т. е. весь процесс дифракции либо “убыстряется” (при у>0), либо “замедляется” (при у<0) по сравнению с изотропным случаем (см. рис. 1.3,а и 1.4).

Анизотропия сказывается на свойствах не только объемных, но также и поверхностных акустических волн, фазовые скорости, век­торы поляризации и сама структура которых зависят от выбран­ного направления распространения. В частности для всех, за ис­ключением изолированных, направлений имеет место отклонение потока энергии от направления распространения волны. В настоя­щее время принято считать, что не существует запрещенных направлений распространения ПАВ ни для каких плоскостей крис­таллов. На свободной поверхности кристалла, наряду с релеевской волной со структурой, характерной для изотропного тела, могут существовать также обобщенные поверхностные волны и псевдоповерхностные волны. (Иногда в литературе под обобщенной по­верхностной волной понимают поверхностную волну, для которой единственное отличие от рэлеевской заключается в “осциллирую­щем” характере зависимости амплитуды смещений от глубины, однако, на наш взгляд, использование специального назва­ния для такого редко встречающегося изолированного типа вол­ны, неоправданно.)

Обобщенная поверхностная волна, в отличие от, релеевской, может иметь три компоненты смещений, а затухание смещения с глубиной может происходить по более сложному экспоненциаль­но-тригонометрическому закону.

Псевдоповерхностная волна, представляющая собой, по су­ществу, квазипоперечную объемную волну, имеет три компонен­ты смещения с преобладанием поперечной компоненты, лежащей в плоскости свободной поверхности. Ее волновой вектор лежит в сагиттальной плоскости, но наклонен под небольшим углом к по­верхности. В связи с этим псевдоповерхностную волну называют также скользящей или “мелкой” объемной волной. Строго говоря, псевдоповерхностная волна не является поверхностной в смысле- удовлетворения условию (1.28), она существует только в опреде­ленной области вблизи источника, превращаясь затем в объемные волны, по мере того, как поверхностная компонента теряет энер­гию за счет излучения объемной волны. Псевдоповерхностная вол­на существует вблизи изолированного направления распростране­ния обобщенной поверхностной волны, фазовая скорость распро­странения в котором превышает фазовую скорость наиболее медленной поперечной объемной волны, вследствие чего поверхност­ная волна начинает излучать энергию в объем. Псевдоповерхно­стные волны имеют сравнительно небольшой коэффициент погло­щения. Они в меньшей степени, нежели ПАВ, чувствительны к процессам старения поверхности, а также к качеству ее обработ­ки Найдены направления распространения псевдоповерхностных волн, для которых температурный коэффициент скорости и угол отклонения потока энергии малы, а коэффициент электромехани­ческой связи и скорость— велики. Все это, а также сравнительно высокая степень мономодности, способствуют все более широко­му применению псевдоповерхностных волн в акустоэлектронных устройствах.

Анализ отклонения потока энергии ПАВ в тех случаях, когда достаточно только сведений об угле 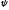между вектором потока энергии и волновым вектором, существенно проще, чем анализ от­клонения потока энергии объемной волны. Это связано с тем, что поверхности медленности для ПАВ цилиндрические, вследствие чего задача об отыскании нормалей к этим поверхностям стано­вится двумерной, а не трехмерной, как в случае объемных волн.

Проще оказывается и анализ дифракционных эффектов. Для ПАВ численный метод позволяет найти акустическое поле синфазно колеблющегося линейного излучателя вдоль произвольного направления в подложке любой симметрии. Однако результаты расчетов относятся только к одному конкретному направлению распространения ПАВ в кристалле заданной симметрии. Более универсальные, полезные для практики результаты удается полу­чить с помощью уже упоминавшегося параболического приближе­ния, в котором справедлива аппроксимация угловой зависимости фазовой скорости выражением (1.29).

Перейдем теперь к рассмотрению процесса поглощения акус­тических волн. Общая теория распространения акустических волн в релаксирующих средах, основанная на подходе, развитом Ман­дельштамом и Леонтовичем, показывает, что в рассматриваемом феноменологическом приближении 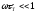(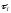-время релакса­ции фононного газа), выражение для коэффициента поглощения акустической волны, рассчитанного на единицу длины Г, имеет вид

(1.30)

где С — некоторый постоянный коэффициент, определяемый кон­кретным механизмом релаксации. Таким образом, величина Г при 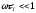пропорциональна квадрату частоты акустической волны.

Основным механизмом релаксации при распространении акус­тической волны, для которой 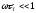, как впервые указал Ахиезер, является изменение спектра фононов, обусловленное деформацией кристаллической решетки. Это подтверждается, в частности, хо­рошим согласием расчетных и измеренных значений Г для моно­кристаллов, у которых детально исследованы свойства фононного спектра. Однако простая и надежная общая методика расчета ве­личины Г в настоящее время отсутствует. В связи с этим основ­ным способом получения наиболее важной для практики информации о минимально достижимых значениях Г остаются измере­ния.

Для оценок величины Т удобно пользоваться следующим при­ближенным выражением, соответствующим ахиезеровскому меха­низму поглощения:

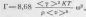
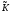где <у>—усредненный параметр Грюнайзена, определяемый из измерений теплопроводности; —коэффициент теплопроводности;

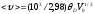—средняя скорость звука в дебаевском приближении, 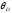— характеристическая температура Дебая, V₀- средний объем, приходящийся на один атом элементарной ячейки кристаллической решетки.

Полезными являются также различные попытки систематизации данных для кристаллов определенных классов, в частности система данных по поглощению акустических волн в кубических кристаллах, развитая в работе. В рамках этой системы вели­чина Г/f², определяемая экспериментально, сопоставляется со зна­чениями параметра

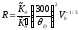(1.32)

где 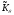—коэффициент теплопроводности при температуре Дебая;, М - средняя масса, приходящаяся на один атом вещества. Как видно из рис. 1.8, ре­зультаты измерения Г для большого числа кубических 'кристал­лов расположены в области между прямыми, соответствующими <у>==0,6 и <у>=1,2. Методика экспериментального опреде­ления Г достаточно подробно описана в работе.

Выше были представлены величины поглощения акустических волн для чистых материалов. Следует подчеркнуть, что они могут быть заметно уменьшены путем введения в монокристалл соот­ветствующим образом подобранных примесей. Особенно эффективного уменьшения затухания достигли при легирова­нии алюмоиттриевого граната примесями парамагнитных ионов. В этом случае величина Г при 10 ГГц снижалась с 30 до 15 дБ/мкс, что меньше величины Г (21 дБ/мкс) в AL₂O₃-материале, который наиболее часто применяется для изготовления акустиче­ских линий задержки (АЛЗ) гигагерцевого диапазона частот Вы­яснение предельных возможностей снижения коэффициента зату­хания за счет легирования кристаллов имеет большое практиче­ское значение для создания новых материалов для акустоэлек-тронных устройств с улучшенными параметрами.

Как показывает анализ, коэффициент поглощения попе­речной волны хорошо коррелирует с коэффициентом поглощения ПАВ. При этом необходимо отметить, что существующая техноло­гия обработки поверхности кристаллов позволяет практически полностью исключить влияние дефектов обработки поверхности на процесс поглощения ПАВ, по крайней мере до частот 3 ГГц.

Однако при оценке затухания ПАВ следует иметь в виду, что его величина более сложным образом зависит от частоты:

Здесь коэффициент А определяется только параметрами материала а коэффициент В — параметрами материала и окружающей

реды и может быть уменьшен при использовании легких газов или вакуумировании поверхности звукопровода.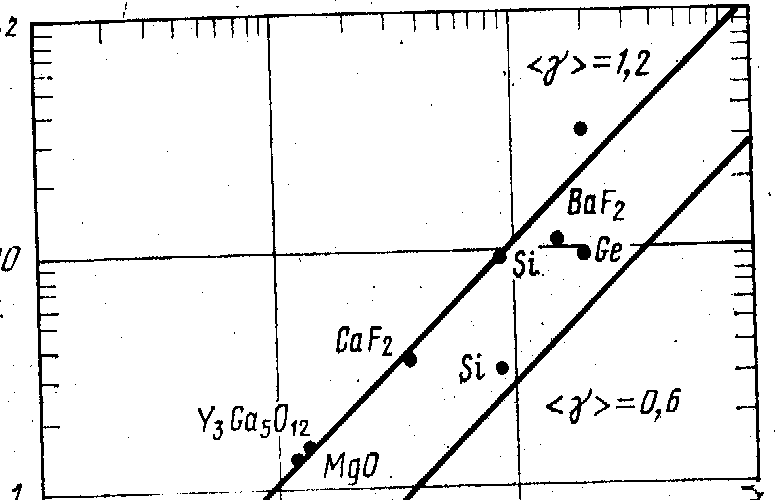

Рис. 1.8. Сопоставление величины Г-/-² с рас­четным параметром R для ряда кубических монокристаллов