
- •Акустические волны в твердом теле
- •1.2. Акустические волны в изотропном твердом теле.
- •1.3. Акустические волны в анизотропном упругом твердом теле
- •2. Возбуждение и прием акустических волн
- •2.2. Методы возбуждения (приема) поверхностных акустических волн
- •3. Акустические измерения
- •4. Полное звуковое поле в помещении при диффузном поле отражённого звука.
- •5. Акустические поверхностные волны в пьезоэлектрических кристаллах.
Акустические волны в твердом теле
1.АКУСТИЧЕСКИЕ ВОЛНЫ В ТВЕРДОМ ТЕЛЕ 1
1.1. ОБЩИЕ СВЕДЕНИЯ 1
1.2. АКУСТИЧЕСКИЕ ВОЛНЫ В ИЗОТРОПНОМ ТВЕРДОМ ТЕЛЕ. 6
1.3. АКУСТИЧЕСКИЕ ВОЛНЫ В АНИЗОТРОПНОМ УПРУГОМ ТВЕРДОМ ТЕЛЕ 13
2. ВОЗБУЖДЕНИЕ И ПРИЕМ АКУСТИЧЕСКИХ ВОЛН 22
2.1. ВОЗБУЖДЕНИЕ (ПРИЕМ) ОБЪЕМНЫХ АКУСТИЧЕСКИХ ВОЛН 22
2.2. МЕТОДЫ ВОЗБУЖДЕНИЯ (ПРИЕМА) ПОВЕРХНОСТНЫХ АКУСТИЧЕСКИХ ВОЛН 28
3. АКУСТИЧЕСКИЕ ИЗМЕРЕНИЯ 31
4. ПОЛНОЕ ЗВУКОВОЕ ПОЛЕ В ПОМЕЩЕНИИ ПРИ ДИФФУЗНОМ ПОЛЕ ОТРАЖЁННОГО ЗВУКА. 33
5. АКУСТИЧЕСКИЕ ПОВЕРХНОСТНЫЕ ВОЛНЫ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ. 34
1.1. ОБЩИЕ СВЕДЕНИЯ
Для описания процессов распространения акустических волн в диапазоне частот, используемых в современных акустоэлектронных устройствах, можно ограничиться феноменологическим приближением, при котором пренебрегают дискретностью атомной структуры и рассматривают твердое тело как непрерывную сплошную среду, поскольку длины акустических волн даже на частотах порядка 10 ГГц, по крайней мере, в 100 раз превышают межатомные расстояния.
При
обычно используемых интенсивностях
акустических волн применимо линейное
феноменологическое приближение, в
соответствии с которым вектор смещения
представляет собой линейную функцию
радиус-вектора рассматриваемой точки
в недеформированном состоянии r.
Коэффициенты этой линейной функции для
всех точек элементарного объема равны
значениям компонент тензора деформации
uik
относящимся к одной точке элементарного
объема. Компоненты тензора
uik
имеют вполне определенный геометрический
смысл: диагональные компоненты
(i=k)
представляют собой величины
относительных удлинений линейных
элементов, параллельных по деформации
осям
Oxi,
а недиагональные компоненты
(i k)
—
меру изменения углов между пересекающимися
прямыми до деформации, параллельными
осям Охi
и
Oxk.
k)
—
меру изменения углов между пересекающимися
прямыми до деформации, параллельными
осям Охi
и
Oxk.
При
анализе сил и динамики процессов в
деформируемом твердом теле в
феноменологическом приближении,
естественно, следует пренебрегать
радиусом действия атомных и молекулярных
сил, т. е. считать, что силы, действующие
на любой элемент объемa
со стороны соседних с ним частей,
действуют только через поверхность,
ограничивающую рассматриваемый элемент
объема. Помимо этих внутренних сил, ко
всем точкам могут быть также приложены
объемные силы, например сила тяжести.
Однако, как показывают оценки, действием
объемных сил при распространении
акустических волн можно пренебречь.
Поверхностные силы характеризуются
вектором напряжений—направлением и
значением нагрузки, действующей на
единицу площади выделенного сечения.
Вектор напряжения зависит от ориентации
выбранного сечения из связи с этим не
может использоваться в качестве величины,
однозначно характеризующей поверхностные
силы, действующие в точке. Для полного
описания поверхностных сил вводят
понятие
тензора
напряжения
 —совокупности
трех векторов напряжения в выбранной
точке, действующих по трем ортогональным
плоскостям, в качестве которых удобно
принять координатные плоскости
прямоугольной системы координат.
Общепринятые положительные направления
векторов напряжения, действующих по
граням элементарного параллелепипеда,
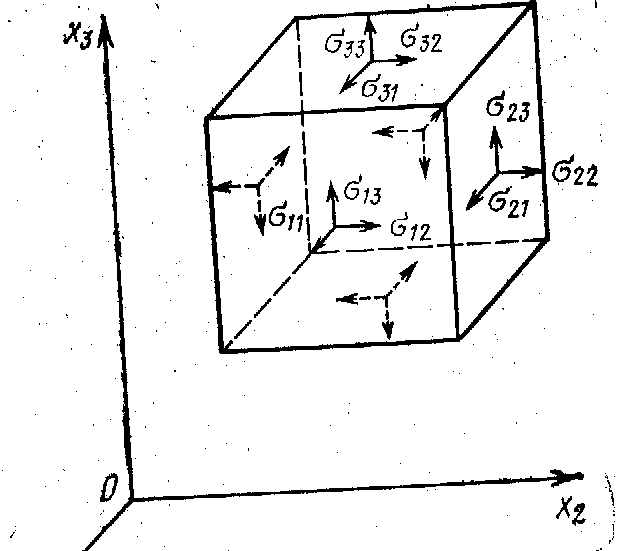
показаны на рис. 1.1. Процессы изменения
напряжений и смещений в сплошной среде
подчиняются второму закону Ньютона:
—совокупности
трех векторов напряжения в выбранной
точке, действующих по трем ортогональным
плоскостям, в качестве которых удобно
принять координатные плоскости
прямоугольной системы координат.
Общепринятые положительные направления
векторов напряжения, действующих по
граням элементарного параллелепипеда,
показаны на рис. 1.1. Процессы изменения
напряжений и смещений в сплошной среде
подчиняются второму закону Ньютона:
 (1.1)
(1.1)
Одних уравнении движения (1.1) недостаточно для однозначного описания процессов в сплошной среде. Недостающие соотношения, называемые материальными уравнениями находят из принципов термодинамики. Учитывая, что при распространении акустических волн малой интенсивности, обычно используемых в акустоэлектронных устройствах, происходят лишь малые отклонения от исходного равновесного состояния, для получения материальных уравнений ограничиваются линейным приближением.
Рис. 1.1. Положительные направления компонент тензора напряжений
В линейном приближении материальные уравнения для пъезодиэлектриков могут быть записаны в следующих двух эквивалентных формах в зависимости от выбранных независимых переменных
![]()

где
—
компоненты тензора диэлектрической
проницаемости
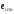 —компоненты
тензора пьезоэлектрических постоянных,
cikts-компоненты
тензора модулей упругости;
hirm—компоненты
тензора пьезоэлектрической константы
деформации.
—компоненты
тензора пьезоэлектрических постоянных,
cikts-компоненты
тензора модулей упругости;
hirm—компоненты
тензора пьезоэлектрической константы
деформации.
Для отдельных материалов некоторые коэффициенты уравнений могут быть либо тождественно равными нулю либо пренебрежимо малыми. Простейшее материальное уравнение называется законом Гука:
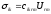 (1-4)
(1-4)
Подставляя в (1.1), получим уравнения движения в упругой среде. В акустоэлектронных устройствах, как правило, используются плоские гармонические волны, смещения в которых имеют вид
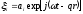 (1.5)
(1.5)
где
ai—компоненты
вектора поляризации;
q=2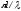 —волновой
вектор; l-единичный
вектор;
—волновой
вектор; l-единичный
вектор;
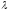 и
и
 -длина
и угловая частота
-длина
и угловая частота
волны; j—мнимая единица.
Для плоской волны уравнения движения в упругой среде принимают вид
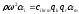 (1-6)
(1-6)
или в другой форме
 (1.7)
(1.7)
где
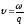 —скорость
акустической волны;
—скорость
акустической волны;
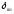 —
символ Кронекера;
—
символ Кронекера;
 (1.8)
(1.8)
—первый тензор Кристоффеля. Уравнения (1.7) носят название уравнений Кристоффеля. Они показывают, что задача о распространении плоской гармонической волны в упругом твердом теле сводится к нахождению собственных значений и собственных векторов первого тензора Кристоффеля.
При анализе процесса распространения плоской волны в пьезодиэлектрике необходимо совместно решать уравнения движения (1.1), материальные уравнения (1.2) или (1.3) и уравнения Максвелла. Однако детальный анализ показывает, что уравнения Максвелла при этом могут быть заменены уравнениями электростатики (возникающая ошибка по порядку величины равна квадрату отношения скорости акустической волны к скорости света). С учетом этого обстоятельства уравнения, описывающие распространение плоской волны в пьезодиэлектрике, имеют вид
 (1.9)
(1.9)
где
 при
i,r,s,m=1,2,3;
при
i,r,s,m=1,2,3;
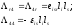 (1.10)
(1.10)
Cравнение систем уравнений (1.6) и (1.9) показывает, что задача о распространении плоской акустической волны в пьезодиэлектриках сложнее аналогичной задачи для упругого твердого тела, с математической точки зрения обе задачи однотипны и сводятся к решению систем однородных линейных уравнений.
Рассмотрим также важный для конструирования акустоэлектронных устройств вопрос о векторе потока энергии плоской акустической волны. Выражение для усредненной по времени величины вектора потока энергии плоской волны, справедливое для упругого тела и с достаточным приближением для известных пьезоэлектриков, имеет вид
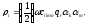 (1.11)
(1.11)
Эту величину часто называют также интенсивностью акустической волны. Отношение р к среднему значению плотности энергии волны называется вектором лучевой скорости s-Для плоской волны (1.5) имеем
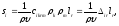 (1.12)
(1.12)
где тензор
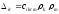 (1.13)
(1.13)
носит
название второго тензора Кристоффеля:
Направления век торов р
и
q
в упругой среде совпадают только в том
случае, когда q
является собственным вектором второго
тензора Кристоффеля. За исключением
этого случая оба вектора имеют различные
направления. Угол
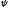 между ними, называемый углом отклонения
потока энергии, определяется выражением
между ними, называемый углом отклонения
потока энергии, определяется выражением
 (1.14)
(1.14)
Явление отклонения потока энергии акустической волны от направления ее распространения необходимо учитывать при конструировании акустоэлектронных устройств, так как углы реально могут составлять десять градусов, и более.
