1.2. Акустические волны в изотропном твердом теле.

Рассмотрение процессов распространения акустических волн в изотропном теле с точки зрения расчета параметров акустоэлектронных устройств имеет, в основном, методическое значение, так как коэффициент поглощения в реальных материалах с изотропными свойствами значительно выше, чем в лучших имеющихся монокристаллах (см. приложение Л, которое составлено по данны оригинальных и обзорных работ, опубликованных преимущественно в посленес время). Однако такое рассмотрение принципиально важно для полного решении задачи о распространении акустической волны.

В однородном изотропном твердом теле первый тензор Кристоффеля принимает особенно простой (диагональный) вид при совпадении направления распространения волны с одной из осей системы координат. Для определения предположим, что такой осью является ось Оху. В этом случае

(1.15)

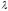где и — коэффициенты Ламэ. Уравнения Кристоффеля (1.7), решения и которых исчерпывают все виды акустических волн, распространяющихся в объёме тела (такие волны называются объемными), распадаются на три независимых уравнения:

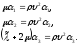(1.16)

Первые два (совпадающие) уравнения (1.16) описывают распространение объёмных акустических волн в которых смещения частиц перпендикулярны направ­лению распространения волны. Такие волны (рис. 1.2, а) называют поперечными (иногда сдвиговыми). Третье уравнение (1.16) описывает волну, в которой размещения частиц параллельны направлению распространения. Такие волны (рис.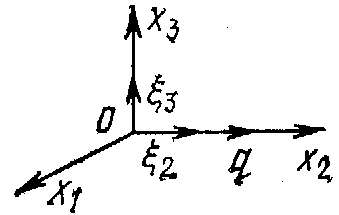

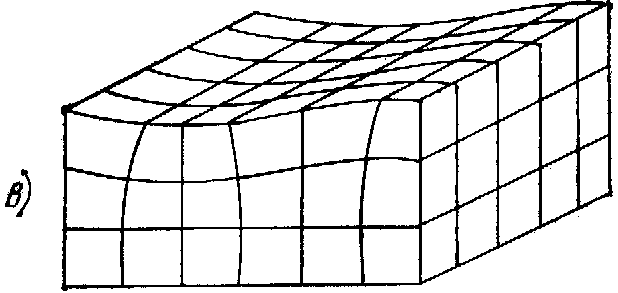
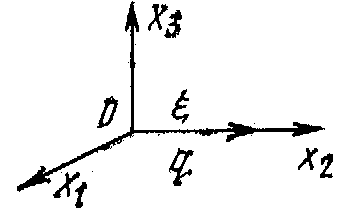
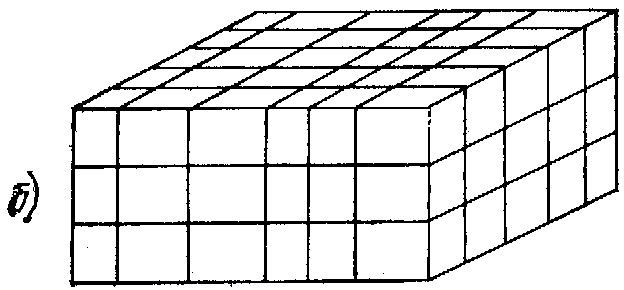
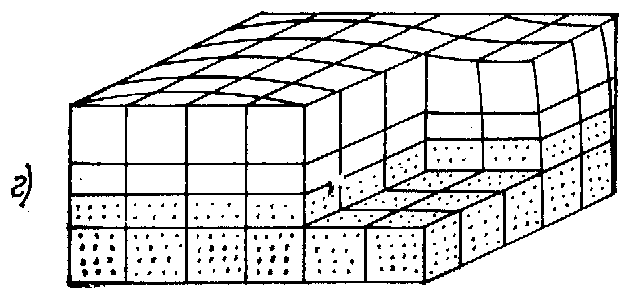
1.2,6) называют продольными (реже волнами сжатия). Оба указанных типa воли существуют и при произвольном направлении распространения, не совпадающем ни с одной из осей выбранной системы координат. Скорости распространения поперечной и продольной vi волн, как следует из (1.16), выража­лся следующими соотношениями:

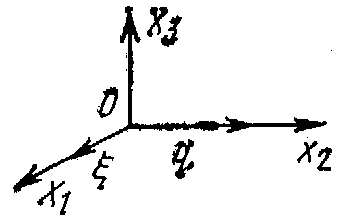
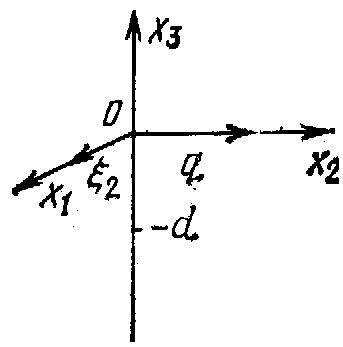
Рис. 1.2. Основные типы акустических волн в изотропном твердом теле

i — поперечная объемная волна; б — продольная Объемная волна; в — по­верхностная волна Релея; г — волна Лява

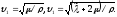(1.17)

С учетом реальных свойств известных изотропных материалов считаем 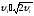.Вычисляя компоненты векторов лучевой скорости и потока энергии для поперечной и продольной волн в изотропной среде с помощью соотношений (1.11) и (1.12), найдем

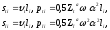(1.18)

где — акустический импеданс среды, который, как известно определяет отношение амплитуд давления к колебательной скорости 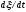.Соотношения (1.18) показывают, что в изотропном теле направление вектора лучевой скорости (потока энергии) поперечной и продольной воли совпадает с направлением их распространения.

До сих пор описывалось распространение объемных акустических волн t в бесконечном, однородном изотропном твердом теле. В реальных акустоэлектронных устройствах фронт волны ограничен в поперечных направлениях и ограничены линейные размеры звукопровода.

Проанализируем следствия этих ограничений. Обычно удается реализовать условия (при которых ограничением линейны) размеров звукопровода можно пренебречь. Ниже мы уточним, когда такое представление справедливо. В связи с этим целесообразно рассмотреть задачу в акустическом поле, создаваемом излучателем ограниченных размеров в полу бесконечном изотропном полупространстве. Будем считать, что поперечные размеры излучателя намного превышают длину акустической волны, что согласуется с практикой, а сам излучатель имеет вид жесткого поршня, все точки которого колеблются синфазно. Несмотря на сильно упрощенный характер такой модели излучателя, она позволяет получить достаточно хорошее согласие с экспериментальными данными, причем влияние формы излучателя оказывается очень существенным. Как показывает анализ, задача о поле излучения круглого жесткого поршня, даже в такой упрощенной постановке, не решается аналитически и может быть решена лишь численным методом. Из результатов расчетов следует, что вблизи излучателя существует зона Френеля, в которой волна имеет практически плоский фронт, а давление на оси проходит ряд пулев!. точек по мере удаления от излучателя (рис. 1.3). Вдали от излучателя давление на оси уменьшается обратно прапорционально расстоянию от излучателя и пучок акустической волны начинает расходиться, причем синус угла расхождения Ф удовлетворяет условию sinФ=0,31D_и

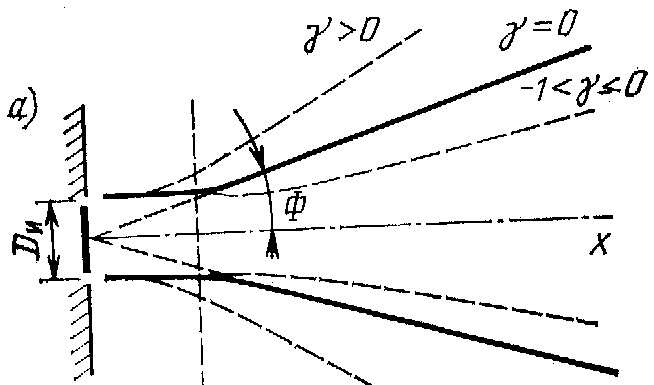
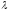, где D_и - диаметр излучателя. Эта зона называется зоной Фраунгофера. Граница между зонами Френеля и Фраунгофера, иногда называемыми также ближней и дальней зонами, не резкая. Условно считают, что она расположена на расстоянии 0,75D²_и/.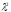

До сих пор рассматривалось лишь акустическое поле на оси излучателя, называемое главным лепестком диаграммы направленности излучателя. При больших углах между направлением распространения и осью излучателя имеют­ся направления, вдоль которых также возможно излучение акустической волны (боковые лепестки диаграммы направленности излучателя). Строго говорить о формировании лепестков диаграммы направленности излучателя можно толь­ко в зоне Фраунгофера.

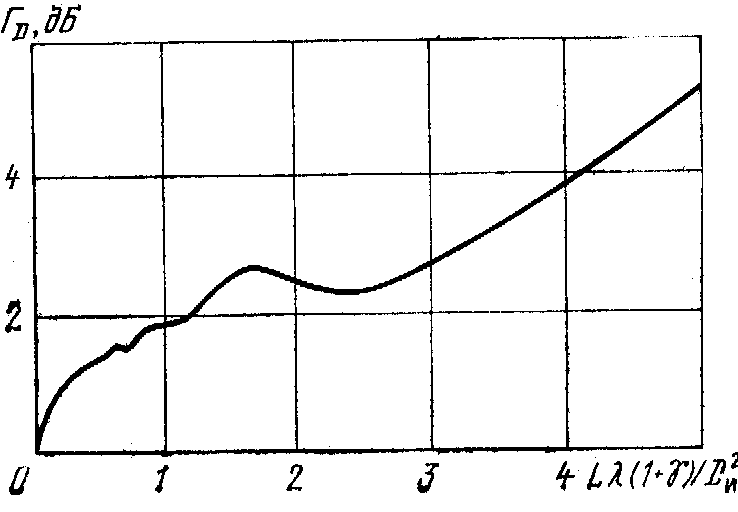
На рис. 1.4 приведен график, характеризующий потери акустической мощ­ности при распространении акустической волны в изотропной среде без погло­щения из-за дифракционного расширения фронта волны Го в зависимости от нормализованного расстояния между идентичными излучателем и приемником, представляющими собой жесткие круглые поршни. Этим графиком часто пользуются при расчете параметров акустоэлектронных устройств, использую­щих объемные волны.

Рис. 1.4. Зависимость дифракционных потерь объёмных волн от нормализованного расстояния между преобразователями.

L-расстояние между преобразователями; -длина акустической волны;D_и-диаметр излучателя; -параметр анизотропии материала звукопровода.

Описанная картина акустического поля излучателя с конечной апертурой, расположенного на границе полубесконечной среды, позволяет физически обо­снованно рассматривать вопрос о влиянии ограниченности поперечных размеров звукопровода на процесс распространения волны. Очевидно, что до тех пор пока основная часть мощности расходящейся акустической волны (обычно в пределах главного лепестка диаграммы направленности), проходя весь рабочий участок траектории, не попадет на боковые грани звукопровода, можно считать звукопровод бесконечным в поперечном направлении. В противном случае не­обходимо учитывать наличие отражений от боковых границ, приводящих к появлению в устройстве ложных сигналов. Как правило, последние исключают соответствующими приемами, например выбором поперечных размеров, выпол­нением рифлений или нанесением поглотителей на боковые грани звукопровода. В связи с этим на практике при расчетах обычно можно не учитывать ограни­ченность поперечных размеров звукопроводов.

Ограниченность продольных размеров звукопровода приводит к появлению волн, отраженных от границ. Рассмотрим два типа границ — границу с жест­кой связью, на которой одноименные компоненты вектора смещений и тензора напряжений равны между собой:

(1.19)

и свободную границу, на которой равны нулю нормальные компоненты тензора напряжений:

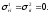(1.20)

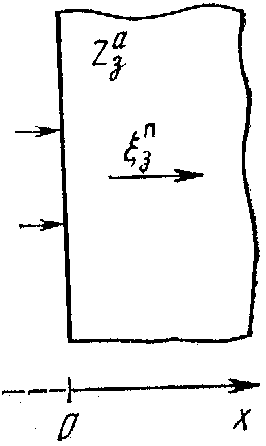
Граница первого типа реализуется при наличии “склейки” (акустической “связ­ки”) между контактирующими телами, а второго — на границе твердого тела с вакуумом (практически с газом при обычных условиях). Другие типы граничных условий сравнительно редко встречаются при анализе акустоэлектронных устройств. Решение задачи об отражении акустических волн от границ деталь­но описано в литературе, мы же кратко приведем результаты для частного случая, который понадобится при расчете преобразователей, а именно для отражения плоской акустической волны, падающей нормально к границе. В связи с тем, что при нормальном падении трансформация типец волн отсутствует и задача является одномерной, в целях упрощения записи будем опускать индексные обозначения оси, а также компонент векторов и тензоров. Кроме этого, условимся о следующем правиле знаков (выборе положи тельных направлений сил давления и колебательных скоростей), которыми и будем везде пользоваться в данной книге: обе величины будем считать положи тельными, если они направлены противоположно направлению внешней нормали к рассматриваемой границе (рис. 1.5).

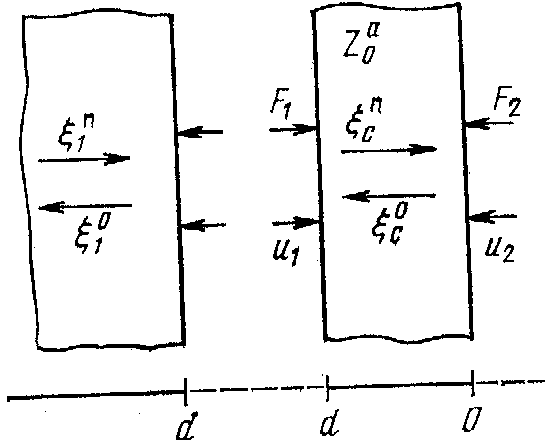
Плоскопараллельный слой вы­дает трансформацию акустического импеданса, в связи с чем его можно использовать в качестве элемента для акустического согласования. Изложенная методика позволяет рассчитать импеданс нескольких граничащих друг с другом плоских слоев последовательным применением, начиная с самой дальней границы по ходу распространения волны. Такая мето­дика расчета проще, чем перемножение матриц, описывающих свойства промежуточных слоев.

Рис.1.5. К расчёту коэффициентов отражения и пропускания плоской границе (а) и плоско-паралельного слоя (б) при нормальном падения акустической волны.

Наряду с объемными волнами, которые могут распространяться в однородном твердом теле, существует особый вид акустических волн, называемых поверхностными, которые распространяются вдоль границы тела, оставаясь локализоваными вблизи этой границы. Поверхностные акустические волны (ПАВ) широко используются в акустоэлектронных устройствах. В настоящее время наиболее изучены три типа ПАВ, которые могут распространяться вблизи плоской поверхности изотропного тела — волны Релея, Лява и Стоунли.

Релеевская волна, как следует из выражения (1.27), обладает “прямолинейным” фронтом, поскольку в любой плоскости, параллельной поверхности, линии постоянной фазы являются прямыми. Используя понятие сагиттальной плоскости — плоскости, перпендикулярной свободной поверхности, вдоль которой распространяется волна, и параллельной ее волновому вектору q (см. рис.1.6) можно сказать, что волна имеет “прямолинейный” фронт, если смещения любой глубине не зависят от расстояния до сагиттальной плоскости. Решение задачи о распространении релеевской волны подробно описано в моногрг, а в варианте изложения — в обзоре, в связи с этим нет необходимости его здесь рассматривать. Обратим лишь внимание, на то что конкретный вид решения зависит от выбора положительного направления оси Оху, а также от принятого при расчете вида экспоненциального множителя, характеризующего распространение волны. К сожалению, в настоящее время выбор направления оси, ни вид экспоненциального множителя не унифицированы, в связи с чем решения, приводимые в работах разных авторов, отличаются по форме. Расчет показывает, что в релеевской волне смещение на любой глубине происходит по эллипсу, плоскость которого лежит в сагитттальной плоскости, а большая ось перпендикулярна свободной поверхности Релеевская волна локализуется вблизи поверхности в слое, толщина которого сравнима с длиной волны.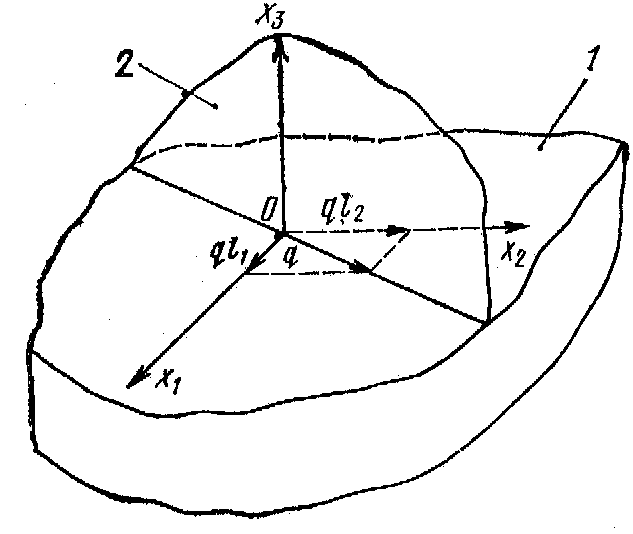

Для релеевской волны так же, как и для объемной, можно ввести нон акустического импсданса, величина которого определяется только физически свойствами полупространства. Однако ввиду того, что структура релеевской волны изменяется с глубиной, аналитическое выражение для акустического импеданса релеевской волны очень громоздко.

Рис. 1.6. Система координат в полупространстве, по поверхности которого распространяется ПАВ.

1-плоская свободная поверхность полупространства; 2-сагиттальная плоскость.

Аналогично объемной волне поверхностная волна с фронтом ограниченная до поперечных размеров испытывает дифракционное расширение.

Вторым основным типом ПАВ является волна Лява, которая может распространяться по границе полубесконечного твердого тела с расположенным на ней слоем толщиной d (рис. 1.2,г), если скорость распространения поперечной волны в слое меньше, чем в полупространстве (обычно такой слой называют Умедляющим). Подробно задача о распространении волны Лява рассмотрена. Дифракционные эффекты для волн Лява обычно не анализируют, так как этот тип волн в основном используется в акустических волноводах, в которых расхождение волны в поперечном направлении исключено. При нормальном падении на плоскую свободную границу волна Лява, как и волна Релея, испытывает отражение с r_F=1.

Третьим типом ПАВ являются волны Стоунли — волны на плоской границе между двумя жестко скрепленными изотропными телами. В отличие от волн Релея и Лява, в которых энергия волны сосредоточена вблизи свободной поверхности тела и вследствие этого оказывается доступной для отбора, преобразования, усиления и других воздействий, в волне Стоунли энергия распространяется вдоль внутренней границы, исключающей возможность непосредственного доступа. По этому свойству волна Стоунли ничем не отличается от рассмотренных раньше объемных волн. В то же время трудности практической реализации границы с однородными свойствами на большой площади и малым рассеянием акустической волны сводят на нет возможные преимущества, связанные с испо­льзованием волн Стоунли, вследствие чего они не находят практического применения в современных акустоэлектронных устройствах и не будут рассматриваться в дальнейшем.