27. Записати основні закони розподілу н.В.В.: а) рівномірний; б) нормальний; в) показниковий. Пояснити зміст букв. Навести приклади н.В.В., розподілених за цими законами.
1.Рівномірний.Величина
Х розподілена рівномірно у проміжку
(a,b),
якщо усі її можливі значення належать
цьому проміжку і щільність її імовірностей
у цьому проміжку постійна, тобто Величина
визначається умовою нормування Р(а<
X<b)
= C(a
- b)
= 1
Імовірність влучення Х в інтервал (х1, х2) дорівнює відношенню довжини цього інтервалу до довжини усього проміжку (a,b). Цей розподіл задовольняють, наприклад, похибки округлення різноманітних розрахунків. С=const 2. Нормальний. Випадкову величину Х називають розподіленою нормально, якщо щільність її імовірностей має вигляд
,
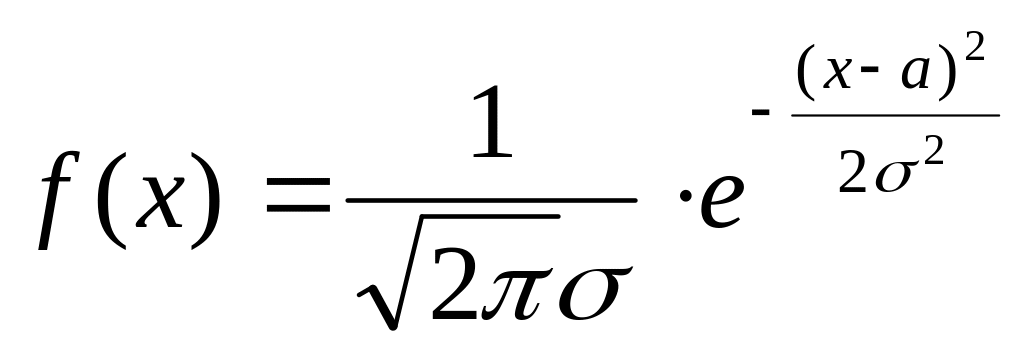де а та σ – параметри розподілу.
3. Показниковий. Випадкову величину Х
називають розподіленою за показниковим
законом, якщо щільність її імовірностей
має вигляд Показниковому розподілу
задовольняють : час телефонної розмови,
чс ремонту техніки, час безвідмовної
роботи комп’ютера. Якщо НВВ Х розподілена
за показниковим законом, то вона має
математичне сподівання та середнє
квадратичне відхилення рівні.
28. Пояснити зміст терміну «закон великих чисел». Довести нерівність Чебишова в усіх формах. Навести приклади її застосування.
Граничні теореми теорії ймовірностей встановлюють відповідність між теоретичними та дослідними характеристиками випадкових величин або випадкових подій при великій кількості випробувань. Граничні теореми описують також граничні закони розподілу. Граничні теореми, які встановлюють відповідність між теоретичними та дослідними характеристиками випадкових подій, об’єднують загальною назвою – закона великих чисел. Нерівність Чебишова. Якщо довільна величина Х приймає тільки невід’ємне значення, то нерівність того, що Х>= не перевищує математичне сподівання. 1 форма нерівності Ч. {x>=1}= M[x] –
Доведення. Припустимо ДВВ має закон розподілу:
Розглянемо
йм. р{x>-1}=
<=
,
a
<=
тобто
. р{x>=1}<=Mx//Нерівність
доведена для Двв
1- р{x>=1}>=1-Mx; р{x<1}>=1-Mx – другий вид 1 форми нерівн. Ч.
Для НВВ
p{x>=1}=
Розглянемо інтеграл
:
<=
<=
Нерівність доведена для НВВ.
2 форма нерівності Ч. якщо довільна ВВ Х має скінчений мат.сподів. і дисперсію, то для будь якого як завгодно малого додатного числа E має місце така нерівність:
p{|X-Mx|>=E}<=D[x]/E^2. Доведення:
Розглянемо подію |X-Mx|>=E→(X-Mx)^2>=E^2→(X-Mx)^2/E^2>=1
P{(X-Mx)^2/E^2>=1}<=M[(X-Mx)^2/E^2]=1/E^2 * M[(X-mx^2)]=1/E^2*Dx Отже
p{|X-Mx|>=E}<=D[x]/E^2.
1- p{|X-Mx|>=E}>=D[x]/E^2; p{|X-Mx|>=E}<=1-D[x]/E^2. – 2 вид 2 форми нерівн Ч.
29 Сформулювати основні теореми закону великих чисел: а) Бернуллі; б) Чебишова; Пояснити значення цих теорем для практики.
а) Теорема Бернуллі: Нехай проводиться n повторних незалежних випробувань, в кожному з яких деяка подія А може настати з йм. Р або не настати з йм. q=1-p.k-число появ події в n випробувань тоді для як завгодно малого E>0 має місце рівність: k/n – відносна частота
p{|k/n-p|<E}→1,
n→∞
Відносна частота збігається до ім.. за йм. Доведення: M[k/n]=1/n*M[x]=1/n*np=p D[k/n]=1/n^2*D[x]=1/n^2*npq=pq/n p{|k/n-p|<E}>=1-pq/nE^2
б) Чебишова: ВВ х назив. попарно незалежні, якщо незалежні є будь які дві з них незалежні
ВВ х:
назив. Взаємнонезалежними, якщо
незалежними в сутності є випадкові
події {Xi<xi},
де хі – довільні дійсні числа. Дисперсія
суми або різниці незалежна або попарно
незалежних ВВ дорівнює суми їх дисперсій:
D[xi+-x2+-…+-xn]=
Нехай xi-довільні попарно незалежні ВВ з скінченими мат. Сподіваннями. Обмеженими дисперсіями (D[xi]<=D), тоді для будь якої як завгодно малого додатного Е має місце рівність: