54 Дати означення вибіркових: а)моди і медіани; б) початкового та центрального моментів; в) коефіцієнтів асиметрії та ексцесу. Навести приклади знаходження (обчислення).

А) Мода для д.в.в – це те значення Хі імовірність якого є найбільшою, при цому якщо всі значення Хі мають однакові імовірності,то будемо вважати,що д.в.в не має моди. Для н.в.в мода – це те значення Хі в якому f(х) набуває найбільшого значення,а я якщо не ма найбільшого значення,то моди для н.в.в не існує. Якщо f(х) є (а;б),то за моду приймають середину цього інтервалу.

Медіана в.в.х наз таке число х=Ме, для якогоF(Ме)больше равно ½, а функція F(Me+0)больше равно 1/2

Б) Початковий емпіричним моментом порядку k називают звичайний момент порядку k при C=0: M_k=(∑n_{i *} x_i^k)/n

Центральним емпіричним моментом порядку K називают звичайний момент порядку k при C=x_в:

m_k=(∑n_i(x_i - x_в)^k)/n

55 Дати означення: а) інтервальної оцінки параметра генеральної сукупності, її точності та надійності; б) надійного інтервалу. Навести приклади.

А) Інтервальну оцінку називають, яка визначається двома числами – кінцями інтервалу. Інтервальні оцінки дозволяють встановити точність і надійність оцінок.

величина δ визначає точність інтервальної оцінки: чим менше δ, тим вища точність.

δ називається граничною помилкою і обчислюється за формулою: δ=t* μ,

де величина t називається довірчим числом (або коефіцієнтом довіри), а μ – середньою (або стандартною) помилкою. Надійність γ – імовірність з якою заданий надійний інтервал накриває параметр генеральної сукупності. Ця надійність знаходиться за формулою , де – інтегральна функція Лапласа. Б) Інтервальною оцінкою (або надійним, або довірчим інтервалом) параметра генеральної сукупності називається такий інтервал , який із заданою надійністю (або надійною, або довірчою імовірністю) γ накриває параметр , що оцінюється. При цьому , , де – точкова оцінка (або вибіркове значення) параметра , величина δ граничною помилкою.

56. Вивести формули для обчислення кінців надійного інтервалу для оцінки математичного сподівання нормального розподіленої генеральної сукупності з: а) відомим; б) невідомим значенням генерального середнього квадратичного відхилення. Навести приклади.

А) Нехай кількість ознак Х генеральної сукупності розподілені нормально, також середнє квадратичне відхилення відоме σ , спробуємо оцінити невідоме мат.сподівання =а за вибірковою середньою . Поставимо своєю задачею знайти довірчі інтервали, які накривають параметр а з надійністю . Будемо розглядати вибіркову середню як випадкову величину і вибіркові значення ознаки х1,х2,….хn – як однаково розподілені незалежні випадкові велечини Х1,Х2…..,Хn. Іншими словами математичне сподівання кожної з цих величин =а и середнє квадратичне відхилення – і .

Параметри розподілу такі: М( )=а, σ( )=

Потрібно щоб виконувалась співвідношеня: Р=( )= - заданна імовірність

Р=( )=2Ф( ) , замінивши Х на і σ на σ( )= , отримаємо Р=( )=2Ф( / )=2Ф(t), де t= / .

57 а)Сформулювати і обгрунтувати взаємозалежність між точністю інтервальної оцінки, її надійністю та обсягом вибірки.б) Вивести формулу для обчислення мінімально необхідного обсягу вибірки для забезпечення заданої точності інтервальної оцінки з заданою надійністю. Навести приклади.

А)Існує певна взаємозалежність між обсягом вибірки п та точністю δ і надійністю γ інтервальної оцінки будь-якого параметра генеральної сукупності незалежно від схеми відбору. Проаналізуємо цю залежність на прикладі інтервального оцінювання генеральної середньої для повторної вибірки: 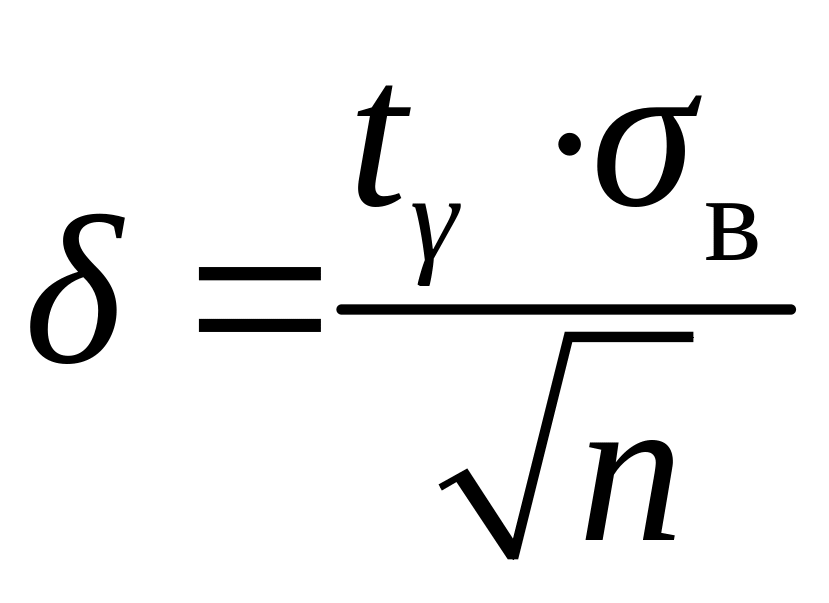Оскільки інтегральна функція Лапласа Ф(х) є зростаючою, то із рівності витікає, що із збільшенням надійності γ збільшується значення довірчого числа t_γ. Це, в свою чергу, призводить до збільшення граничної помилки δ (див. (2.7), тобто зменшення точності оцінки при фіксованому п. Навпаки, збільшення точності оцінки (тобто зменшення δ) неминуче тягне за собою зменшення її надійності γ.

Існує єдина можливість збільшувати надійність без зменшення точності, або збільшувати точність без зменшення надійності, або одночас­но збільшувати точність і надійність – це збільшення обсягу вибірки п.