Связь между прямоугольными и полярными координатами.

П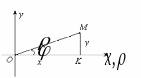 усть полюс системы координат совпадает с началом декартовой системы координат, а полярная ось совпадает с положительной полуосью OX. Тогда из _ΔОМК : - это формулы перехода к декартовой системе координат.

Выведем формулы обратного перехода от декартовых координат к полярным.

Полярный радиус – вектор ρ, будучи расстоянием от точки М до начала координат, будет равен

, а также, , .

Угол определяется из условия: tg = и знаков функций .

Пример.

Найти полярные координаты точки А(3;-4).

= , , , tg = . Так как угол  находится в V четверти, то = - arctg . Отсюда, A(5, - arctg ), или А(5;-53 ⁰).

Полярные уравнения кривых второго порядка.

Кривая второго порядка – это множество точек плоскости, для каждой их которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы) есть величина постоянная, равная эксцентриситету (е).

П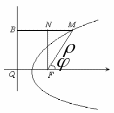 усть F – фокус кривой, BQ отвечающая этому фокусу директриса, FQ =p, пусть полюс полярной системы координат совпадает с F, а полярная ось перпендикулярна BQ и направлена как указано на рисунке.

Пусть M – любая точка кривой. Тогда, согласно определению кривой, . Так как , , то , откуда .

При этом: - окружность; 0< e <1 – эллипс; e = 1 – парабола; e >1 – гипербола.

Примеры на тему: ”Кривые второго порядка”.

Пример 1. Установить, что уравнение 5x²+9y²-30x+18y+9=0 определяет эллипс. Найти его центр С, полуоси, координаты фокусов F₁, F₂, эксцентриситет и уравнения директрис. Сделать чертеж.

Решение: 1. В заданном уравнении сгруппируем слагаемые, содержащие одноименные координаты и вынесем коэффициенты при квадратах за скобки:

5(x²-6x)+9(y²+2y)+9=0.

Дополним выражения, стоящие в скобках, до полного квадрата и полученные свободные константы перенесем в правую часть:

5(x²-6x+9-9)+9(y²+2y+1-1)+9=0,

5((x-3)²-9)+9((y+1)²-1)+9=0,

5(x-3)²+9(y+1)²=45.

Разделим обе части уравнения на 45, получим

.

2. Введем новую систему координат XOY, полученную сдвигом по каждой из координатных осей, и связанную со старой декартовой системой координат равенствами:

(1).

Тогда, исследуемое уравнение кривой относительно новых осей примет вид:

, .

Это есть канонический вид эллипса с центром (0,0), большой полуосью a=3, малой полуосью b= . Фокусы эллипса располагаются на оси OX на расстоянии с= от начала координат О, в точках ₁(с, 0), ₂(-c, 0) в новой системе координат XOY.

Вычисляем, с= = =2, ₁(2, 0), ₂(-2, 0). Мера сжатия, то есть эксцентриситет, дается равенством = . Отсюда = .Директрисы эллипса в системе XOY задаются уравнениями X= . В нашем случае, X= .

3. Чтобы найти координаты центра и фокусов в старой системе xoy, воспользуемся равенствами (1), осуществляющими связь систем координат:

центр С: , C(3, -1),

фокусы F₁ : _, F₁(5,-1), F₂: , F₂(1,-1).

Уравнения директрис: x-3= .

4. Теперь построим эллипс. С помощью параллельного переноса системы координат xoy образуем новую систему

к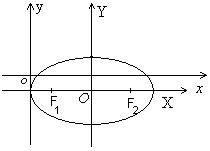 оординат XOY так, чтобы новое начало координат О совпадало с точкой С(3, -1). При указанном выборе, оси координат системы XOY являются осями симметрии эллипса, а точка О- центром симметрии. Теперь симметрично О по оси OX отложим отрезки длины a=3, а по оси OY отрезки длины .

Соединив найденные вершины, получим эллипс. На оси OX симметрично относительно О на расстоянии с=2 отложим точки F₁, F₂-фокусы эллипса. Так как директрисы эллипса описываются уравнениями x=const, то они располагаются параллельно OY, причем одна из них проходит через

точку (7,5 ; 0), другая через (-1,5; 0).

Пример 2. Установить, что уравнение 16x²-9y²-64x-54y-161=0 определяет гиперболу. Найти ее центр С, полуоси, координаты фокусов F₁, F₂, вершины А_1, А₂ , эксцентриситет , уравнения директрис и асимптот. Сделать чертеж.

Решение: 1. В уравнении линии выделим полные квадраты при одноименных переменных:

16(x-2)²-9(y+3)²=144.

Разделив обе части уравнения на 144, будем иметь:

.

2. Введем новую систему координат XOY, полученную сдвигом по каждой из координатных осей и связанную с xoy равенствами:

(2).

В этой системе исследуемое уравнение представляет собой каноническое уравнение гиперболы:

с центром в точке O (0,0), вещественной полуосью а=4 и мнимой b=4. Точки ₁(с, 0), ₂(-c, 0), где с= являются фокусами гиперболы, отсюда находим с= =5, ₁(5, 0), ₂(-5, 0). Эксцентриситет = , в нашем случае = . Вершины гиперболы располагаются по оси OX симметрично относительно начала координат и на расстоянии a=3 от центра, поэтому ₁(3, 0), ₂(-3, 0). По формулам асимптот и директрис:

Y= X и X= , найдем

Y= X - уравнения асимптот, X= -уравнения директрис.

3. Вернемся к исходной системе координат xoy, воспользовавшись равенствами (2):

C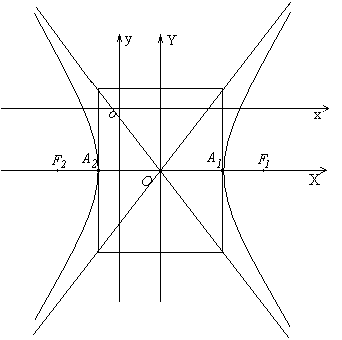 (2;-3), F₁(7;-3), F₂(-3; -3), A₁(5; -3), A₂(-1; -3), асимптоты: y+3= (x-2), директрисы: x-2= .

4. Теперь построим гиперболу. С помощью параллельного переноса системы координат xoy образуем новую систему координат XOY так, чтобы новое начало координат О совпадало с точкой С(2, -3). При указанном выборе, оси координат системы XOY являются осями симметрии гиперболы, а точка О- центром симметрии.

Теперь симметрично О по оси OX отложим отрезки длины a=3, а по оси OY отрезки длины b=4, образуем основной прямоугольник гиперболы. При пересечении основного прямоугольника с осью OX образуются вершины А₁, А₂. Через противоположные вершины основного прямоугольника проведем прямые, которые будут являться асимптотами гиперболы. Теперь проводя через вершины и приближаясь к асимптотам,

рисуем ветви гиперболы. F₁, F₂-фокусы гиперболы располагаются по оси абсцисс OX симметрично начала координат О на расстоянии с=5.

Пример 3. Установить, что уравнение x=-2y²+12y-14 определяет параболу, найти ее вершину, параметр, фокус, директрису. Сделать чертеж.

Решение: 1. В заданном уравнении сгруппируем слагаемые содержащие переменную y, вынесем коэффициент при квадрате за скобку и выделим полный квадрат:

x= -2(y-3)²+4, x – 4= -2(y-3)².

2. Введем новую систему координат XOY, связанную со старой , следующими формулами:

, (3)

тогда исследуемое уравнение относительно новых осей примет вид:

X= -2Y² , Y²= - X.

Полученное уравнение представляет собой каноническую форму уравнения параболы, симметричной относительно оси OX, с ветвями, направленными в отрицательную сторону OX, и вершиной в точке (0; 0). Константа перед X, есть величина 2p, поэтому 2p= , а параметр p= . Фокус и уравнение директрисы при таком расположении параболы находятся по формулам , X= , отсюда имеем фокус , директриса X= .

3. Вернемся к исходной системе координат xoy. Используя равенства (3), получаем: A(4;3), F(3 ; 3), директриса x=4 .

4 . Построение параболы. С помощью параллельного переноса системы координат xoy так, чтобы новое начало координат О совпадало с точкой А(4; 3), образуем новую систему XOY.

Рисуем параболу с вершиной в точке А=О и обладающую перечисленными выше свойствами.

Фокус параболы лежит на расстоянии = от вершины. Директриса параболы проходит через точку (4 ; 0) параллельно OY.