
- •Н.П. Шевченко, и.Ю. Смирнова аналитическая геометрия и линейная алгебра
- •Аналитическая геометрия.
- •Лекция 1. Линейные образы в r2. Понятие об уравнении линии на плоскости.
- •Прямая линяя на плоскости.
- •Типы уравнений прямой.
- •Угол между двумя прямыми. Условие параллельности и перпендикулярности.
- •Задачи на тему “Прямая на плоскости”.
- •Лекция 2. Линейные образы в r3 .
- •Понятие алгебраической поверхности.
- •Плоскость.
- •Прямая линяя в пространстве.
- •Канонические уравнения прямой в пространстве.
- •Приведение общих уравнений прямой к каноническому виду.
- •Угол между двумя прямыми.
- •Задачи на тему “Прямая в пространстве”.
- •Прямая и плоскость.
- •Условие того, что прямая лежит в данной плоскости.
- •Условие того, что две прямые лежат в одной плоскости.
- •Смешанные задачи на прямую и плоскость.
- •Лекция 3. Кривые второго порядка.
- •1. Окружность
- •3. Гипербола
- •4. Парабола
- •Преобразования координат.
- •Кривые 2-го порядка с осями симметрии, параллельными осям координат.
- •1.Эллипс.
- •2.Гипербала.
- •3. Парабола.
- •Полярная система координат.
- •Связь между прямоугольными и полярными координатами.
- •Полярные уравнения кривых второго порядка.
- •Примеры на тему: ”Кривые второго порядка”.
- •Лекция 4. Поверхности второго порядка.
- •Лекция 5. Линейная алгебра. Матрицы.
- •Линейные операции над матрицами.
- •1. Сложение матриц.
- •2. Умножение матрицы на число.
- •3. Транспонирование матриц.
- •4. Умножение матриц.
- •5. Обратная матрица.
- •Свойства столбцов матрицы а.
- •Базисный минор.
- •Элементарные преобразования матриц.
- •Задачи на тему “Матрицы”.
- •Лекция 6. Системы линейных алгебраических уравнений. Однородные системы линейных уравнений.
- •Методы решения системы линейных алгебраических уравнений.
- •1. Правило Крамера.
- •Решение системы методом обратной матрицы.
- •3. Метод Гаусса.
- •Множество решений однородной системы.
- •Общая теория линейных систем.
- •Теорема Кронекера-Капелли.
- •Общее решение системы линейных уравнений.
- •Теорема. Если – фундаментальная система решений системы (7), а - некоторое частное решение системы (6), то общее решение системы линейных алгебраических неоднородных уравнений (6):
- •Задачи на тему “Системы линейных алгебраических уравнений”.
- •Неоднородные системы линейных алгебраических уравнений (слау).
- •Лекция 7. Понятие линейного преобразования. Собственные векторы.
- •Симметрическое линейное преобразование.
- •Теорема. Собственные значения симметрического линейного преобразования вещественны, а собственные векторы ортогональны.
- •Преобразование координат при переходе к новому базису (изменение направления осей).
- •Ортогональная матрица.
- •Квадратичные формы. Приведение к каноническому виду.
- •Приведение общего уравнения линии 2-го порядка к каноническому виду.
- •Задачи на темы ”Собственные векторы ”, “Приведение кривой к каноническому виду”.
- •Лекция 8. Линейные пространства.
- •Примеры векторных (линейных) пространств.
- •Пример 2. Пространство всех вещественных чисел.
- •Замечание 1. Арифметическое пространство Rn является векторным пространством (удовлетворяет аксиомам 1) – 8)).
- •Замечание .Скалярное произведение порождает норму по правилу .
- •Замечание. Пара (е, (, .)) называется n-мерным Евклидовым пространством; пара (е,ф) со свойствами 1)-3) называется n-мерным аффинным пространством.
- •Используемая литература
- •Оглавление
Прямая линяя в пространстве.
Линия в пространстве определяется как пересечение двух поверхностей, то есть задается совокупностью двух уравнений:
![]()
 .
.
Н
![]()
![]() -
окружность в плоскости z=
-
окружность в плоскости z=
Прямую линию в пространстве можно представить как пересечение двух плоскостей, то есть совокупность двух уравнений плоскостей. Систему двух непараллельных уравнений называют общими уравнениями прямой:
![]() .
.
Канонические уравнения прямой в пространстве.
Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором данной прямой и обозначается: {m,n,p}.
Если известна точка М0(x0, y0, z0), прямой и направляющий вектор {m,n,p}, то прямая может быть определена (двумя) уравнениями вида:
![]() ,
(1)
,
(1)
которые называются каноническими уравнениями прямой.
Канонические уравнения прямой, проходящей через две данные точки М0(x0, y0, z0), M1 (x 1 ,y1, z1) имеют вид:
![]() .
(2)
.
(2)
Обозначив буквой t каждое из равных отношений в канонических уравнениях, мы получим
=
t, отсюда
![]() .
(3)
.
(3)
Уравнения (3) есть параметрические уравнения прямой, проходящей через точку М0(x0,y0, z0), параллельно вектору {m,n,p}. В уравнениях (3) t рассматривается как произвольно изменяющийся параметр; x, y, z - как функции от t. При изменении t величины x, y, z меняются так, что точка М(x,y,z) движется по данной прямой.
Приведение общих уравнений прямой к каноническому виду.
Пусть прямая задана общими уравнениями:
, (1)
где 1{A 1,B1,C1}, 2{A2, B2, C2} – нормальные векторы заданных плоскостей .
Выберем на прямой определенную точку М0(x0, y0, z0). Для этого, например, z0 зададим произвольно, а x0 и y0 получим из системы (1).
В
качестве направляющего вектора возьмем
вектор
![]() :
:
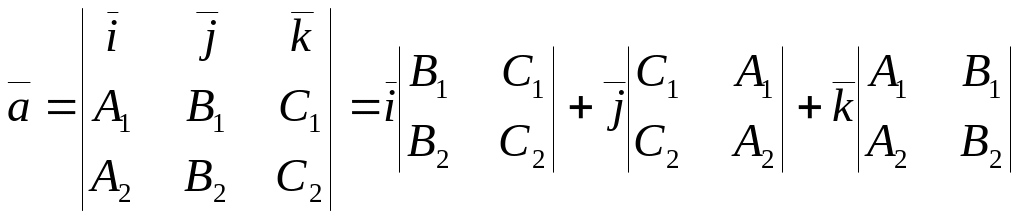 .
.
Следовательно, канонические уравнения прямой, соответствующие системе (1), имеют вид:
 .
.
Угол между двумя прямыми.
За угол между двумя прямыми
![]() ,
,
![]() ,
,
принимается угол между их направляющими векторами.
Здесь
![]() ={m1,n1,p1},
={m1,n1,p1},
![]() {m2,n2,p2}
– направляющие вектора данных прямых,
cos=
{m2,n2,p2}
– направляющие вектора данных прямых,
cos=![]() .
Условие параллельности двух прямых:
.
Условие параллельности двух прямых:
![]() .
.
Условие перпендикулярности двух прямых: m1m2 + n1n2 + p1p2=0.
Задачи на тему “Прямая в пространстве”.
Составить каноническое уравнение прямой L, проходящей через две заданные точки А(1 –2 1), В(3 1 -1).
На прямой L возьмем произвольным образом точку М(x y z) и соединим ее с какой-либо известной точкой на этой прямой, например, точкой А. Образуем текущий вектор
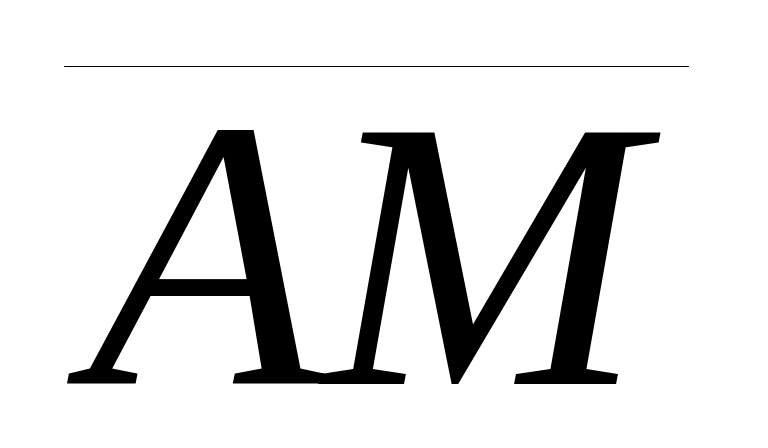 {x-1
y+2 z-1}. Вектор
{x-1
y+2 z-1}. Вектор
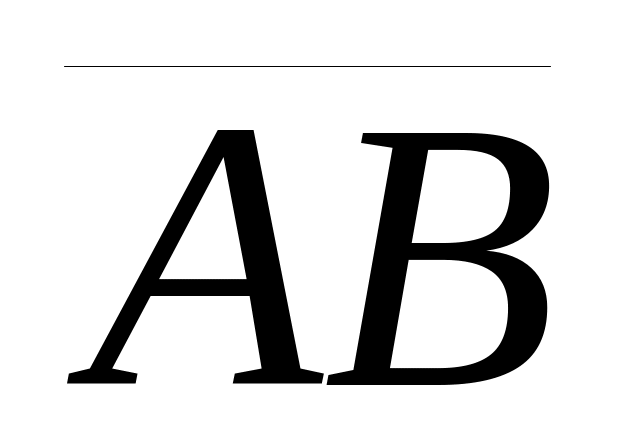 {2
3 -2}, лежащий на прямой L,
является направляющим вектором для L.
Для любой точки М(x y
z)
{2
3 -2}, лежащий на прямой L,
является направляющим вектором для L.
Для любой точки М(x y
z)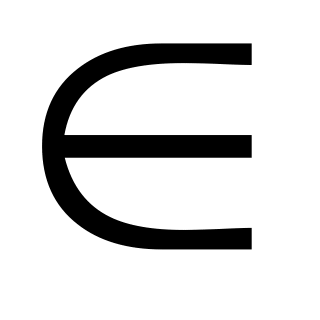 L
вектора
II
,
следовательно, условие параллельности
векторов описывает уравнение прямой
L:
L
вектора
II
,
следовательно, условие параллельности
векторов описывает уравнение прямой
L:
![]() .
.
Составить уравнение прямой
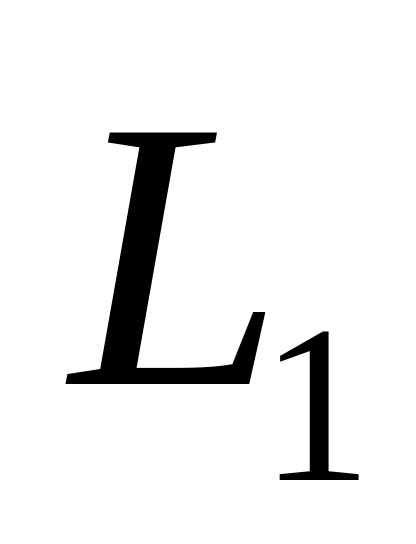 ,
проходящей через точку А(1 –1 2), параллельно
прямой
,
проходящей через точку А(1 –1 2), параллельно
прямой
 :
:
![]()
На
прямой
образуем текущий вектор
{x-1
y+1 z-2}. Из
канонического уравнения прямой
находим направляющий вектор![]() {5
–2 0}, здесь m=5, n=-2,
p=0. Так как
II
,
то
II
для любой точки М(x y
z)
.
Используя теперь условие параллельности,
получаем канонические уравнения прямой
:
{5
–2 0}, здесь m=5, n=-2,
p=0. Так как
II
,
то
II
для любой точки М(x y
z)
.
Используя теперь условие параллельности,
получаем канонические уравнения прямой
:
![]() .
.
Известны уравнения двух прямых:
:
![]() ,
:
,
:![]()
Проверить, являются ли и параллельными.
Проверить, являются ли и перпендикулярными.
Найти угол
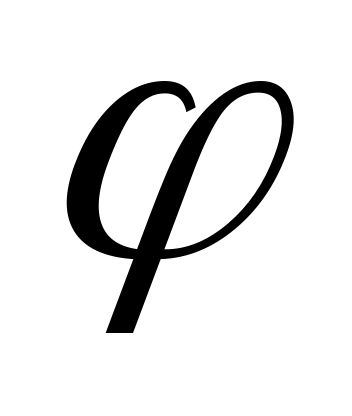 между
и
.
между
и
.
а)
Из условия параллельности прямых имеем,
II
,
если их направляющие вектора
![]() и
параллельны. Координаты вектора
легко получаются из заданных канонических
уравнений прямой
:
{-1
3 1}. Для прямой
,
определяемой пересечением плоскостей,
направляющий вектор
находится как векторное произведение:
=
и
параллельны. Координаты вектора
легко получаются из заданных канонических
уравнений прямой
:
{-1
3 1}. Для прямой
,
определяемой пересечением плоскостей,
направляющий вектор
находится как векторное произведение:
=![]() ,
где
,
где
![]() {1
–1 0},
{1
–1 0},
![]() {2
1 -5}. Вычисляем,
{2
1 -5}. Вычисляем,
=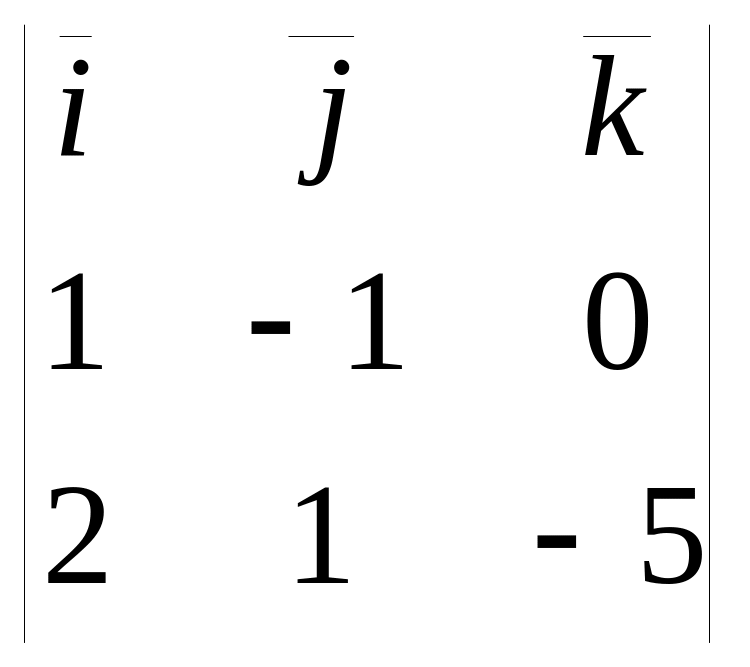 =5
+5
+3
=5
+5
+3![]() ,
{5
5 3}.
,
{5
5 3}.
Так как координаты векторов и не пропорциональны, то условие параллельности для векторов и не выполняется, а значит, не параллельна .
b)
Из условия перпендикулярности прямых,
,
если
.
Так как
![]() =13,
то условие перпендикулярности векторов
и
не выполняется. Стало быть,
не перпендикулярна к
.
=13,
то условие перпендикулярности векторов
и
не выполняется. Стало быть,
не перпендикулярна к
.
c) Угол между прямыми найдем по формуле:
cos
=соs(
,
)=![]() .
.
Отсюда,
соs
=![]() .
.
Привести к каноническому виду уравнения прямой:
![]() .
.
Найдем
направляющий вектор прямой
![]() :
:
=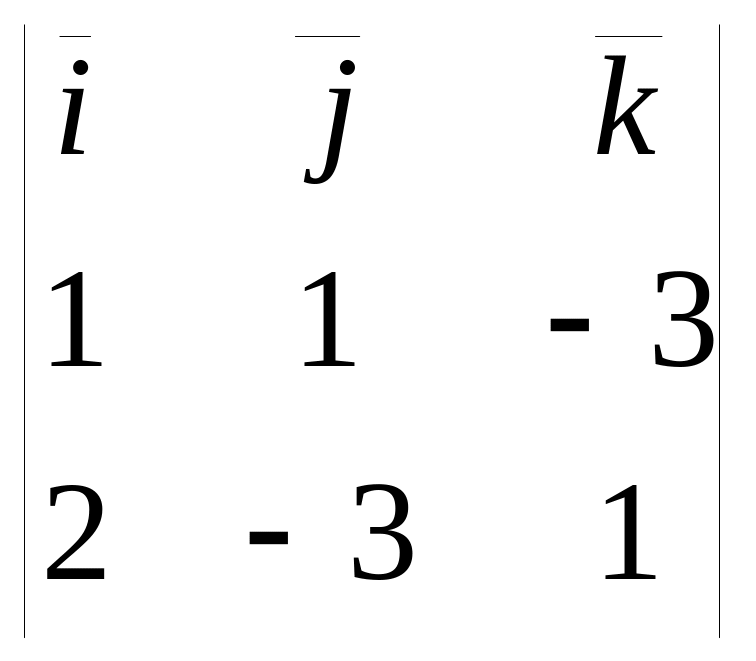 =-8
-7
-5
,
{-8
–7 -5}.
=-8
-7
-5
,
{-8
–7 -5}.
За точку М0(x0 y0 zo), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью YOZ. Так как при этом x0=0, то координаты y0,z0 определяются из заданного уравнения прямой, если в нем положить x=0:
![]() .
.
Откуда
находим z0=![]() ,
y0=
,
y0=![]() и M0(0
).
и M0(0
).
Итак, воспользовавшись теперь общей формулой канонических уравнений прямой, получаем:
 .
.
