2. Тест Глейзера:

Тест Глейзера относится к тестам гетероскедастичности и основывается на регрессии абсолютных значений остатков, то есть рассматривается функция |e_i| = a + b*x^c + u. c – какое-либо число, например, c = – 1; – 0,5; 0,5; 1. Регрессия абсолютного значения остатка от фактора х строится при разных значениях параметра с; далее отбирается та функция, для которой коэффициент регрессии b оказывается наиболее значимым, то есть имеет место наибольшее значение критерия Стьюдента или критерия Фишера и детерминации.

3. Тест Уайта:

Тест предполагает, что дисперсия ошибок регрессии представляет собой квадратичную функцию от значений факторов, то есть:

e² = a + bx + cx² + u

e² = a + b₁x₁ + b₁x₁² + b₂x₂ + b₂x₂² + u.

Так что модель включает не только значения факторов, но и их квадраты, а также попарные произведения. Поскольку каждый параметр модели e² = f (x) должен быть рассчитан на основе достаточного числа степеней свободы, то чем меньше объем совокупности, тем в меньшей мере квадратичная функция сможет содержать попарные произведения факторов.

31. Применение обобщенного метода наименьших квадратов (ОМНК) для случая гетероскедастичности остатков

Невозможность или нецелесообразность использования традиционного МНК по причине проявляющейся в той или иной степени гетероскедастичности привели к разработке обобщенного метода наименьших квадратов (ОМНК). Фактически при этом корректируется модель, изменяются ее спецификации, преобразуются исходные данные для обеспечения несмещенности, эффективности и состоятельности оценок коэффициентов регрессии.

При нарушении гомоскедастичности и наличии автокорреляции (это статистическая корреляция между случайно распределенными в пространстве переменными одного и того же типа, атрибута, имени и т.д., когда корреляция зависит от расстояния и/или направления между местоположениями) рекомендуют заменять МНК на ОМНК.

Отличие: применяется к преобразованным данным и не только получает несмещенные оценки, но и оценки эти имеют меньшие выборочные дисперсии.

Предполагаем:

-среднее остатков равно нулю,

-гипотеза: их дисперсия уже не является постоянной, она пропорциональна x²

-сама величина дисперсии, входящая общим множителем при этих коэффициентах пропорциональности, неизвестна.

-исходная модель после введения этих коэффициентов в уравнение множественной регрессии продолжает оставаться гетероскедастичной:

y = a + bx + e *корень из(x)

-пусть эти остаточные величины (остатки) не являются автокоррелированными.

1. Введем новые переменные, получающиеся делением исходных переменных модели, зафиксированных в результате i-наблюдения, на корень квадратный из коэффициентов пропорциональности Кi:

y / к.из(x) = (a / к.из(x)) + (bx / к.из(x)) + e

y / к.из(x) = Y

1 / к.из(x) = Z

2. Получим новое уравнение в преобразованных переменных, в котором уже остатки будут гомоскедастичны. Сами новые переменные — это взвешенные исходные переменные:

Y = aZ + b* к. из(x) + e

3. Необходимо минимизировать величину отклонений У; получим систему нормальных уравнений:

Σ (YZ) = a*Σ Z² + b*Σ (z * к.из(x))

Σ Y к.из(x) = a*Σ (Z *к.из(x)) + b*Σ x

4. Определяем коэфф. регрессии b в ОМНК, как взвешенную величину по отношению к обычному МНК с весами 1 / к.из(x). Преобразовываем систему:

Σ (y/x) = a*Σ (1/x) + n*b

Σ y = n*a + b*Σ x

или

y / к.из(x) = a’ / к.из(x) + b’*x / к.из(x) + e

y = a’ + b’*x.

Вывод: Если в модели обнаружена гетероскедастичность, то ее можно устранить с помощью ОМНК. Все зависит от того, насколько точно мы можем оценить дисперсию ошибок наблюдений. Если мы нашли переменные, которые хорошо их описывают, то ОМНК будет работать.

Недостатки (две технические проблемы)

1. в преобразованной регрессии не будет константы, поэтому коэффициент детерминации перестает быть хорошим измерителем качества регрессии.

2. мы делим все переменные в уравнении регрессии на одну и ту же переменную, это может привести к возникновению ложных связей и мультиколлинеарности (тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат).

КРАТКО:

1. Преобразование исходных переменных:

_t’ = y_t – r_b * y_t-1

x_t’ = x_t – r_b * x_t-1

2. Применение обычного МНК к уравнению и определение a* и b:

y_t’ = a’ + b*x_t’ + V_t

3. Расчет параметра a:

a = a’ / (1 - r_b)

4. Переход к исходному уравнению:

y_t = a + b*x_t + e_t

32. Мультиколлинеарность факторов – понятие, проявление и меры устранения

Проблемы, возникающие при построении регрессионных моделей:

1. Гетероскедастичность.

2. Мультиколлинеарность.

Мультиколлинеарность — тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат.

Симптомы М.:

1. завышенное значение коэффициента детерминации r²;

2. высокие стандартные ошибки для коэффициентов регрессии b;

3. широкие доверительные интервалы (для b);

4. низкое значение t-критерия;

5. появление при коэффициентах регрессии b знаков, противоположных ожидаемым.

Методы по устранению М.:

1. Удаление из модели переменных с высоким коэффициентом парной корреляции r между факторами, если это не противоречит теории, положенной в основу построения модели.

2. Увеличение числа наблюдений n.

3. Изменение функциональной формы модели.

4. Использование априорной информации.

5. Построение моделей по отклонениям от средней величины.

6. Использование специальных методов обработки временных рядов.

33. Специфика временного ряда как источника данных в эконометрическом моделировании

Временной (динамический) ряд – это ряд последовательно расположенных во времени числовых значений соответствующего показателя

Элементы временного ряда:

1. уровни ряда (y_t)- числовые значения того или иного показателя;

2. время (t).

Виды временных рядов:

1. моментные, если время задано моментами;

2. интервальные, если время задано интервалами.

Модели на основе рядов динамики:

1. Модели изолированного динамического ряда.

2. Модели системы взаимосвязанных рядов динамики.

3. Модели авторегрессии.

4. Модели с распределенным лагом.

Компоненты временного ряда:

1. Тенденция (T) – характеризует воздействие всех факторов на динамику изучаемого показателя.

2. Периодические колебания (P)

3. Случайные колебания (E)

y_t = f (T, P, E)

Графики:

1. Ряд без тенденции и периодических колебаний: y_t = y + E;

2. Ряд с тенденцией: y_t = f (T) + E;

3. Ряд с периодическими и случайными колебаниями y_t = f (P, E);

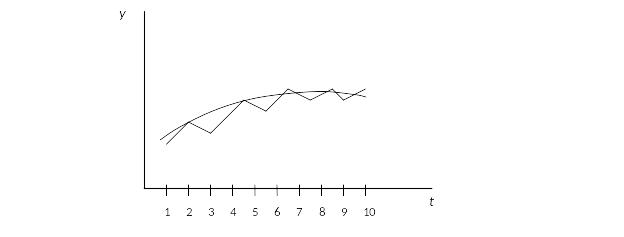
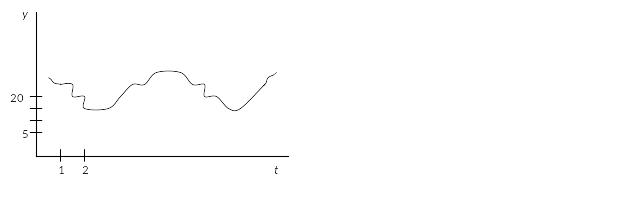
4 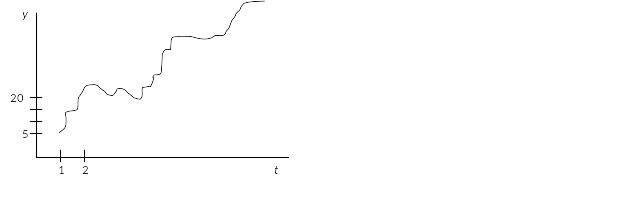. Ряд с тенденцией, периодическими и случайными колебаниями y_t = f (T, P, E).

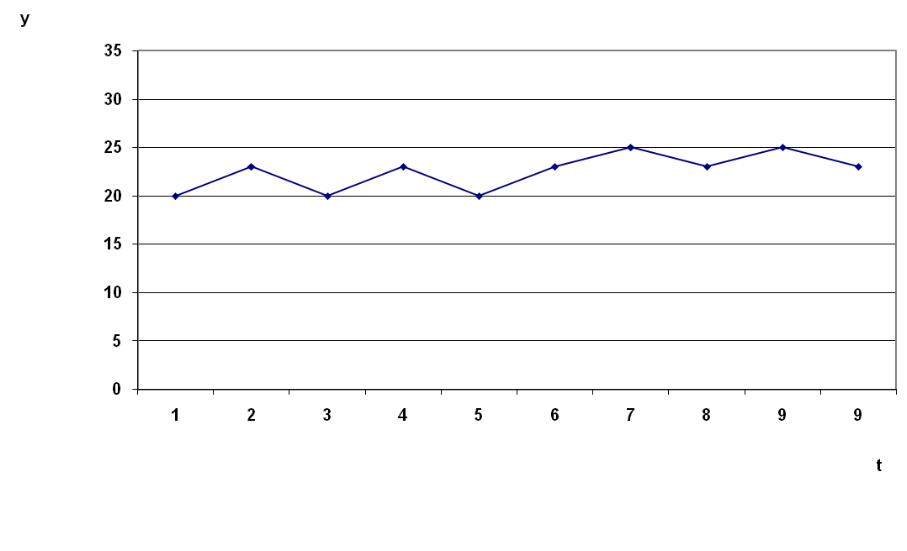
34. Автокорреляция уровней временного ряда и ее последствия

Автокорреляция уровней временного ряда - корреляционная зависимость между последовательными значениями уровней временного.

r_ytyt-1 = (y_ty_t-1cp – y_{t cp} * y_t-1cp) / δ_ytδ_yt-1

r_ytyt-1 = (Σ(y_t – y_{t cp})* (y_t-1 - y_t-1cp)) / к.из(Σ(y_t – y_{t cp})²*(y_t-1 - y_t-1cp) ²)

Последствия:

1. Оценки параметров, оставаясь линейными не смещенными, перестают быть эффективными, они перестают обладать свойствам наилучших линейных несмещенных оценок

2. Дисперсии оценок являются смещенными.

3. Зачастую дисперсии являются заниженными, что привод к увеличению t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые могут ими и не являться.

4. Коэф. регрессии и детерминации м.б. не верными, следовательно ухудшаются прогнозные качества модели.

35. Моделирование тенденции временных рядов

Метод аналитического выравнивания сводится к замене фактических данных сглаженными, определенными по выбранной математической функции. При этом, уровни временного ряда рассматриваются как функция от времени: y_t = f(t)

Этапы построения модели тенденции (уравнения тренда):

1. Выбор математической функции, описывающей тенденцию;

2. Оценка параметров модели;

3. Проверка адекватности выбранной функции и оценка точности модели;

4. Расчет точечного и интервального прогнозов;

Виды математических функций, описывающих тенденцию:

1. Функции с монотонным характером возрастания (убывания) и отсутствием пределов роста (сниж-я);

2. Кривые с насыщением, т. е. устанавливается нижняя или верхняя граница изменения уровней ряда;

3. S-образные кривые, т. е. кривые с насыщением, имеющие точку перегиба.

36. Оценивание параметров в уравнениях тренда

Уравнения трендов:

1. Линейная y = a + bt

2. Гипербола y = a + b/t

3. Парабола второго порядка y = a + bt + ct²

4. Степенная функция y = at^b

5. Показательная функция y = ab^t

6. Экспонента y = e^{a + bt}

7. Обратная модель y = 1/(a + bx)

8. Логарифмическая y = a + b*lnx

Эконометрическое оценивание моделей включает два основных этапа:

1. Теоретический. Считается, что определена генеральная совокупность. Зная ее статистические свойства, м. теоретически определить параметры модели.

2. Эмпирический. Используются выборочные данные. Можно оценить, но нельзя точно определить значения параметров модели, т.к. они являются случайными величинами.

Параметры - характеристики генеральной совокупности. Оценки - характеристики выборочной совокупности.

Оценка генеральных параметров может быть получена двумя методами:

а) МНК – используется чаще;

б) методом максимального правдоподобия.

Требования к оценкам (свойства):

1. Несмещенность. В среднем оценка соответствует параметру при любом объеме выборки.

2. Эффективность. Несмещенная оценка эффективна, если она имеет мин. дисперсию по сравнению с другими выборочными оценками. Та из оценок, которая имеет меньшую дисперсию, является более эффективной.

3. Состоятельность. Оценка состоятельна, если при увеличении объема выборки она стремится к оцениваемому параметру. Т.е. х_ср не отличается от µ, когда n → ∞.

Рассмотрим линейный тренд:

t	y = a + bt	∆y = yt – yt-1
1	a + b	-
2	a + 2b	b
3	a + 3b	b
4	a + 4b	b

Можно вывести формулы для нахождения параметров системы:

b = ((y_t*t)_ср - y_{t ср} * t_ср) / (t²_ср – t_ср²); а = y_{t cp} - b*t_ср.

а - свободный член уравнения регрессии; экономически не интерпретируется.

b - абсолютный показатель силы связи (в лин. ур-ии). Наклон линии регрессии или коэффициент регрессии. Мера зависимости у от х.

Σt = 0; a = Σy / n; b = Σyt / Σt²

Система норм. ур-ий: Σy = na + bΣt

Σyt = aΣt + bΣt²

37. Модели сезонности: аддитивная и мультипликативная

Метод аналитического выравнивания сводится к замене фактических данных сглаженными, определенными по выбранной математической функции. При этом, уровни временного ряда рассматриваются как функция от времени: y_t = f(t).

Учет сезонности при построении модели регрессии y = a +bx_t + c₁z₁ + c₂z₂ + c₃z₃:

z1 = 1 – для первого квартала, z1 = 0 – для остальных;

z2 = 1 – для второго квартала, z2 = 0 – для остальных;

z3 = 1 – для третьего квартала, z3 = 0 – для остальных.

Тимы моделей:

1. Аддитивная модель - модель, в которую факторы входят в виде алгебраической суммы; приблизительно равная сезонная вариация указывает на существование аддитивной модели: y_t = T+S+E

2. Мультипликативная модель - модель, в которую факторы входят в виде произведения; усиление сезонной вариации с возрастанием тренда указывает на существование мультипликативной модели: y_t = T*S*E

Построение аддитивной модели:

1. Нахождение сглаж. уравнений динамич. ряда методом скользящих средних

2. Оценка сезонной компоненты и ее корректировка

3. Элиминирование сезонной компоненты из исходных данных временного ряда

4. Построение уравнения линейного тренда по уровням ряда с элиминированием сезонности

5. расчет выровненных значений трендовой составляющей

6. расчет теоретических уровней ряда с учетом сезонности

7. расчет случайной компоненты, позволяющей оценить качество построенной модели .

Аддитивная. Мультипликативная

38. Исключение тенденции на основе метода отклонений от тренда

Тенденция (T) – характеризует воздействие всех факторов на динамику изучаемого показателя.

Существует 3 метода исключения тенденции:

- Метод отклонений от тренда;

- Метод последовательных разностей;

- Включение в модель регрессии по временным рядам фактора времени.

1. e_yt = y_t – y_{t с крыш} ; e_xt = x_t – x_{t с крыш}

e_yt = a – b*e_xt

2. (y_t – y_{t с крыш}) = a + b*(x_t - x_{t с крыш})

y_t = y_{t с крыш} + a + b*(x_t - x_{t с крыш})

y_p = y_{t=p с крыш} + a + b*(x_p – x_{t=p с крыш})

y_p - прогнозное значение у;

y_{t=p с крыш} - прогноз у по тренду при t=p;

x_p - прогнозное значение х;

x_{t=p с крыш} - прогноз х исходя из уравнения тренда при t=p.

39. Исключение тенденции на основе метода последовательных разностей

Тенденция (T) – характеризует воздействие всех факторов на динамику изучаемого показателя.

Существует 3 метода исключения тенденции:

- Метод отклонений от тренда;

- Метод последовательных разностей;

- Включение в модель регрессии по временным рядам фактора времени.

1. ∆_yt = y_t – y_t-1 ; ∆_xt = x_t – x_t-1

∆_yt = a + b * ∆_xt

2. (y_t – y_t-1) = a + b*(x_t - x_t-1)

y_t = y_t-1 + a + b*(x_t - x_t-1)

y_p = y_n + a + b*(x_p – x_n)

y_p - прогнозное значение уровня ряда y_t;

y_n – конечный уровень динамического ряда y_t;

x_p - прогнозное значение уровня ряда х_t;

x_n - конечный уровень динамического ряда х_t.

40. Исключение тенденции на основе включения в модель регрессии по временным рядам фактора времени

Тенденция (T) – характеризует воздействие всех факторов на динамику изучаемого показателя.

Существует 3 метода исключения тенденции:

- Метод отклонений от тренда;

- Метод последовательных разностей;

- Включение в модель регрессии по временным рядам фактора времени.

1. y_t = a + b*x_t + c*t

y_t = a + b₁x₁ + b₂x₂ + b₃x₃ + c*t

2. P = aK^b1L^b2E^ct

lnP = lna + b₁ lnK + b₂ lnL +ct

y_t = a + bx₁ + ct + dt²

41. Автокорреляция в остатках. Критерий Дарбина-Уотсона в оценке качества уравнений, построенных по временным рядам

Автокорреляция в остатках - корреляционная зависимость. Это проблема. Последовательность остатков м. рассматриваться как временной ряд – возникает возможность построения зависимости последовательности остатков от времени. Остатки должны быть случайными (из МНК).

Причины А. остатков:

1. Связана с исходными данными и вызвана ошибками измерения в значениях результативного признака. Т,к. часто остатки содержат циклические колебания – каждое следующее значение остатков зависит от предшествующих.

2. Из-за недостатков формулировки модели.

а. м. отсутствовать фактор, оказывающий существенное воздействие на результат, влияние которого отражается в остатках. Помимо фактора времени – лаговые значения переменных (переменная появляется в модели с запозданием на неск. периодов; учитывающая запаздывание), включенных в модель.

б. м.б., что модель не учитывает несколько второстепенных по отдельности факторов, совместное влияние которых на результат уже оказывается существенным. Эта значимость проистекает в силу совпадения тенденций их изменения или фаз циклических колебаний.

r _ab = ((e_te_t-1)_cp – e_{t cp} * e_{t-1 cp}) / δ_etδ_et-1

d = Σ (e_t - e_t-1)² / Σe_t²

d = 2 * (1-r _ab) - (приблизительно); d = [0; 4]

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина — Уотсона:

1. выдвигается гипотеза об отсутствии автокорреляции остатков;

2. альтернативные гипотезы состоят в наличии положительной или отрицательной автокорреляции в остатках;

3. затем по специальным таблицам определяются критические значения критерия Дарбина — Уотсона для заданного числа наблюдений, числа независимых переменных модели и уровня значимости;

4. по этим значениям числовой промежуток разбивают на пять отрезков. (2 из этих отрезков образуют зону неопределенности; 3 - нет оснований отклонять гипотезу об отсутствии автокорреляции, есть положительная автокорреляция, есть отрицательная автокорреляция. При попадании в зону неопределенности практически считают, что имеется автокорреляция остатков, и поэтому отклоняют гипотезу о ее отсутствии).

42. Обобщенный метода наименьших квадратов (ОМНК) при построении модели регрессии по временным рядам

Невозможность или нецелесообразность использования традиционного МНК по причине проявляющейся в той или иной степени гетероскедастичности привели к разработке обобщенного метода наименьших квадратов (ОМНК). Фактически при этом корректируется модель, изменяются ее спецификации, преобразуются исходные данные для обеспечения несмещенности, эффективности и состоятельности оценок коэффициентов регрессии.

При нарушении гомоскедастичности и наличии автокорреляции (это статистическая корреляция между случайно распределенными в пространстве переменными одного и того же типа, атрибута, имени и т.д., когда корреляция зависит от расстояния и/или направления между местоположениями) рекомендуют заменять МНК на ОМНК.

Отличие: применяется к преобразованным данным и не только получает несмещенные оценки, но и оценки эти имеют меньшие выборочные дисперсии.

Порядок действий:

1. Преобразование исходных переменных:

y_t’ = y_t – r_b * y_t-1

x_t’ = x_t – r_b * x_t-1

2. Применение обычного МНК к уравнению и определение a* и b:

y_t’ = a’ + b*x_t’ + V_t

3. Расчет параметра a:

a = a’ / (1 - r_b)

4. Переход к исходному уравнению:

y_t = a + b*x_t + e_t

Вывод: Если в модели обнаружена гетероскедастичность, то ее можно устранить с помощью ОМНК. Все зависит от того, насколько точно мы можем оценить дисперсию ошибок наблюдений. Если мы нашли переменные, которые хорошо их описывают, то ОМНК будет работать.

Недостатки (две технические проблемы)

1. в преобразованной регрессии не будет константы, поэтому коэффициент детерминации перестает быть хорошим измерителем качества регрессии.

2. мы делим все переменные в уравнении регрессии на одну и ту же переменную, это может привести к возникновению ложных связей и мультиколлинеарности (тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат).

Последовательность формул:

1. y_t = a + b*x_t + e_t

y_t-1 = a + b*x_t-1 + e_t-1

e_t = c + d *e_t-1 + V_t

d = ((e_te_t-1)_cp – e_{t cp} * e_{t-1 cp}) / (e²_t-1cp – (e_{t-1 cp})²)

2. e_t = r*e_t-1 + V_t

y_t = a + b*x_t + r*e_t-1 + V_t

y_t-1 = a + b*x_t-1 + r*e_t-1 + V_t

r_b*y_t-1 = r_b*a + r_b*b*x_t-1 + r_b *e_t-1

3. y_t - r_b*y_t-1 = a - r_b*a + r_b*b*x_t-1 + e_t - r_b *e_t-1

y_t - r_b*y_t-1 = a(1 - r_b) + b(x_t - r_b*x_t-1) + (e_t - r_b *e_t-1)

y_t’ = a’ + b*x_t’ + V_t

43. Прогнозирование на основе рядов динамики

Временной (динамический) ряд – это ряд последовательно расположенных во времени числовых значений соответствующего показателя

Элементы временного ряда:

1. уровни ряда (y_t)- числовые значения того или иного показателя;

2. время (t).

Виды временных рядов:

1. моментные, если время задано моментами;

2. интервальные, если время задано интервалами.

Компоненты временного ряда:

1. Тенденция (T) – характеризует воздействие всех факторов на динамику изучаемого показателя.

2. Периодические колебания (P)

3. Случайные колебания (E)

y_t = f (T, P, E)

Статистический прогноз – вероятностная оценка возможностей развития объекта (процесса) и величины его признаков в будущем, полученная на основе статистической закономерности, выявленной по данным прошлого периода.

Назначение: а. планирование управления объекта; б. выработка стратегии поведения субъекта (если объект не управляем).

!!! Статистический прогноз предполагает не только верное качественное предсказание, но и достаточно точное количественное измерение вероятных возможностей ожидаемых значений признаков. Необходимо, чтобы прогностическая модель имела достаточную точность или допустимо малую ошибку прогноза.

Область применения – большое значения изучения трендов и колеблемости: а. в социально-экономических науках;

б. в процессе практического планирования и управления производством. Прогноз выражается в виде:

1. Точечный. Оценка прогнозируемого показателя в точке (в конкретном году, месяце, дне, середине периода прогноза) по уравнению, описывающему тенденцию показателя. Рассчитывается путем подстановки номера года, на который рассчитывается прогноз, в уравнение тренда. Она является средней оценкой для прогнозного интервала времени. Точечный прогноз указывает ту величину урожайности, на которую в среднем выйдет объект на прогнозируемый год, если тенденция динамики урожайности сохранится. Эту величину можно использовать в планирование.

2. Интервальный. По типу прогнозируемого показателя распадается на 3 вида:

- прогноз вероятных границ тренда;

- прогноз вероятных границ уровней отдельных лет с учетом их возможной -колеблемости относительно тренда;

- прогноз вероятных границ среднегодовых уровней динамического ряда.

Ур-ие тренда: y = a + bt; t – количество периодов до планового включительно.

44. Общая характеристика моделей с распределенным лагом и моделей авторегрессии

I. Лаговая переменная - переменная появляется в модели с запозданием на неск. периодов; учитывающая запаздывание.

Виды моделей:

1. модели с распределенными лагами (с лаговыми объясняющими переменными):

y_t = a + b₀x_t + b₁x_t-1 + … + e_t

2. модели авторегрессии (с лаговыми зависимыми переменными):

y_t = a + bx_t + c₁x_t-1 + c₂x_t-2 + … + e_t

3. авторегрессионные модели с распределенными лагами (модели с лаговыми зависимыми и независимыми переменными):

y_t = a + b₁y_t-1 + … + b_kу_t-k + c₀x_t + c₁x_t-1 + c₂x_t-2 + … + e_t

Модели с распределенными лагами:

1. с конечным числом лагов: y_t = a + b₀х_t + b₁x_t-1 + … + b_кx_t-к + + e_t

2. с бесконечным числом лагов: y_t = a + b₀х_t + b₁x_t-1+ b₂x_t-2 + … + e_t

Пример: y_{t с крыш} = a + b₀x_t + b₁x_t-1 + b₂x_t-2 + b₃x_t-3 + b₄x_t-4

Вывод: данная модель означает, что изменение во времени t объясняющей переменный x будет влиять на значения результативного признака y в течение 4-х следующих моментов времени.

II. Авторегрессия - применяемая в эконометрике модель для отыскания зависимости дисперсии текущей ошибки от квадратов ошибок модели для предшествующих наблюдений.

y_t = a + b₀x_t + n₁y_t-1 + e_t

- параметр b₀ характеризует краткосрочное изменение y_t под воздействием изменения x_t на 1 единицу.

- долгосрочный мультипликатор изменения y: b = b₀ / (1 – c₁)

45. Интерпретация параметров моделей с распределенным лагом и моделей авторегрессии

I. Лаговая переменная - переменная появляется в модели с запозданием на неск. периодов; учитывающая запаздывание.

Модели с распределенными лагами:

1. с конечным числом лагов: y_t = a + b₀х_t + b₁x_t-1 + … + b_кx_t-к + + e_t

2. с бесконечным числом лагов: y_t = a + b₀х_t + b₁x_t-1+ b₂x_t-2 + … + e_t

Пример: y_{t с крыш} = a + b₀x_t + b₁x_t-1 + b₂x_t-2 + b₃x_t-3 + b₄x_t-4

Вывод: данная модель означает, что изменение во времени t объясняющей переменный x будет влиять на значения результативного признака y в течение 4-х следующих моментов времени.

Параметры:

1. Краткосрочный мультипликатор. Коэффициент b₀. Он характеризует среднее изменение результата y при изменении на 1 единицу своего измерения в фиксированный момент времени t.

2. Промежуточные мультипл-ры. В момент времени t+1 воздействие объясняющей переменной x на результат y составит (b₀+b₁) единиц, а в момент времени t+2 общее изменение y составит (b₀+b₁+b₂) единиц.

- b₀+b₁ - изменение y в момент времени t+1;

- b₀+b₁+b₂ - изменение y в момент времени t+2.

3. Долгосрочный мультипл-р. При k=4 долгосрочный мультипликатор составит b₀+b₁+b₂+b₃+b₄. Он характеризует общее среднее изменение y через 4 временных интервала при увеличении x в момент времени t на 1 единицу

- Σb_i

4. Относительные коэффициенты модели. Характеризует долю общего изменения y в момент времени t+i.

ß_i = b_i / Σb_i ; Σb_i = 1; b_i = [0; 1]

5. Средняя величина лага. Показывает средний интервал времени, в течение которого будет происходить изменение зависимой переменной y под воздействием изменения объясняющей переменной x в момент времени t.

Чем меньше величина среднего лага, тем быстрее реагирует результат y на изменение x. И наоборот, высокое значение среднего лага показывает, что воздействие объясняющей переменной на результат будет сказываться с течением длительного промежутка времени.

i _ср = Σ(i * ß_i)

6. Медианный лаг. Тот период времени, в течение которого с момента времени t будет реализована половина общего эффекта воздействия объясняющей переменной x на результат y.

Σß_i = 0,5

II. Авторегрессия - применяемая в эконометрике модель для отыскания зависимости дисперсии текущей ошибки от квадратов ошибок модели для предшествующих наблюдений.

y_t = a + b₀x_t + n₁y_t-1 + e_t

- параметр b₀ характеризует краткосрочное изменение y_t под воздействием изменения x_t на 1 единицу.

- долгосрочный мультипликатор изменения y: b = b₀ / (1 – c₁)

46. Применение фиктивных переменных для моделирования сезонных колебаний

Фиктивная (структурная) переменная – переменная, принимающая значение 1 или 0. Их количество д.б на 1 меньше, чем количество моментов времени за 1 цикл колебания.

Используется при решении следующих задач:

1. при моделировании качественных признаков;

2. для учета структурной неоднородности, к которой приводят качественные признаки;

3. для оценки сезонных колебаний.

Каждая фиктивная переменная отражает сезонную компоненту временного ряда для 1 периода. Она = 1 для 1 периода и = 0 для всех остальных.

Рассмотрим временной ряд, содержащий циклический колебания периодичностью К:

y_t = a + bt + c₁x₁ + … + c_jx_j + … + c_k-1x_k-1 + e_t

где х_j = 1 для j внутри цикла и х = 0 для остальных.

Для моделирования сезонных колебаний на основе поквартальных данных за несколько лет, число кварталов = К = 4, общий вид модели:

y_t = a + bt + c₁x₁ + c₂x₂ + c₃x₃ + e_t

где х₁ = 1 для 1 квартала и х = 0 для остальных; х₂ = 1 для 2 квартала и 0 для остальных; … .

Уравнение тренда для каждого квартала будет:

1. y_t = a + bt + c₁ + e_t

2. y_t = a + bt + c₂ + e_t

3. y_t = a + bt + c₃ + e_t

4. y_t = a + bt + e_t

Т.о. фиктивный переменные позволяют дифференцировать величину свободного члена уравнения регрессии для каждого квартала:

1. a + c₁

2. a + c₂

3. a + c₃

4. a

Параметр b характеризует среднее абсолютное изменение уровней ряда под воздействием тенденции. Это аналог аддитивной модели, т.к. фактический уровень врем. ряда – сумма трендовой, сезонной и случ. компонент.

Тенденция (T) – характеризует воздействие всех факторов на динамику изучаемого показателя.

47. Общее понятие о системах уравнений, используемых в эконометрике

Объект стат. изучения – сложные системы. Отдельное ур-ие не может характеризовать влияние признака на вариацию полностью. Поэтому используем систему уравнений, чтобы лучше описать структуру связей между переменными.

1. Система независимых уравнений (зависимая переменная у рассматривается как функция одного и того же набора факторов х):

y₁ = a₀₁ + a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + e₁

y₂ = a₀₂ + a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + e₂

y₃ = a₀₃ + a₃₁x₁ + a₃₂x₂ + a₃₃x₃ + e₃

2. Система рекурсивных уравнений (если зависимая переменная у одного ур-ия выступает в виде фактора х в другом уравнении):

y₁ = a₀₁ + a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + e₁

y₂ = a₀₂ + b₂₁y₁ + a₂₂x₂ + e₂

y₃ = a₀₃ + b₃₁y₁ + b₃₂y₂ + a₃₄x₄ + a₃₅x₅ + e₃

3. Система взаимозависимых уравнений (одни и те же зависимые переменные входят в левую часть, в других уравнениях – в правую):

y₁ = a₀₁ + b₁₂y₂ + a₁₁x₁ + a₁₂x₂ + e₁

y₂ = a₀₂ + b₂₁y₁ + b₂₃y₃ + a₂₃x₃ + e₂

y₃ = a₀₃ + b₃₂y₂ + a₃₃x₃ + e₃

а. Статистическая модель Кейнса для описания народного хозяйства страны в наиболее простом варианте (С – личное потребление, у – национальный доход, I – инвестиции (все в постоянных ценах)):

С = α + ßy + e

Y = C + I

б. Модель цены и зарплаты:

w = a₁ + b₁₁UN + b₁₂P + e₁

p = a₂ + b₂₁w + b₂₂R + b₂₃M + e₂

w – зарплата; UN – уровень безработицы; P – темп уровня цен; R – темп изменения постоянного капитала; M – темп изменения цен на импортируемое сырье.

48. Виды переменных в системах взаимозависимых уравнений

Система взаимозависимых (одновременных) уравнений:

y₁ = a₀₁ + b₁₂y₂ + a₁₁x₁ + a₁₂x₂ + e₁

y₂ = a₀₂ + b₂₁y₁ + b₂₃y₃ + a₂₃x₃ + e₂

y₃ = a₀₃ + b₃₂y₂ + a₃₃x₃ + e₃

Зависимая переменная одного уравнения может появляться одновременно в виде переменной (но уже в качестве независимой) в одном или нескольких других уравнениях. Поэтому теряет смысл традиционное различение зависимых и независимых переменных. Устанавливается различие между двумя видами переменных:

1. совместно зависимые переменные (эндогенные), влияние которых друг на друга должно быть исследовано;

2. предопределенные переменные - оказывают влияние на первые, однако не испытывают их воздействия:

а. то переменные с запаздыванием (лаговые);

б. определенные вне данной системы уравнений экзогенные переменные. Примеры:

Экзогенные - показатели климатических условий, если они включаются в модель.

Экономические переменные в зависимости от задач и структуры модели могут относиться и к эндогенным, и к экзогенным.

!!! В зависимости от характера переменных, эконометрические модели классифицируются на линейные модели с одной, двумя и большим числом переменных, а также на пробит-модели, логит-модели, тобит-модели.

49. Структурная и приведенная формы модели.

Структурная:

y₁ = a₀₁ + b₁₂y₂ + a₁₁x₁ + a₁₂x₂ + e₁

y₂ = a₀₂ + b₂₁y₁ + b₂₃y₃ + a₂₃x₃ + e₂

y₃ = a₀₃ + b₃₂y₂ + a₃₃x₃ + e₃

Приведенная:

y₁ = А₁ + В₁₁x₁ + В₁₂x₂ + В₁₃x₃ + V₁

y₂ = A₂ + B₂₁x₁ + B₂₂x₂ + B₂₃x₃ + V₂

y₃ = A₃ + B₃₁x₁ + B₃₂x₂ + B₃₃x₃ + V₃

а. для модели Кейнса (равновесие спроса и предложения):

С = А₁ + В₁I + V₁

Y = A₂ + B₂I + V₂

б. для модели цены и зарплаты:

w = A₁ + B₁₁UN + B₁₂R + B₁₃M + V₁

p = A₂ + B₂₁UN + B₂₂R + B₂₃M + V₂

w – зарплата; UN – уровень безработицы; P – темп уровня цен; R – темп изменения постоянного капитала; M – темп изменения цен на импортируемое сырье.

Особенности приведенной формы:

1. в правой части модели используется только предопределенные переменные, следовательно расчет параметров может быть произведен с помощью обычного МНК;

2. существует определенное соотношение между коэффициентами структурной формы и приведенной формы (приведенные коэффициенты – нелинейные соотношения коэффициентов структурной моделей).

Связь между структурными приведенными коэффициентами (в модели Кейнса):

Модель Кейнса: С = α + ßy + e

Y = C + I

- С = α + ß(С +I) + e

C – ßС = α + ßI + e

C = α /(1-ß) + ßI/(1-ß) + e /(1-ß)

- A = α /(1-ß); B₁₁= ßI/(1-ß); V₁ = e /(1-ß)

- C = A₁ +B₁₁I + V₁

- y = y /(1-ß) + I/(1-ß) + e /(1-ß)

y = A₂ +B₂₁I + V₂

50. Проблема идентификации Необходимое условие идентификации (порядковое или счетное правило)

Структурная:

y₁ = a₀₁ + b₁₂y₂ + a₁₁x₁ + a₁₂x₂ + e₁

y₂ = a₀₂ + b₂₁y₁ + b₂₃y₃ + a₂₃x₃ + e₂

y₃ = a₀₃ + b₃₂y₂ + a₃₃x₃ + e₃

Приведенная:

y₁ = А₁ + В₁₁x₁ + В₁₂x₂ + В₁₃x₃ + V₁

y₂ = A₂ + B₂₁x₁ + B₂₂x₂ + B₂₃x₃ + V₂

y₃ = A₃ + B₃₁x₁ + B₃₂x₂ + B₃₃x₃ + V₃

Идентификация модели – соответствие между приведенной и структурной формами модели, позволяющее однозначно оценить структурные коэффициенты по приведенным коэффициентам модели.

Случаи идентификации:

1. Модель идентифицируема, если число коэффициентов структурной модели равно числу коэффициентов приведенной модели и структурные коэффициенты однозначно определяются по приведенным коэффициентам.

2. Модель неидентифицируема, если число структурных коэффициентов больше числа приведенных коэффициентов. Модели, в которых в каждом уравнении системы участвуют все эндогенные и экзогенные переменные, имеющиеся в системе, всегда неидентифицируемы.

3. Модель сверхидентифицируема, если число приведенных коэффициентов превышает число структурных коэффициентов. В результате на основе коэффициентов приведенной модели можно получить несколько значений одного структурного коэффициента.

Неидентифицируемая система - если хотя бы 1 ур-ие системы неидентифицируемо; система не решается.

Сверхидентифицируемая система – если хотя бы 1 ур-ие системы сверхидентифицируемо.

Необходимое условие идентификации (порядковое или счетное правило):

1. ур-ие идентифицируемо: D+1=H

2. ур-ие неидентифицируемо: D+1<H

3. ур-ие сверхидентифицируемо: D+1>H

D – число предопределенных переменных, отсутствующих в проверяемом ур-ии, но присутствующих в других ур-ях системы; H – число эндогенных переменных в проверяемом ур-ии.

Пример - проверка на идентификацию (структурная форма модели):

y₁ = b₁₂y₂ + b₁₃y₃ + a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + e₁

y₂ = b₂₁y₁ + b₂₃y₃ + a₂₁x₁ + a₂₁x₂ + a₂₃x₃ + e₂

y₃ = b₃₁y₁ + b₃₂y₂ + a₃₁x₁ + a₃₂x₂ + a₃₃x₃ + e₃

1 ур-ие неидентифицируемо: 0+1< 3, D+1<H

2 ур-ие неидентифицируемо: 0+1< 3, D+1<H

3 ур-ие неидентифицируемо: 0+1< 3, D+1<H

51. Достаточное (ранговое) условие идентификации

Чтобы уравнение, входящие в систему одновременных уравнений было идентифицировано, необходимо и достаточно:

1. чтобы ранг матрицы коэффициентов по отсутствующим в нем переменным был на единицу меньше числа эндогенных переменных в системе;

2. определитель матрицы не был равен нулю.

D+1=H

D – число предопределенных переменных, отсутствующих в проверяемом ур-ии, но присутствующих в других ур-ях системы; H – число эндогенных переменных в проверяемом ур-ии.

y₁ = A₁ + b₁₂y₂ + b₁₃y₃ + a₁₁x₁ + a₁₂x₂ + e₁

y₂ = A₂ + b₂₁y₁ + a₂₂x₂ + a₂₃x₃ + a₂₄x₄ + e₂

y₃ = A₃ + b₃₁y₁ + b₃₂y₂ +a₃₁x₁ + a₃₂x₂+ e₃

1. Первое уравнение: Н=3 и D=2, т. е. D+1=H.

Коэфф. при отсутствующих в 1 ур-ии переменных:

уравнения	переменные
	х3	х4
II	а23	а24
III	0	0

- определитель матрицы (detA) коэффициентов равен 0. Достаточное условие идентификации не выполняется;

- уравнение неидентифицируемо.

2. Второе уравнение: Н=2 и D=1, т.е. D+1=Н.

уравнения	переменные
	у3	х1
I	b23	а11
III	-1	а31

- detA ≠ 0, ранг матрицы равен 2. Достаточное условие идентификации выполняется;

- уравнение точно идентифицировано.

3. Третье уравнение: Н=3 и D=2, т.е. D+1=Н.

уравнения	переменные
	х3	х4
I	0	0
II	а23	а24

- detA=0. Достаточное условие идентификации не выполняется;

- уравнение не идентифицировано.

52. Косвенный метод наименьших квадратов для оценки параметров структурной формы модели

Оценивание параметров в структурной форме моделей:

- косвенный МНК (КМНК);

- двухшаговый МНК (ДМНК).

КМНК:

1. Строится приведенная форма модели.

2. Для каждого уравнения приведенной модели традиционным МНК оцениваются параметры модели.

3.Коэффициенты приведенной модели трансформируются в параметры структурной модели.

Пример КМНК для оценки параметров структурной модели:

y₁ = a₀ + а₁y₂ + a₂x₁ + e₁

y₂ = b₀ + b₁y₁ + b₂x₂ + e₂

y1	y2	x1	x2
2	6	1	4
3	7	2	2
4	8	3	3
5	9	2	6
6	6	4	7

- Приведенная форма модели

y₁ = A₁ + B₁₁X₁ + B₁₂X₂ + V₁

y₂ = A₂ + B₂₁X₁ + B₂₂X₂ + V₂

- A₁=0,3 B₁₁=0,8 B₁₂=0,35

A₂=7,3 B₂₁=-0,1 B₂₂=-0,005

- y_{1 с крыш} = 0,3 + 0,8х₁ + 0,35х₂

y_{2 с крыш} = 7,3 – 0,1х₁ – 0,005х₂

- Выражаем х₁ из 2 ур-ия и х₂ из 1 ур-ия. Затем эти х подставляем в ур-ия.

- Т.о.: y₁ = 495 – 66у₂ – 3х₁

y₂ = 7 – 0,08у₁ + 0,02х₂

53. Двухшаговый метод наименьших квадратов для оценки параметров структурной формы модели

Оценивание параметров в структурной форме моделей:

- косвенный МНК (КМНК);

- двухшаговый МНК (ДМНК).

ДМНК:

1. Первый шаг – построение приведенной формы модели (ПФМ). С помощью МНК находят числовые параметры каждого уравнения ПФМ.

2. Второй шаг - для каждого уравнения структурной формы модели (СФМ) выполняют следующие действия:

а. находят эндогенные переменные, являющиеся факторными признаками (стоят в правой части уравнения);

б. для этих переменных определяют их выровненные (теоретические) значения, используя соответствующие уравнения ПФМ;

в. находят параметры рассматриваемого уравнения СФМ обычным МНК, заменяя исходные значения эндогенных переменных-факторов их выровненными значениями.

54. Применение систем эконометрических уравнений

Под системой э. ур-ий обычно понимается система одновременных, совместных уравнений. Построение системы структурных уравнений позволяет глубже изучить причины связи результирующих признаков. При этом происходит выделение и оценка косвенных и непосредственных влияний признаков.

Применение:

1. Для построения макроэкономических моделей функционирования экономики разных стран. Большинство – это мультипликативные модели кейнсианского типа с разной степенью сложности.

а. Статистическая модель Кейнса для описания народного хозяйства страны в наиболее простом варианте:

С = α + ßy + e

Y = C + I   

где С – личное потребление, у – национальный доход, I – инвестиции (все в постоянных ценах).

б. динамическая модель Кейнса:

С_t = a + b₁Y_t + b₂Y_t-1 + e

Y_t = C_t +G_t + I_t + L_t  

P_t = Y_t + Z_t.

где  У_t, С_t, P_t - доход, частное потребление, ВНП в период времени t;

У_t-1 - доход предыдущего года;

G_t, I_t, L_t, Z_t - общественное потребление, валовые капиталовложения, изменения складских запасов, сальдо платежного баланса.

2. Для исследования спроса и предложения:

Q^d = a₀ + a₁P + e₁

Q^s = b₀ + b₁P + e₁

Q^d = Q^s

где Q^d и Q^s - объем спроса и объем предложения,  Р - цена.