2. Мгновенный и непрерывный линейный источник тепла.

Отмечая универсальность функции (2), подчеркнём, что эта функция является фундаментальным решением (1) и описывает температурное поле в любой точке трёхмерного пространства. Очевидно, что мгновенный линейный источник тепла можно рассматривать как совокупность бесчисленного множества точечных источников, расположенных на некоторой прямой. Таким образом, суммируя действие множества мгновенных точечных источников, найдём выражение для мгновенного линейного источника тепла. Аналитически операция сводится к интегрированию (2) по в пределах от до (предполагается, что источник расположен на прямой, параллельной оси z и проходящей через точку с координатами x₁, y₁), т.е.

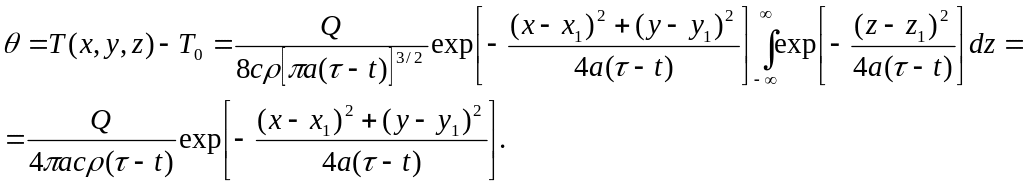(9)

При вычислении интеграла сделана замена и использовано соотношение (4).

Вводя , , перепишем (9) в виде

(10)

Выражение (10) неудобно для практических расчётов, т.к. кроме теплопроводности, неизвестной величиной является и температуропроводность. Следует также учесть, что мгновенный тепловой источник — математическая абстракция. На практике «мгновенность» реализуется путём задания кратковременного теплового импульса. Такой импульс может быть создан, например, за счёт действия электрического или лазерного источника. Необходимо, таким образом, рассматривать задачу о действии источника в течение некоторого времени (в формуле (10) — время, через которое наблюдается действие мгновенного источника, но не длительность импульса). Для теоретического решения этой задачи нужно произвести «суммирование» действия мгновенного линейного источника (10) во времени, т.е. интегрировать (10) по в пределах от 0 до :

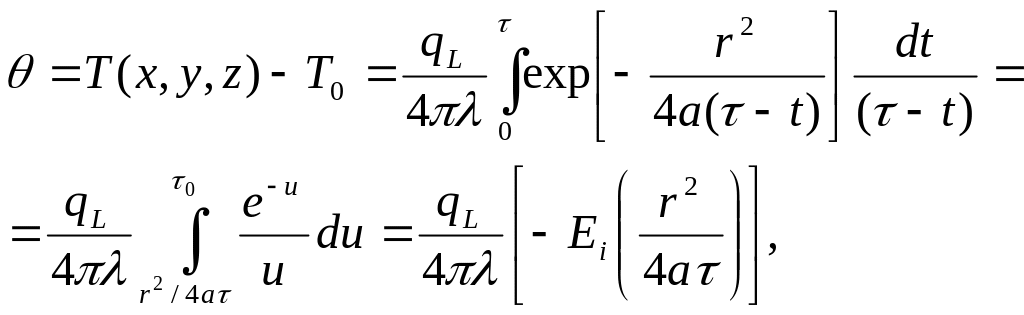(11)

где — интегральная показательная функция, таблицы которой можно найти в работе [3]. Разложение функции имеет вид

(12)

где — постоянная Эйлера.

Таким образом, решение (11) можно написать так:

(13)

где — локальное число Фурье. При больших значениях приближённо имеем:

(14)

Решения (13) и (14) могут быть использованы для определения теплофизических характеристик, если постоянный нагрев неограниченного тела осуществляется бесконечно тонкой проволокой с малым температурным коэффициентом сопротивления.

3. Вывод расчётных формул для определения теплофизических характеристик методом импульсного линейного источника тепла.

Интегрирование (10) по времени не налагает каких-либо ограничений на величину времени, т.е. на продолжительность теплового воздействия. Если источник действует достаточно долго, то мы не получим кривую, изображённую на рис.1. Температура в некоторой точке будет монотонно расти в соответствии с соотношением (13). Чтобы получить экспериментально кривую, подобную изображённой на рис.1, необходимо задать короткий тепловой импульс (см. п.2). Идея метода и состоит в исследовании экспериментальной зависимости на экстремум, если эта зависимость является результатом кратковременного (импульсного) теплового воздействия. Перепишем (11), подставив в верхнем пределе интегрирования вместо . Пусть эта формальная замена подчёркивает кратковременность действия источника

(15)

где ; .

Значение максимума избыточной температуры в точке будет соответствовать определённому моменту времени

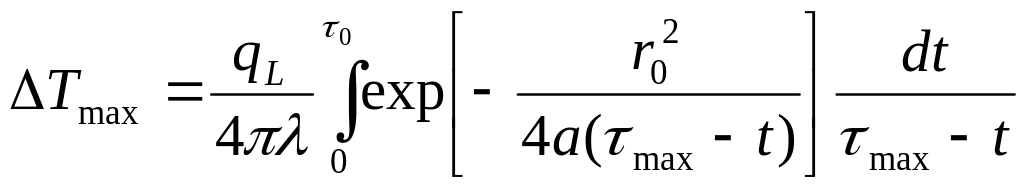. (16)

Если продифференцировать выражение (16) по и приравнять производную нулю, то получим соотношение, при котором должно выполняться условие экстремума:

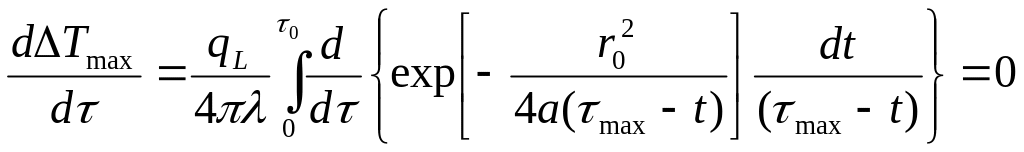(17)

(в дальнейшем будем писать вместо ).

Далее всё сводится к преобразованию (17)

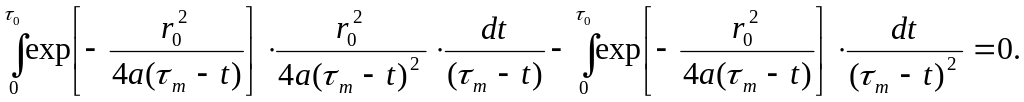(18)

Введём обозначение и сделаем замену:

; .

Тогда соотношение (18) можно переписать в виде

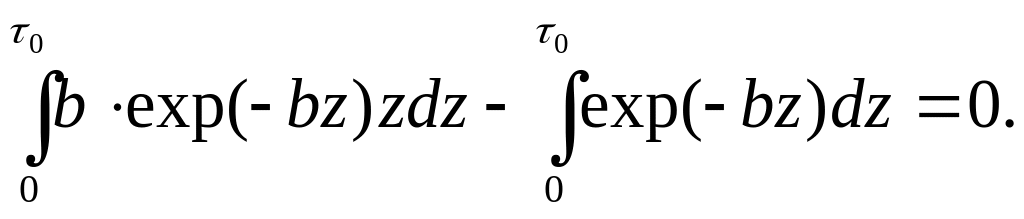(19)

Интегрируя первый интеграл (19) по частям, получим:

Следовательно,

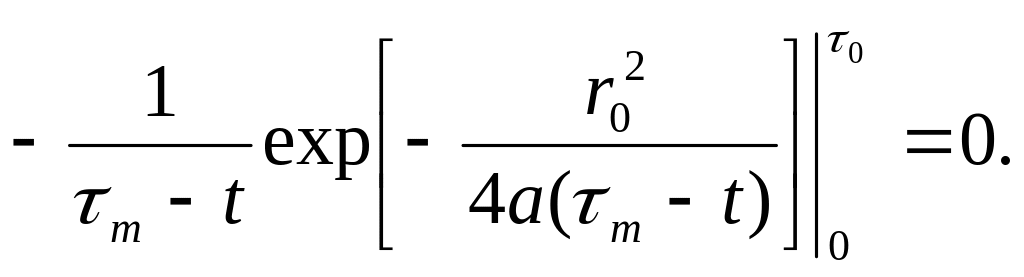
Последнее соотношение можно переписать в виде

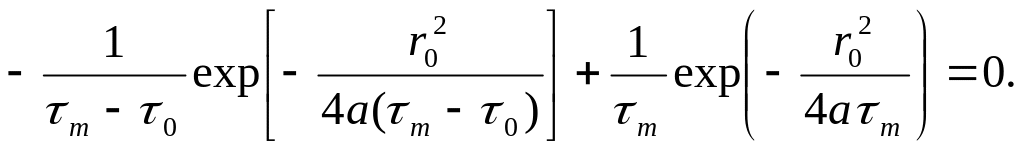
Логарифмируя, найдём, что

(20)

Введём обозначение:

(21)

Тогда (20) запишется в виде

(22)

Выражение (22) связывает температуропроводность с экспериментально определяемыми величинами. Формула для расчёта коэффициента теплопроводности получается путём преобразования (15):

Дальнейшие выкладки аналогичны приведённым в п.2 с учётом выражения (22). Введём переменную

Тогда

Так как изменяется в пределах от до , то новые пределы интегрирования будут:

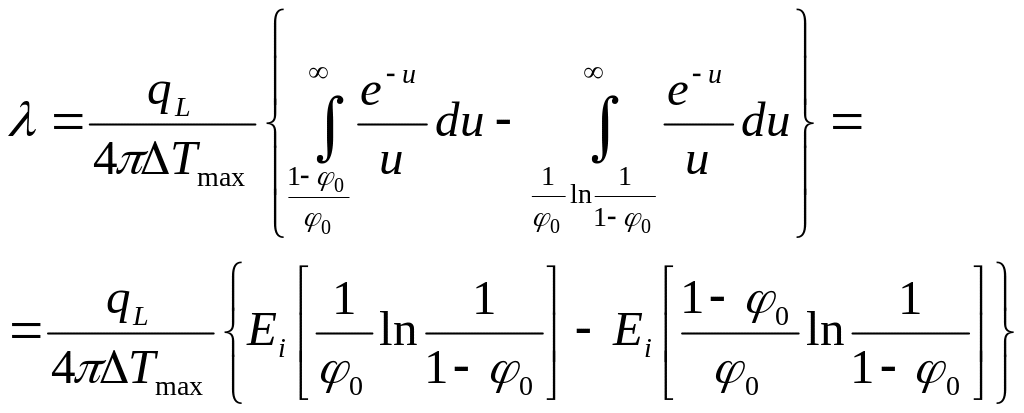
(23)

где .

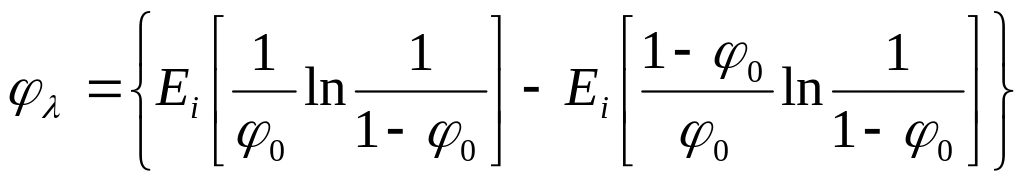Таким образом, коэффициент теплопроводности определяется по формуле (23). Коэффициент температуропроводности на основании (22):

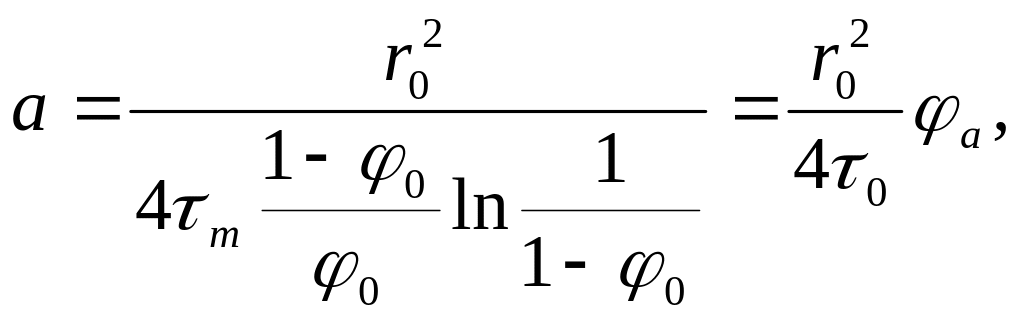(24)

где .

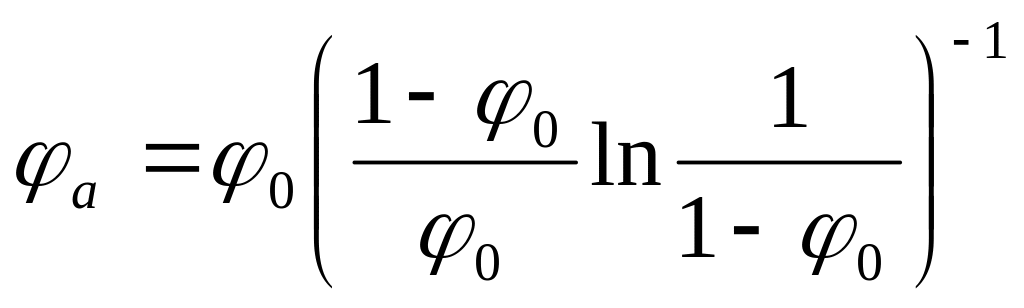Теплоёмкость вычисляется по формуле

, (25)

где — плотность материала образца.

Значения и приведены в таблице, данной в приложении.