БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Физический факультет

Кафедра энергофизики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторной работе «ИССЛЕДОВАНИЕ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ИМПУЛЬСНЫМ МЕТОДОМ»

Минск 2009

ИССЛЕДОВАНИЕ ТЕПЛОВИЗИЧЕСКИХ ХАРАКТЕРИСТИК

ИМПУЛЬСНЫМ МЕТОДОМ

1. Общие теоретические основы метода мгновенного источника тепла.

Закономерности развития нестационарных температурных полей, создаваемых действием мгновенных точечных, линейных или плоских источников тепла в неограниченном теле, явились аналитической основой для создания импульсных методов комплексного определения теплофизических характеристик различных материалов.

Первое представление о мгновенном точечном источнике тепла, т.е. о конечном количестве тепла, мгновенно выделяемом в заданной точке неограниченного тела в определённый момент времени, встречается в работе Кельвина. Несколько позже метод мгновенных источников получил большое развитие и практическое приложение к конкретным задачам теплопроводности в трудах Г. Карслоу, Д. Егера, А.В. Лыкова, А.Ф. Чудновского [1,2].

Общее решение дифференциального уравнения теплопроводности

(1)

для случая действия мгновенного точечного источника тепла в точке (x₁, y₁, z₁) неограниченного тела удовлетворяет функции

(2)

где T₀=const — начальная температура неограниченного тела, постоянная во всех его точках; a, c и — соответственно температуропроводность, удельная теплоёмкость и плотность тела; — время; t — начальный момент времени; Q — количество тепла (Дж), выделяемое в точке (x₁, y₁, z₁) неограниченного тела в момент времени .

В начальный момент времени значение (1) равно нулю везде, кроме точки с координатами (x₁, y₁, z₁), в которой функция (2) стремится к бесконечности. Очевидно, должно выполняться равенство

, (3)

так как

; (4)

Таким образом, особенность функции источника состоит ещё и в том, что количество тепла, выделяемое во всём объёме в любой момент времени , будет постоянным и равным Q, т.е. количеству тепла, мгновенно выделяемого в начальный момент времени в точке (x₁, y₁, z₁). Следует понимать, что в момент времени тепловое влияние распространяется на всю область пространства, но значение (2) будет сохранять максимум в точке (x₁, y₁, z₁) теоретически во всём временном интервале выравнивания температуры по объёму тела. Однако «высота» максимума будет непрерывно уменьшаться, стремясь в пределе к нулю.

Из выражения (2) можно найти, что температура в точке, находящейся на расстоянии , достигает максимальной величины в момент времени, определяемый этим расстоянием и коэффициентом температуропроводности. Для этого (2) необходимо исследовать на максимум (проделать самостоятельно). В итоге найдём, что

. (5)

Следовательно,

. (6)

При реализации соответствующей экспериментальной схемы соотношение (5) может быть использовано для расчёта коэффициента температуропроводности.

Построение графической зависимости (2) затруднительно, т.к. эта функция содержит большое количество параметров и переменных. Целесообразно поэтому ввести безразмерные комплексы и параметры, что обычно и делается при изучении явлений переноса. Введём число (критерий) Фурье

.

Тогда функцию (2) можно записать в виде

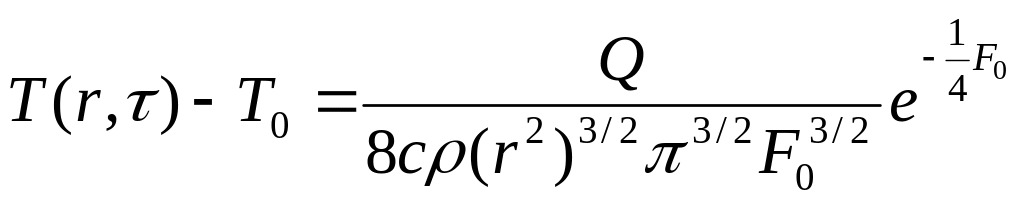. (7)

Дальнейшее преобразование (7) даёт следующее выражение:

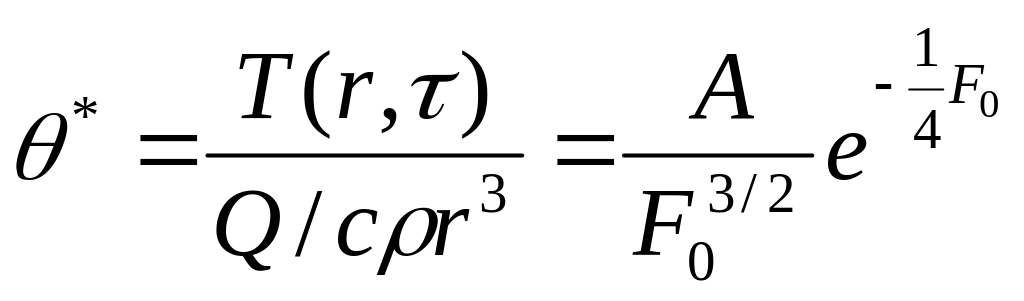, (8)

где .

Зависимость (8) приведена на рис.1.

Следует отметить универсальность функции (2). Например, если проинтегрировать выражение (2) по соответствующим координатам, то нетрудно получить уравнения для мгновенных и непрерывных линейных, плоских, сферических или цилиндрических поверхностных источников тепла. Так как в дальнейшем нами будет использоваться линейный источник тепла, рассмотрим более подробно теорию этого источника.