
3.4 Канонічні форми запису лінійних рівнянь зі сталими
коефіцієнтами
У випадку двох незалежних змінних лінійне рівняння зі сталими коефіцієнтами має вигляд
![]() (3.23)
(3.23)
Йому відповідає характеристичне рівняння зі сталими коефіцієнтами. Тут характеристиками є прямі
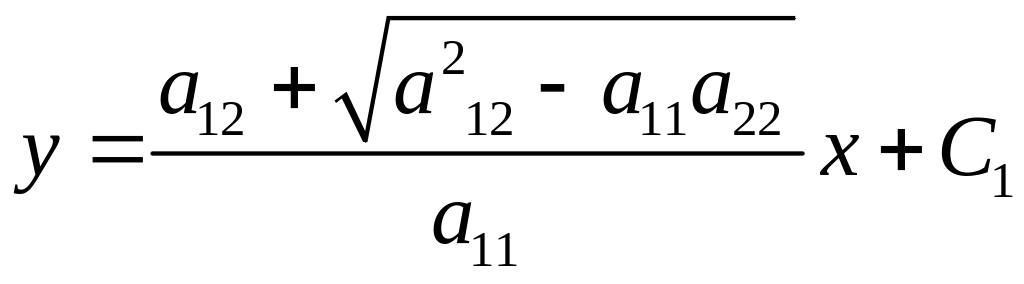 ;
;
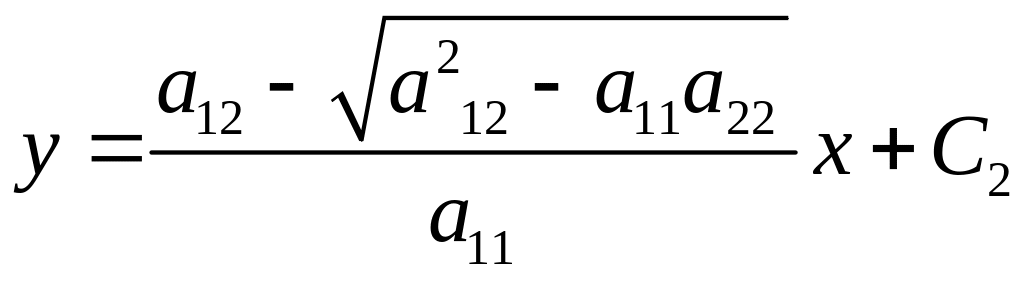 .
.
За допомогою відповідного перетворення змінних рівняння (3.23) приводиться до однієї з канонічних форм.
![]() -
еліптичний тип, (3.24)
-
еліптичний тип, (3.24)
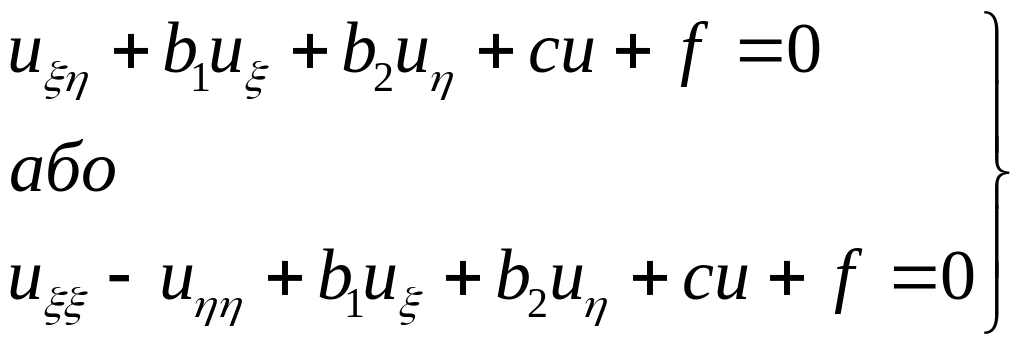 -
гіперболічний тип, (3.25)
-
гіперболічний тип, (3.25)
![]() - параболічний
тип.
(3.26)
- параболічний
тип.
(3.26)
Для
подальшого спрощення введемо замість
![]() нову
функцію
нову
функцію
![]()
![]() (3.27)
(3.27)
де
![]() і
і
![]() -
невизначені поки що параметри. Параметри
і
вибираються таким чином, щоб два
коефіцієнти, наприклад, при перших
похідних, перетворилися на нуль (
-
невизначені поки що параметри. Параметри
і
вибираються таким чином, щоб два
коефіцієнти, наприклад, при перших
похідних, перетворилися на нуль (![]() -
-![]() ,
,
![]() -
-![]() ,).
Тоді канонічні форми (3.24)-(3.26) будуть
мати вигляд
,).
Тоді канонічні форми (3.24)-(3.26) будуть
мати вигляд
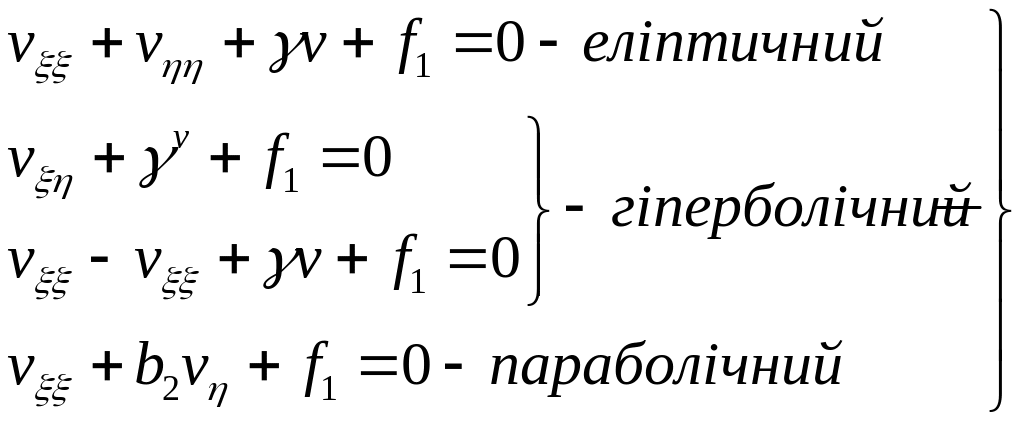 (3.28)
(3.28)
Приклад 3.3 Звести до канонічного вигляду рівняння
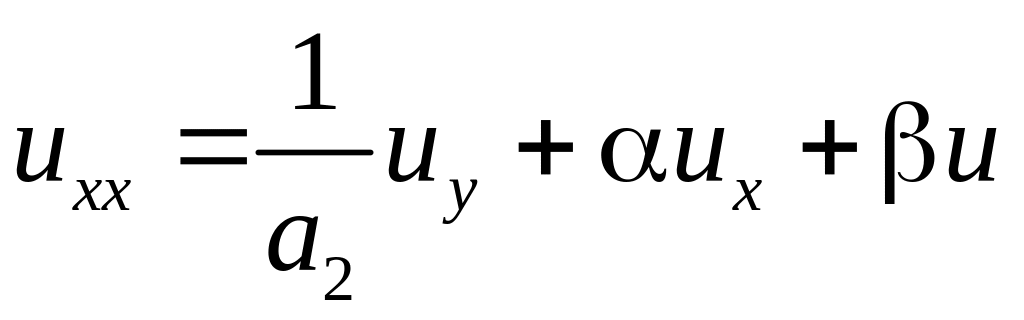
![]()
Розв’язок.
Скориставшись формулою (3.23) та зробивши
заміну
![]() ,
де
,
де
![]() - невизначені коефіцієнти. Будемо мати
- невизначені коефіцієнти. Будемо мати
![]() ,
,
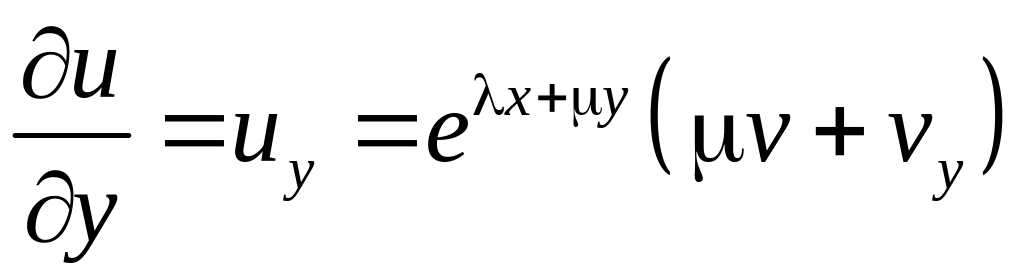 ,
,
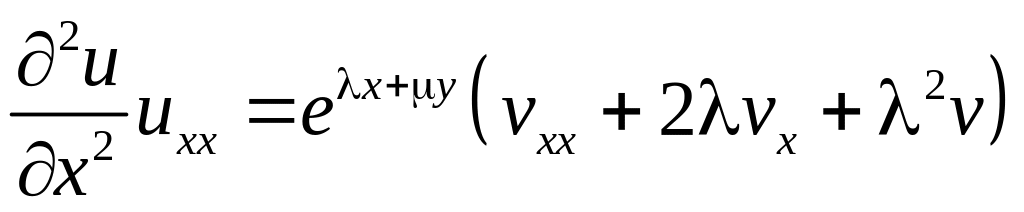 ,
,
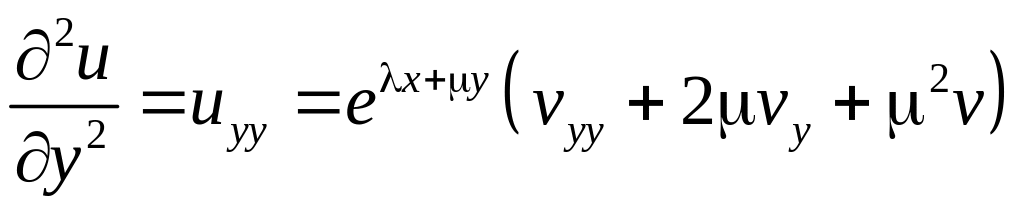 .
.
Підставивши
значення частинних похідних до рівняння
та скоротивши на
![]() ,
отримаємо
,
отримаємо
![]() .
.
Привівши подібні члени, будемо мати
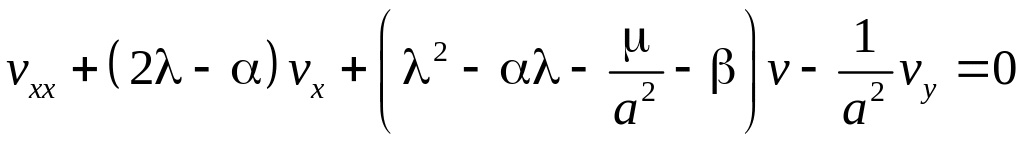 .
.
Визначаємо
![]() та
та
![]() так, щоб коефіцієнти при
так, щоб коефіцієнти при
![]() та
та
![]() оберталися на нуль.
оберталися на нуль.
 ,
,
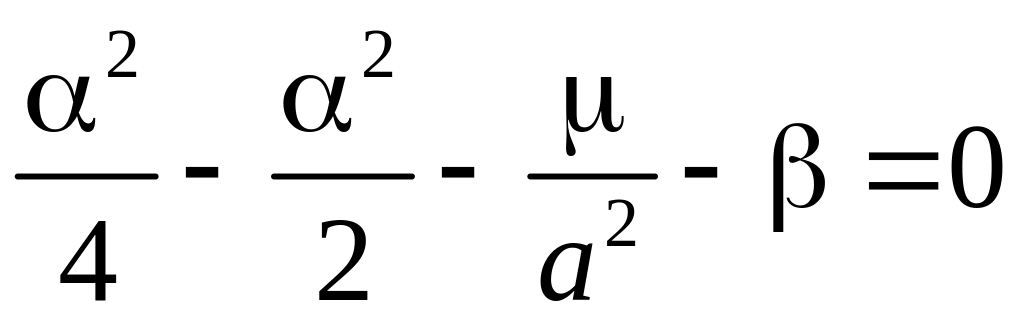 .
.
При таких значеннях та рівняння перетвориться на наступне
![]()
Ми отримали канонічне рівняння параболічного типу.
3.5 Крайові задачі
Основною задачею рівнянь з частинними похідними є математичне дослідження дослідження розв’язків рівнянь, визначення умов існування єдиного розв’язку, розробка методів розв’язку. У математичній фізиці розглядаються дві проблеми – пряма та обернена.
Різні типи диференціальних рівнянь описують різні з фізичної точки зору процеси. Для описання конкретного фізичного процесу необхідно крім самого рівняння, задати початковий стан цього процесу (початкову умову ) і режим на межі (граничні умови). Математично це пов’язано з відсутністю єдиного розв'язку диференціальних рівнянь. Додаткові умови, які дозволяють описати конкретний процес, називаються крайовими умовами (початкові і граничні крайові умови).
Розрізняють три основних типа крайових задач для диференціальних рівнянь другого порядку з частинними похідними.
1. Задачі
Коші для рівнянь гіперболічного та
параболічного типів: задаються початкові
умови, область
співпадає з усім простором
![]() ,
граничні умови відсутні.
,
граничні умови відсутні.
2. Крайова
задача для рівнянь еліптичного типу:
задаються граничні умови на межі
![]() ,
початкові умови відсутні.
,
початкові умови відсутні.
3. Мішана задача для рівнянь гіперболічного типу: задаються початкові та граничні умови.
Розрізняють три типи граничних умов.
Умова
I роду
![]() – на межі
області
задана функція,
– на межі
області
задана функція,
Умова
II роду
![]() – на межі області задана нормальна
похідна,
– на межі області задана нормальна
похідна,
Умова
III
роду
![]() – на межі області задана комбінація
нормальної похідної та функції.
– на межі області задана комбінація
нормальної похідної та функції.
