2.4 Задача Коші

Як і звичайне, диференціальне рівняння - рівняння з частинними похідними, має нескінченну множину розв’язків. Задача визначення розв’язку для рівнянь (2.2), (2.6) з додаванням початкових умов дозволяє знайти єдиний розв’язок. На відміну від початкової умови для звичайного диференціального рівняння, де задається значення функції в точці – для рівняння з частинними похідними необхідно знайти інтегральну поверхню рівняння (2.2), (2.6) яка проходить через задану криву у просторі

Задача Коші для рівняння (2.2), (2.6) зазавичай розуміється як задача визначення інтегральної поверхні, що проходить через задану лінію .

Нехай рівняння лінії задано параметрично . Прийнявши координати точок кривої за початкові умови для отримаємо розв’язок системи (2.9) у вигляді

, або для

(2.15)

Для розв'язання задачі Коші проводять через кожну точку кривї характеристичну криву, тобто інтегральну криву системи (2.9). При цьому утворюється сім’я характеристичних кривих, які залежать ще й від параметра x(s,t), y(s,t), u(s,t). Якщо із перших двох функцій можна визначити s і t через x і y,то ці криві утворять поверхню u(x,у). Достатньою умовою для цього є наступна умова

. (2.16)

З геометричної точки зору умова (2.16) означає, що тангенціальні та характеристичні напрями у кожній точці кривої повинні мати різні проекції на площині x,y. Якщо уздовж кривої ∆= , то для того щоб задача Коші мала розв'язки, крива повинна сама бути характеристикою. Якщо крива характеристика, то через неї, як початкову криву, проходить не одна, а нескінченна множина интегральних поверхонь, які перетинаються по кривій .

Теорема 2.5 Якщо праві частини системи звичайних диференціальних рівнянь

(2.17)

є неперервні функції своїх аргументів в області і, якщо крім того, в області існують неперервні частинні похідні , то існує єдиний розв’язок системи (2.9),(2.10) визначений початковими умовами , які знаходяться всередині області .

Теорема 2.6 Якщо на початковій кривій всюди ∆≠0. то задача Коші має один і тільки один розв'зок. Якщо ж уздовж кривої ∆=0, усюди, то для того щоб задача Коші мала розв'язок крива повинна бути характеристичною кривою.

У цьому випадку задача Коші має нескінченну множину розв'язків.

Для рівняння з двома незалежними змінними ставиться одна початкова умова, а якщо змінних більше, то .

Приклад 2.4

Знайти розв’язок задачі Коші

(2.18)

(2.19)

Розв’язок. Вибравши на кривій у якості параметра, отримаємо наступну задачу у просторі змінних

(2.20)

Характеристична система, що відповідає рівнянню (2.18), має вигляд

Отже, розв’язок характеристичної системи має вигляд

(2.21)

Інтегральна поверхня, що дає розв’язок задачі Коші (2.18),(2.19), утворена кусками характеристик для , що проходять через криву (2.21). Поклавши у рівняннях (2.21) та використавши (2.20), отримаємо

Підставляючи отримані значення в (2.21), отримаємо розв’язок задачі Коші (2.18), (2.19) у параметричній формі

(2.22)

Виключивши з (2.22) параметри та , отримаємо інтегральну поверхню у просторі

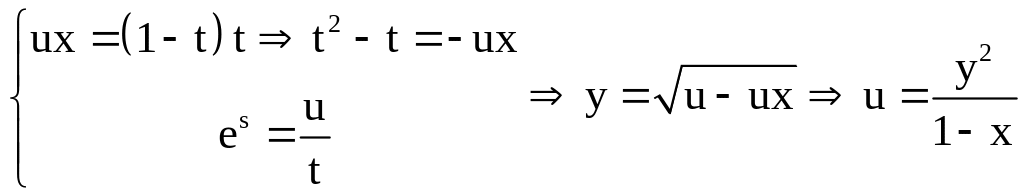Перевірка.

.

Приклад 2.5

Знайти загальний розв’язок рівняння та знайти функцію так, щоб вона пройшла через прямі .

(2.23)

Розв’язок.

Як і у попередньому прикладі складаємо систему звичайних диференціальних рівнянь

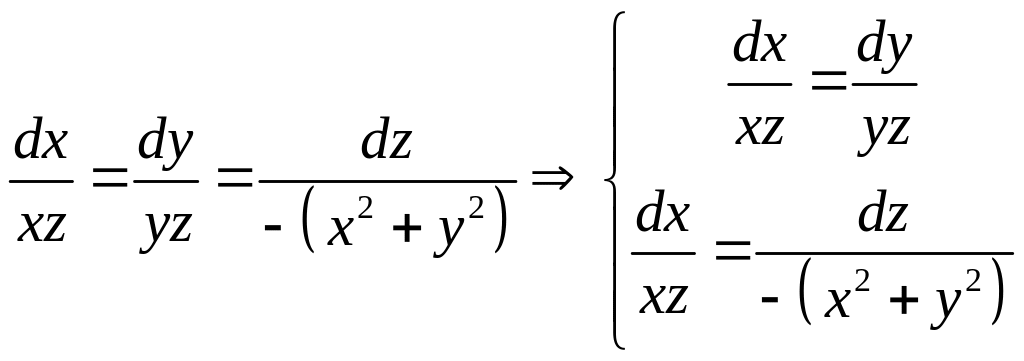
З першого рівняння системи .

Підставляємо отримане значення для у друге рівняння системи

.

Ми знайшли два лінійно незалежних інтеграли рівняння (2.23)

та (2.24)

Перше рівняння визначає сім’ю площин, що проходять через вісь , а друге – сім’ю сфер з центром у початку координат. Отже, інтегральними лініями рівняння (2.23) є сім’я кіл, що утворилася після перетину площин і сфер. Загальний розв’язок рівняння можна записати у вигляді

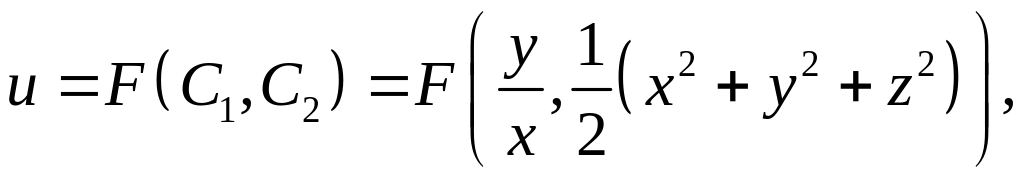де – довільна функція своїх аргументів.

Знайдемо функцію так, щоб вона пройшла через прямі .

Для цього виключимо з рівняння. З першого рівняння маємо: .

Підставивши отримані значення у друге рівняння співвідношення (2.24), одержимо

.

Підставляючи в останній вираз замість та значення (2.24), отримаємо частинний розв’язок

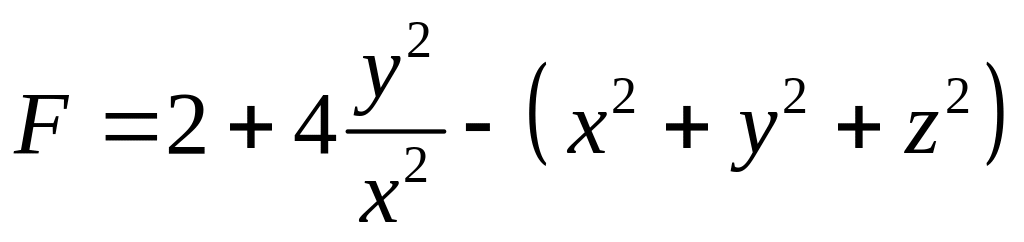
Перевірка. Знаходимо частинні похідні функції

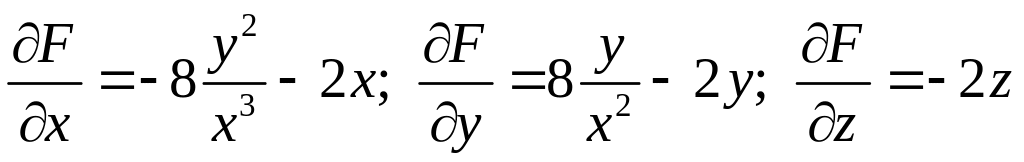
Підставивши отримані вирази у рівняння отримаємо тотожність.

У додатках часто зустрічаються задачі Коші для квазілінійного рівняння

(2.25)

(2.26)

де розглядається як час, а умова (2.26) – початкова функція на гіперплощині змінних . Рівнянню (2.25) відповідає характеристична система

(2.27)

Її необхідно розв’язувати з початковими умовами

(2.28)

З першого рівняння системи (2.27) та початкової умови знаходимо .

.