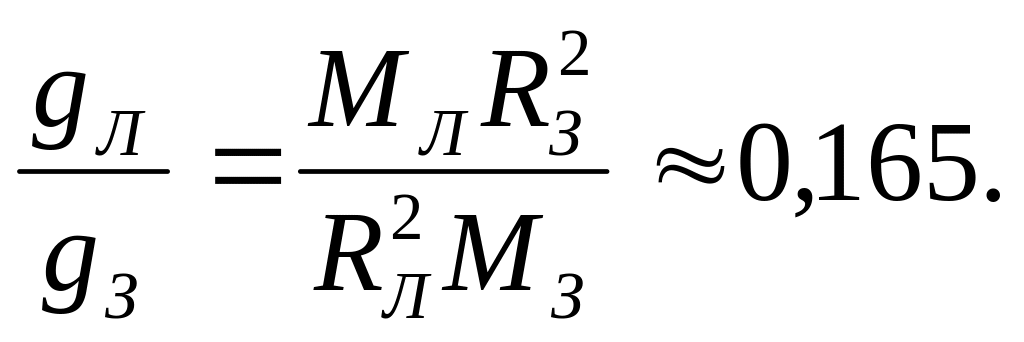1.4 Динамика вращательного движения

Основные законы и формулы

1. При криволинейном движении сила, действующая на материальную точку, может быть определена по формуле

где и – линейная и угловая скорости тела массой m; R – радиус кривизны траектории в данной точке.

Если касательная составляющая равнодействующей силы, действующей на точку, а нормальная составляющая с течением времени не меняется по величине, то точка будет равномерно двигаться по окружности

2. Между двумя точечными телами массами m₁ и m₂, находящимися на расстоянии r друг от друга, действует сила тяготения, которая определяется законом всемирного тяготения:

где γ – гравитационная постоянная: γ≈6,67∙10^-11 Н∙м²/кг².

3. Для характеристики вращательного движения твердых тел часто пользуются моментом М силы F относительно оси вращения.

Момент М является векторной величиной. Величина момента М некоторой силы F относительно оси вращения определяется формулой:

М=Fl,

где l – расстояние от оси вращения до прямой, вдоль которой действует сила.

4. Основное уравнение динамики вращательного движения:

а) в общем случае

М ω),

где М – момент силы, действующей на тело в течении времени dt, J – момент инерции тела, – угловая скорость, J – момент импульса;

б) в случае постоянных момента силы и момента инерции

в) в случае постоянного момента инерции

М=Jε,

где – угловое ускорение.

5. Момент импульса материальной точки

или

L=Jω,

где m – масса точки, – линейная скорость точки, r – расстояние точки от оси, относительно которой определяется момент импульса.

Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси z:

ω=const,

где J_z – момент инерции системы тел относительно оси z; – угловая скорость вращения тел системы вокруг оси z.

6. Момент инерции материальной точки:

где m – масса точки; r – расстояние до оси вращения.

Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:

а) стержня длиной l относительно оси, перпендикулярной стержню:

б) обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра):

где R – радиус обруча (цилиндра);

в) диска или сплошного цилиндра радиусом R относительно оси, перпендикулярной плоскости основания:

г) однородного шара радиуса R относительно оси, проходящей через его центр:

Теорема Штейнера:

где – момент инерции относительно оси, проходящей через центр масс; – момент инерции относительно параллельной оси, отстоящей от первой на расстоянии а; m – масса тела.

Общее условие равновесия тела гласит, что для того, чтобы тело находилось в равновесии, необходимо, чтобы были равны нулю равнодействующая приложенных к телу сил и сумма моментов этих сил относительно оси вращения:

F F_i = 0; M_i = 0.

Примеры решения задач

П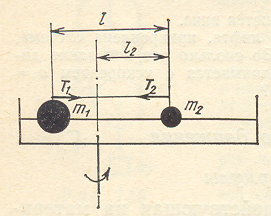 ример 1. Два шарика с массами m₁=40 г и m₂=10 г, надетые на горизонтальный стержень (рис. 7), связаны нитью длиной l=20 см. Определить силу натяжения нити при вращении стержня с угловой скоростью если шарики не смещаются относительно оси вращения. Трением шариков о стержень пренебречь. Рис.7

Решение. В данном случае нормальные ускорения шариков вызваны действием сил натяжения Т₁ и Т₂. Поскольку шарики не смещаются относительно оси вращения, то Т₁=Т₂. Согласно второму закону Ньютона, можно записать:

Тогда

поэтому

Сила натяжения нити будет равна:

П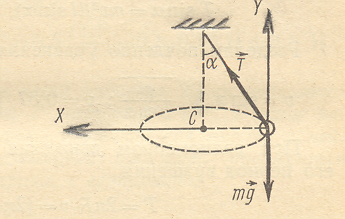 ример 2. Шарик массой 200 г, привязанный нитью к подвесу, описывает в горизонтальной плоскости окружность, имея постоянную скорость. Определить скорость шарика и период его вращения по окружности, если длина нити 1 м, а ее угол с вертикалью составляет 60⁰.

Решение. На шарик действуют: mg – сила тяжести, Т- сила натяжения нити (рис.8). Запишем для шарика уравнение второго закона Ньютона в векторной форме: Рис. 8

mg+Т = ma.

Спроецируем это уравнение на выбранные направления осей X и Y:

(1)

Учитывая, что (шарик не движется в вертикальном направлении,R – радиус окружности), , и подставляя выражение для а_х, а_у и R в (1), получаем:

(2)

Решив уравнения (2) получим:

При равномерном движении шарика по окружности его период вращения

П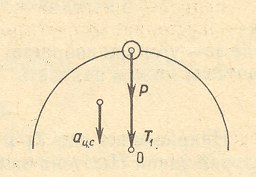 ример 3. Тело массой кг вращается на тонком стержне в вертикальной плоскости. Частота вращения равна , длина стержня см. Определить силу натяжения стержня: 1) в верхней и 2) в нижней точках.

Решение. 1. На тело в верхней точке действуют сила тяжести и Рис. 9

сила натяжения Т стержня (рис.9). В результате действия двух сил тело движется по окружности, т.е. с центростремительным ускорением

, (1)

где – угловая скорость; R – радиус траектории. Учитывая, что , можем записать

. (2)

Направление сил Т₁ и Р совпадает с вектором а_ц.с, поэтому второй закон Ньютона запишем в скалярном виде:

, (3)

или с учетом (2)

, (4)

откуда

. (5)

Выразим в СИ числовые значения R и g: R=0,125 м, g=9,81 м/с².

Вычислим по формуле (5) искомую силу натяжения стержня в верхней точке траектории:

.

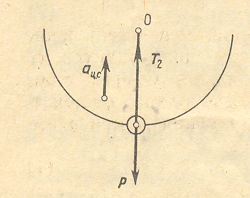
2. В нижней точке траектории на тело действуют (рис.10) те же силы и Т₂. Однако сила Р в данном случае направлена противоположно вектору а_ц.с. В связи с этим второй закон Ньютона имеет вид

Рис.10

,

откуда

.

После подстановки имеем

Пример 4. Маховик в виде диска массой m=50 кг и радиусом r=20 см, был раскручен до частоты n₁=480 об/мин и затем предоставлен самому себе. Под воздействием трения маховик остановился.

Найти момент М сил трения, считая его постоянным, принимая, что: а) маховик остановился через t=50 c; б) маховик до полной остановки сделал N=200 об.

Решение. а). По второму закону динамики вращательного движения изменение момента импульса вращающегося тела равно произведению момента силы, действующего на тело, на время действия этого момента

где J – момент инерции маховика, и – начальная и конечная угловые скорости, соответственно.

Так как то

Откуда

(1)

Момент инерции диска относительно его геометрической оси

Подставив выражение момента инерции в формулу (1), найдем:

(2)

Выразим угловую скорость маховика через частоту вращения

рад/с=50,2 рад/с.

Подставим числовые значения в формулу (2), получим

Н·м = –1 Н∙м.

б). В условии задачи дано число оборотов, сделанных маховиком до остановки, т.е. его угловое перемещение. Поэтому следует применить формулу, выражающую связь работы с изменением кинетической энергии:

или

(3)

так как

Работа при вращательном движении определяется по формуле:

Подставим это выражение работы, а также выражение момента инерции диска в формулу (3), получим:

Отсюда момент силы трения

(4)

Угол поворота в радианах

рад = 1256 рад.

Подставим числовые значения в выражение (4), найдем

Н·м = –1 Н∙м.

Знак «минус» показывает, что момент силы трения оказывает тормозящее действие.

Пример 5. Определить расстояние от центра Земли до искусственного спутника и скорость его относительно поверхности Земли, если спутник запущен так, что он движется в плоскости земного экватора и с Земли все время кажется неподвижным.

Решение. С достаточной степенью точности можно считать, что на спутник при его движении действует только сила земного притяжения:

где m – масса спутника; М – масса Земли; R – расстояние от центра Земли до спутника.

Под действием этой силы спутник, равномерно движется по окружности с ускорением поэтому где – скорость спутника. Учитывая, что можно записать:

Поскольку спутник с Земли все время кажется неподвижным, то где Т – период суточного вращения Земли ( Т=24 ч). Поэтому

откуда

.

Определим скорость движения спутника:

Пример 6. Сравнить ускорение свободного падения у поверхности Луны с ускорением свободного падения у поверхности Земли.

Решение. На тело массой m вблизи поверхности Земли и Луны будут действовать соответственно силы:

где – гравитационная постоянная; M_З и M_Л – массы соответственно Земли и Луны; R_З и R_Л – радиусы Земли и Луны. Эти силы будут сообщать телу соответствующие ускорения свободного падения:

поэтому

откуда