1.2 Кинематика криволинейного движения

Основные законы и формулы

1.Простейшим видом криволинейного движения является равномерное движение точки по окружности. При таком движении угловая скорость

где – угол поворота.

2.Полное ускорение точки при этом тангенциальное ускорение нормальное (центростремительное) ускорение

3.В случае равномерного вращательного движения угловая скорость может быть выражена формулой:

где Т – период вращения; – частота вращения.

4.Угловая скорость связана с линейной скоростью соотношением:

.

5.Для характеристики переменного вращательного движения вводят угловое ускорение :

При равнопеременном вращательном движении ( ) будем иметь:

Тангенциальное и нормальное ускорения могут быть выражены через угловую скорость и ускорение следующим образом:

Примеры решения задач

Пример 1. Сравнить линейные скорости и центростремительные ускорения точек земной поверхности на экваторе и на широте . Радиус Земли R принять равным 6400 км.

Решение. Линейная скорость любой точки на экваторе

где Т=24 ч=86400 с – период суточного вращения Земли.

Центростремительное ускорение определяется следующим образом:

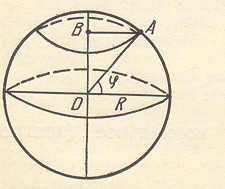
На широте (рис. 1) будем иметь:

Рис. 1

Чтобы сравнить величины линейных скоростей и центростремительных ускорений, необходимо найти следующие отношения:

Пример 2. Колесо вращается с постоянным угловым ускорением Через 0,5 с после начала движения полное ускорение колеса см/с². Чему равен радиус колеса?

Решение. Полное ускорение

.

Используя формулы связи линейных и угловых характеристик, можно записать:

Тогда

Угловую скорость определим так:

но , поэтому Следовательно,

откуда

Пример 3. Автомобиль движется по закруглению шоссе, имеющему радиус кривизны R= 50 м. Уравнение движения автомобиля s= A+Bt+Ct², где А=10 м, В=10 м/с, м/с². Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорение в момент времени t=5c.

Решение. Прежде всего находим общее выражение для скорости автомобиля. Известно, что

Взяв производную по времени от заданного уравнения пути s, получим:

Подставив сюда значения постоянных В и С, а также заданное значение времени, найдем скорость:

Теперь находим общее выражение для тангенциального ускорения. Из теории известно, что

Взяв производную по времени от общего уравнения скорости и подставив значения постоянной С и времени, получим

Полученное выражение для тангенциального ускорения не содержит времени; это значит, что тангенциальное ускорение постоянно по величине, поэтому движение автомобиля является равнозамедленным.

Значение нормального ускорения найдем, подствив в общее уравнение его известные значения скорости и радиуса кривизны траектории:

м/с².

Полное ускорение будет равно геометрической сумме взаимно препендикулярных тангенциального и нормального ускорений:

м/с².

Направление полного ускорения можно определить, если найти угол, образуемый полным ускорением с направлением нормального ускорения:

Пример 4. Вал начинает вращаться и в первые 10 с совершает 50 оборотов. Считая вращение вала равноускоренным, определить угловое ускорение и конечную угловую скорость.

Решение. Поскольку начальная угловая скорость равна нулю, уравнение движения и формула угловой скорости примут вид:

; .

Так как угловое перемещение, соответствующее одному полному обороту вала, равно , то полное угловое пермещение, соответствующее N оборотам, . Подставив это выражение в уравнение движения, получим , откуда

; рад/с².

Зная значение , вычислим конечную угловую скорость вращения:

; =62,8 рад/с.