3.Применение методов аналитиЧеской Механики к анализу движениЯ механиЧеских систем
Основу аналитической механики составляют общие принципы, из которых аналитическим путем могут быть получены основные дифференциальные уравнения движения или условия равновесия механической системы.
В данном разделе курсовой работы требуется:
составить дифференциальные уравнения движения системы (желательно несколькими способами);
найти решения дифференциальных уравнений движения (в большинстве случаев численными методами);
построить графики изменения координат и скоростей на заданном интервале времени;
произвести анализ движения системы, варьируя начальные условия и параметры системы;
решить другие задачи, которые могут быть поставлены преподавателем индивидуально.
3.1. Связи и виртуальные перемещения
Пусть
имеется система, состоящая из N
материальных точек
Если на положения и скорости точек
наложены ограничения геометрического
или кинематического характера (
механические связи ), то такая система
называется несвободной. Для свободных
систем связи отсутствуют.
Если
скорости точек
не входят в уравнения связей, то такие
связи называются конечными или
геометрическими. Ограничения, накладываемые
на движение системы такой связью, могут
быть описаны уравнением
,
(3.1)
где
- радиусы-векторы точек
,
t - время.
Связь, описываемая уравнением
, (3.2)
называется кинематической. Если она путем интегрирования не может быть приведена к виду (3.1), то ее называют неголономной или дифференциальной.
Связь называется стационарной, если время явно не входит в уравнение связи
(3.3)
и нестационарной, если параметр t присутствует, например, (3.1).
Система называется склерономной, если на нее наложены только стационарные связи. В противном случае система называется реономной.
Связи, которые записываются в виде равенства (например, (3.1)), называются удерживающими, а которые в виде неравенства - неудерживающими
.
Пусть на материальную систему наложены d конечных связей
(3.4)
и g линейных дифференциальных связей
, (3.5)
где
-
вектор и скаляр, представляющие собой
заданные функции отt
и
.
Продифференцируем уравнения конечных связей (3.4)
(3.6)
Систему
векторов
будем называть возможными скоростями
для некоторого времениt
и для некоторого возможного в этот
момент положения системы, если векторы
удовлетворяютd+g
линейным уравнениям (3.5) и (3.6).
Для каждого возможного положения системы в момент времени t существует бесчисленное множество систем возможных скоростей.
Систему
бесконечно малых перемещений
будем называть возможными перемещениями.
Умножив уравнения (3.5) и (3.6) на dt, получим уравнения, определяющие возможные перемещения
(3.7)
Возьмем две системы возможных перемещений для одного и того же момента времени и для одного и того же положения системы:
и
.
Как
,
так и
,
удовлетворяют системе (3.7), а их разности
(3.8)
удовлетворяют соотношениям:
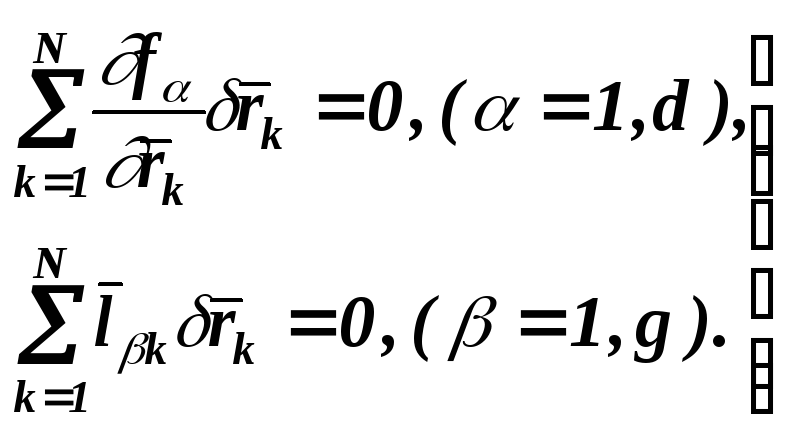(3.9)
Векторы
,
удовлетворяющие соотношениям (3.9)
называются виртуальными перемещениями.
Сравнивая выражения (3.7) и (3.9) можно
заключить, что виртуальные перемещения
совпадают с возможными перемещениями
при “замороженных” связях.
Можно еще сказать, что виртуальные перемещения представляют собой перемещения точек системы из одного возможного положения системы в момент времени t в другое бесконечно близкое, возможное для того же самого момента времени t, положение системы.
При стационарных связях виртуальные перемещения совпадают с возможными.