Яблонский К1, К2 вариант 20

I. Кинематика точки

Задание К.1. Определение скорости и ускорения точки по заданным уравнениям ее движения

По заданным уравнениям движения точки М установить вид её траекто-рии и для момента времени t=t₁ (с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Исходные данные:

х = 2 – 3t – 6t²; y = 3 – 3t/2 – 3t²;

t₁ = 0 (x и y – в см, t и t₁ – в с).

Решение. Чтобы получить уравнения траектории в координатной форме, исключим время t из уравнений.

х = 2 – 3t – 6t²

х – 2 = – 3∙(t + 2t²)

t + 2t² = (х – 2)/(– 3)

y = 3 – 3t/2 – 3t² = (6 – 3t – 6t²)/2 = (6 – 3∙(t + 2t²))/2

(2y – 6)/(– 3) = (х – 2)/(– 3)

2y = х + 4

y = (х + 4)/2, т.е. траекторией точки является прямая.

Вектор скорости точки

Вектор ускорения точки

Найдем их, дифференцируя по времени уравнения движения:

По найденным проекциям определяем модуль скорости:

;

и модуль ускорения точки:

;

Модуль касательного ускорения точки

Модуль нормального ускорения точки

Определим радиус кривизны траектории точки М в момент времени t₁=0.

Результаты вычислений заносим в таблицу

Координа-ты, см		Скорость, см/с			Ускорение, см/с2					Радиус кри-визны, см
x	y	vX	vY	v	aX	aY	a	aτ	an	ρ
2	3	-3	-1,5	3,35	-12	-6	13,4	13,4	0	∞

Найдем положение точки М в заданный момент времени t₁ = 0.

х = 2 – 3t – 6t² = 2

y = 3 – 3t/2 – 3t²= 3

x	-10	-7	-4	-1	2
y	-3	-1,5	0	1,5	3

Вектор строим по составляющим и . Вектор строим по составляю-щим изатем раскладываем на составляющие и .

II. Кинематика твердого тела

Задание К.2. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях

Движение груза должно описываться уравнением

где t – время, с; с₀, с₁, с₂ – некоторые постоянные.

В начальный момент времени (t = 0) положение груза определяется коор-динатой х₀, и он имеет скорость v₀. Учесть, что в момент времени t = t₂ ско-рость и ускорение груза и точки М одного из колес механизма.

Определить коэффициенты с₀, с₁ и с₂, при которых осуществляется тре-буемое движение груза 1. Определить также в момент времени t = t₁ скорость и ускорение груза и точки М одного из колес механизма.

Дано:R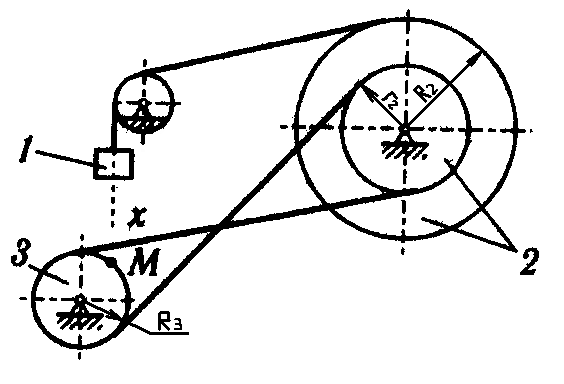₂ = 25 см

r₂ = 15 см

R₃ = 10 см

x₀ = 10 см

v₀ = 8 см / с

x₂ = 277 см

t₂ = 3 с

t₁ = 1 с

Решение.

Уравнение движения груза 1 имеет вид:

(1)

Коэффициенты с₀, с₁ и с₂ могут быть определены из следующих условий:

при (2)

при (3)

Скорость груза 1:

(4)

Подставляя (2) и (3) в формулы (1) и (4), находим коэффициенты:

277 = С₂∙9 + 8∙3 + 10

С₂ = 27 см / с²

Таким образом, уравнение движения груза 1:

(5)

Скорость груза 1:

(6)

Ускорение груза 1:

Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза v и угловые скорости колёс и .

В соответствии со схемой механизма

(7)

откуда

Угловое ускорение колеса 3:

Скорость точки М, её вращательное, центростремительное и полное ускорения определяются по формулам:

Результаты вычислений для заданного момента времени t₁ = 1 с приведе-ны в таблице.

62	54	3,7	3,24	37,2	138,4	32,4	142

С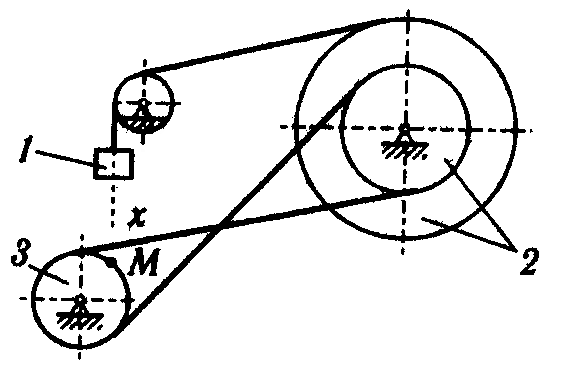корости и ускорения тела 1

и точки М показаны на рисунке.