Яблонский К1 вариант 12

К-1. Определение скорости и ускорения точки по заданным уравнениям ее движения.

По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t₁ (c) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Исходные данные: x = 5sin²(πt/6); y = – 5cos²(πt/6) – 3; t₁ = 1 (x и y — в см, t и t₁ — в с).

Решение.

Определение траектории движения точки М.

Уравнения движения точки можно рассматривать как параметрические, поэтому перейдем к их координатной форме, используя формулу sin²α + cos²α = 1.

sin²(πt/6) = x/5; cos²(πt/6) = –(y+3)/5; (1)

x – y – 3 = 5;

y = x – 8 (прямая, рис К1.1)

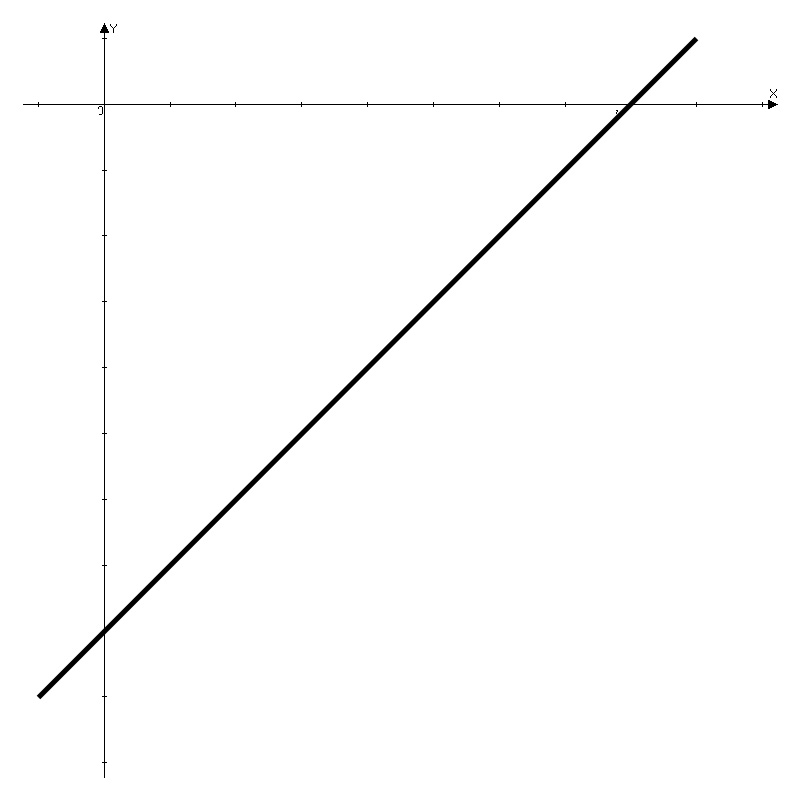
рис. К1.1

Определение положения точки М в момент времени t₁ =1с.

Подставляя значения t₁ =1с в формулы (1), надем координаты точки в данный момент времени:

x₁ = 1,25 см, y₁ = – 6,75 см

Определение скорости точки М в момент времени t₁ =1с.

При t₁ = 1c:

Определение полного, касательного и нормального ускорения точки М в момент времени t₁ =1с.

При t₁ = 1c:

Полное ускорение:

Касательное ускорение:

Нормальное ускорение:

Определение радиуса кривизны:

Результаты всех расчетов занесены в табл. К1.1

Таблица К1.1

Координаты		Скорость, см/с			Ускорение, см/с2					Радиус кривизны, см
x	y	vx	vy	v	ax	ay	a	aτ	an	ρ
1,25	-6,75	2,267	2,267	3,206	1,3707	1,3707	1,938	1,938	0	∞

4