

Министерство образования и науки рф
филиал
Государственного образовательного учреждения
высшего профессионального образования-
Всероссийского заочного финансово-экономического института
в г.
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ
по дисциплине «Экономико-математические методы и прикладные модели»
на тему: «Вариант 10»
Выполнил:
Проверил:
2010 г.
Содержание:
Задача №1…………………………………………………………..стр.3
Задача №2…………………………………………………………..стр.8
Список литературы………………………………………………..стр.14
Задача №1
Фирма собирается разрабатывать пять новых программных продуктов. Потребности проектов, денежные ресурсы фирмы в каждом из кварталов и ожидаемая прибыль от реализации программных продуктов представлены в таблице. Разработку каких программных продуктов следует финансировать, чтобы получить наибольшую прибыль?
Период |
Программные продукты |
Ресурсы фирмы
|
||||
A |
B |
C |
D |
E |
||
I кв |
4 |
7 |
11 |
2 |
12 |
34 |
II кв |
5 |
9 |
8 |
6 |
7 |
30 |
III кв |
2 |
9 |
– |
9 |
3 |
27 |
IV кв |
2 |
4 |
– |
9 |
– |
39 |
Прибыль |
12 |
21 |
10 |
18 |
19 |
|
Экономико-математическая модель
Обозначим через Х1, Х2, Х3, Х4, Х5 объемы разработки соответствующего вида продукции (количество программной продукции каждого вида).
Целевая функция – это математическая запись критерия оптимальности, т.е. выражение, которое необходимо максимизировать.
f(![]() )
= 12х1
+ 21х2 +
10х3
+ 18х4
+ 19х5
→ max
)
= 12х1
+ 21х2 +
10х3
+ 18х4
+ 19х5
→ max
Ограничения по ресурсам:
![]()
Решение:
Приведенная ЭММ является моделью задачи линейного программирования (ЗЛП). Она может быть реализована симплекс-методом. Получим решение средствами пакета Excel.
1. Создадим форму для ввода условий задачи. Запустим Excel, выбрав Microsoft Excel из Программы главного меню Windows. Открывается чистый лист Excel. Создаём текстовую форму – таблицу для ввода условий задачи.
Вводим исходные данные в созданную форму-таблицу (Рис.1).

Рис. 1
2. Вводим зависимость для целевой функции:
Курсор в ячейку G4.
Курсор на кнопку «Мастер функций», расположенную на панели инструментов.
Курсор в окно «Категория» на категорию Математические.
Курсор в окно Функция на СУММПРОИЗВ.
На экране появляется диалоговое окно СУММПРОИЗВ.
В строку «Массив 1» ввести; $B$3:$F$3.
В строку «Массив 2» ввести B4:F4.
Кнопка «ОК». На экране: в ячейку G4 введена функция.
3. Вводим зависимости для ограничений:
Курсор в ячейку G4.
На панели инструментов кнопка Копировать в буфер.
Курсор в ячейку G7.
На панели инструментов кнопка Вставить из буфера.
Курсор в ячейку G8.
На панели инструментов кнопка Вставить из буфера.
Курсор в ячейку G9.
На панели инструментов кнопка Вставить из буфера.
Курсор в ячейку G10.
На панели инструментов кнопка Вставить из буфера.
4. В строке Меню указатель мыши на имя Сервис. В развернутом меню команда Поиск решения. Появляется диалоговое окно Поиск решения.
5. Назначить целевую функцию (установить целевую ячейку):
Курсор в строку Установить целевую ячейку.
Вводим адрес ячейки $G$4.
Вводим направление целевой функции в зависимости от условия нашей задачи – Максимальному значению.
Курсор в строку Изменяя ячейки.
Водим адреса искомых переменных B$3:F$3.
6. Вводим ограничения:
Указатель мыши на кнопку Добавить. Появится диалоговое окно Добавление ограничения.
В строке Ссылка на ячейку вводим адрес $G$7.
Вводим знак ограничения ≤.
В строке Ограничение вводим адрес $I$7.
Указатель мыши на кнопку Добавить. Появится диалоговое окно Добавление ограничения.
В строке Ссылка на ячейку вводим адрес $G$8.
Вводим знак ограничения ≤.
В строке Ограничение вводим адрес $I$8.
Указатель мыши на кнопку Добавить. Появится диалоговое окно Добавление ограничения.
В строке Ссылка на ячейку вводим адрес $G$9.
Вводим знак ограничения ≤.
В строке Ограничение вводим адрес $I$9.
Указатель мыши на кнопку Добавить. Появится диалоговое окно Добавление ограничения.
В строке Ссылка на ячейку вводим адрес $G$10.
Вводим знак ограничения ≤.
В строке Ограничение вводим адрес $I$10.
Указатель мыши на кнопку ОК.
На экране появится диалоговое окно Поиск решения с введенными условиями (Рис.2).
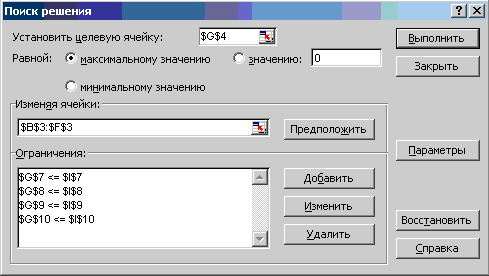
Рис.2
7. Вводим параметры для решения ЗЛП:
В диалоговом окне указатель мыши на кнопку Параметры. На экране появляется диалоговое окно Параметры поиска решения.
Устанавливаем флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения.
Указатель мыши на кнопку ОК. На экране диалоговое окно Поиск решения.
Указатель мыши на кнопку Выполнить.
Через непродолжительное время появляется диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками В3:F3 для значений Хi и ячейка G4 с максимальным значением целевой функции.
8. Сохранить найденное решение.
9. Укажем тип отчета Результаты, получим дополнительную информацию об оптимальном решении.
Вывод: Полученное решение означает, что максимальную прибыль 85,2 ден.ед. фирма может получить при финансировании программных продуктов D и F.
