
Контрольные задания
Задание I. По координатам вершин пирамиды А1А2А3А4 найти: 1) длины ребер А1А2 и А1А3; 2) угол между ребрами А1А2 и А1А3; 3) площадь грани А1А2А3; 4)объем пирамиды; 5) уравнения прямых А1А2 и А1А3; 6) уравнения плоскостей А1А2А3 и А1А2А4; 7) угол между плоскостями А1А2А3 и А1А2А4.
1. А1(-1; 2; 1), А2(-2; 2; 5), А3(-3; 3; 1), А4(-1; 4; 3).
2. А1(-1; 1; -1), А2(-3; 1; 3), А3(-4; 2; -1), А4(-2; 3; 1).
3. А1(1; 1; 2), А2(0; 1; 6), А3(-1; 2; 2), А4(1; 3; 4).
4. А1(-1; -2; 1), А2(-2; -2; 5), А3(-3; -1; 1), А4(-1; 0; 3).
5. А1(2; -1; 1), А2(1; -1; 5), А3(0; 0; 1), А4(2; 1; 3).
6. А1(-1; 1; -2), А2(-2; 1; 2), А3(-3; 2; -2), А4(-1; 3; 0).
7. А1(1; 2; 1), А2(0; 2; 5), А3(-1; 3; 1), А4(1; 4; 3).
8. А1(-2; -1; 1), А2(-3; -1; 5), А3(-4; 0; 1), А4(-2; 1; 3).
9. А1(1; -1; 2), А2(0; -1; 6), А3(-1; 0; 2), А4(1; 1; 4).
10. А1(1; -2; 1), А2(0; -2; 5), А3(-1; -1; 1), А4(1; 0; 3).
Задание II. Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисления. Проверить правильность вычисления обратной матрицы, используя матричное умножение.
11.
![]() 12.
12.
![]() 13.
13.
![]()
14.
![]() 15.
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]() 19.
19.
![]()
20.
![]()
Задание III. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.
21. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
 ;
;
4)
![]() .
.
22. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() .
.
23. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() .
.
24. 1)
![]() ;
2)
;
2)
 ;
3)
;
3)
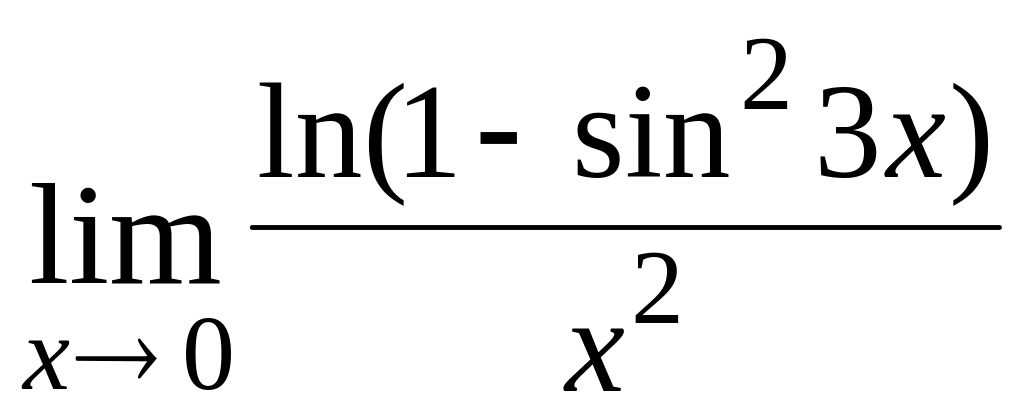 ;
;
4)
![]() .
.
25. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
 ;
;
4)
![]() .
.
26. 1)
![]() ;
2)
;
2)
 ;
3)
;
3)
![]() ;
;
4)
![]() .
.
27. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() .
.
28. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() .
.
29. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() .
.
30. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() .
.
Задание IV. Найти алгебраическую и тригонометрическую формы числа
z = z1+z2. Изобразить числа z1, z2, z3 на комплексной плоскости. Вычислить z12 по формуле Муавра.
Номер задачи |
z1 |
z2 |
Номер задачи |
z1 |
z2 |
31. |
-2 |
|
32. |
-2i |
|
33. |
-2 |
|
34. |
-2i |
|
35. |
2 |
|
36. |
-2i |
|
37. |
2 |
|
38. |
2i |
|
39. |
2 |
|
40. |
-2 |
|
Задание V. Найти производные первого порядка, используя правила вычисления производных.
41. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]() .
.
42. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]() .
.
43. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]()
44. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]()
45. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]()
46. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]()
47. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]()
48. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]()
49. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]()
50. 1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]()
Задание VI. Построить график функции у=f(х), используя общую схему исследования функции.
51. у=х3+6х2+9х+4 52. у=х3+3х2-9х+5 53. у=х3+6х2-15х+8
54. у=х3-3х2-24х-28 55. у=х3+12х2+45х+50 56. у=х3-6х2+9х-4
57. у=х3-3х2-9х-5 58. у=х3-6х2-15х-8 59. у=х3+3х2-24х+28
60. у=х3-12х2+45х-50
Задание VII. Найти частные производные первого порядка:
61. z=cos(х3y)+х2+y 62. z=arcsin(4хy)+х2y 63. z=tg(3х3-2)+8y
64. z=3xy-4y 65. z=5х3+2yх2+e2xy 66. z=cos(х3-6)+9х-4
67. z=ln(3хy5)-yх2-25 68. z=ctg(х+4y2)-4хy-8 69. z=arctg(х-y)+хy-8
70. z=e2x-y sin(3y)
Таблица вариантов
-
Вариант
Номера заданий
1
2
3
4
5
6
7
8
9
10
1 11 21 31 41 51 61
2 12 22 32 42 52 62
3 13 23 33 43 53 63
4 14 24 34 44 54 64
5 15 25 35 45 55 65
6 16 26 36 46 56 66
7 17 27 37 47 57 67
8 18 28 38 48 58 68
9 19 29 39 49 59 69
10 20 30 40 50 60 70
Л и т е р а т у р а
Письменный Д.Т. Конспект лекций по высшей математике: полный курс / Д.Т.Письменный. – М.: Айрис-пресс, 2007. – 608 с.
Пискунов Н.С. Дифференциальное и интегральное исчисления: Учеб. для втузов. В 2-х т. Т. I / Н.С.Пискунов. – М.: Интеграл-пресс, 2002. – 251 с.
Пискунов Н.С. Дифференциальное и интегральное исчисления: Учеб. для втузов. В 2-х т. Т. II / Н.С.Пискунов. – М.: Интеграл-пресс, 2002. – 544 с.
Гусак А.А. Высшая математика. В 2-х т. Т. I / А.А.Гусак. – Мн.: ТетраСистемс, 2001. – 443 с.
Гусак А.А. Высшая математика. В 2-х т. Т. II / А.А.Гусак. – Мн.: ТетраСистемс, 2001. – 447 с.
Шипачев В.С. Задачник по высшей математике: Учеб. пособие для вузов / В.С.Шипачев. – М.: Высш. шк., 1998. – 304 с.
Данко П.Е. Высшая математика в упражнениях и задачах. В 2-х т. Т. I / П.Е.Данко, А.Г.Попов, П.Я.Кожевникова. – М.: Высшая школа, 1986. – 303 c.
Зимина О.В. Высшая математика / О.В.Зимина, А.И.Кириллов, Т.А.Сальникова; под редакцией А.И.Кириллова. – 3-е изд., испр. – М.: ФИЗМАТЛИТ, 2005. – 368 с.
