Шпора по термеху5

1-ПРЕДМЕТ Теоретическая механика - это наука о равновесии тел в пространстве, о системах сил, и о переходе одной системы в другую.

2. Сопротивление материалов - наука о расчетах конструкций на прочность, жесткость и устойчивость.

3. Детали машин - это курс, изучающий назначение, классификацию и основы расчета деталей общего типа.

Механические движения - это изменение положения тела в пространстве и во времени. Материальная точка - это тело, формами и размерами которого можно пренебречь, но которое обладает массой.

Абсолютно твердое тело - это тело, у которого расстояние между любыми двумя точками остается неизменным при любых условиях.

Сила - мера взаимодействия тел.

Сила - векторная величина, которая характеризуется:

1. точкой приложения;

2. величиной (модулем);

3. направлением.

2-СИЛА ЕЕ ХАРАКТЕРИСТИКИ-Сила - векторная величина, которая характеризуется:

1. точкой приложения;

2. величиной (модулем);

3. направлением.

3-АКСИОМЫ СТАТИКИ-

1. Изолированная точка - это материальная точка, которая под действием сил движется равномерно прямолинейно, либо находится в состоянии относительного покоя.

2. две силы равны, если они приложены к одному телу, действуют вдоль одной прямой и направлены в противоположные стороны, такие силы называются уравновешивающими.

3. Не нарушая состояния тела к нему можно приложить или от него отбросить уравновешивающую систему сил.

Следствие: всякую силу можно переносить вдоль линии её действия, не изменяя действия силы на данное тело.

4. Равнодействующая двух сил приложенных в одной точке, приложена в той же точке и является по величине и направлению диагональю параллелограмма, построенных на данных силах.

5. Всякому действию есть равное по величине и направлению противодействие.

4-СВЯЗИ РЕАКЦИИ СВЯЗЕЙ-Свободное тело - это такое тело, перемещение которого в пространстве ничего не меняет.

Те тела, которые ограничивают перемещение выбранного тела называются связями.

Силы, с которыми связь удерживают тело называются реакциями связей.

При решении задач мысленно связи отбрасываются и заменяются реакциями связей.

1. Связь в виде гладкой поверхности

2. Гибкая связь.

3. Связь в виде жесткого стержня.

4. Опора в точке или опора углу.

5. Шарнирно подвижная опора.

6. Шарнирно неподвижная опора.

5-СИСТЕМА СХОДЯЩИХСЯ СИЛ-Система сил - это совокупность.

Система сил

Плоская Пространственная

Сходящиеся Параллельные Сходящиеся Параллельные Плоская система сходящихся сил - это система сил линии действия, которых сходятся в одной точке называются сходящимися.

Пусть дана система сходящихся сил F1, F2, F3, линии, действия которых сходятся в точке О. для того, чтобы заменить эту систему сил равнодействующей силой необходимо:

1. Перенести силы в точку О (на основании следствия из аксиом).

2. Почленно сложить вектора сил (на основании аксиомы 4). Равнодействующая всегда направлена из начала первого вектора в конец последней. В результате векторного сложения образуется силовой многоугольник.

Плоская система сходящихся сил имеет два условия равновесия: 1. Геометрическое условие: плоская система сходящихся сил находится в равновесии, если силовой многоугольник замкнут, т. е. равнодействующая равна нулю. 2. Аналитическое условие: плоская система сходящихся сил находится в равновесии если алгебраические суммы проекций всех сил системы на оси х и у равны нулю. ?Fix = 0 ?Fiy = 0

9-Пара сил - это система двух равных сил, лежащих на параллельных прямых и направленных в противоположные стороны.

Действие пары на тело определяется моментом на пару.

Момент - это произведение модуля силы на плечо.

Плечо - кратчайшее расстояние между линиями действия силы.

Если пара поворачивает плечо по ходу часовой стрелки, то момент считается положительным, а если против хода, то отрицательным.

Пара сил обладает свойствами:

1. не нарушая действия пары на тело можно её переносить в любую точку плоскости.

2. Две пары сил являются эквивалентными, если их моменты равны.

Система пар сил находится в равновесии, если сумма моментов всех пар системы равно нулю.

?Mi(F) = 0

10-Момент силы относительно точкиЕсли имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки O и O_F, на вектор силы :

.Момент силы относительно осиМоментом силы относительно оси называется момент проекции силы на плоскость перпендикулярную оси относительно точки пересечения оси с этой плоскостью

12-система сил - это совокупность.

Система сил

Плоская Пространственная

Сходящиеся Параллельные Сходящиеся Параллельные

13-Теорема Вариньона — одна из теорем механики, устанавливающая зависимость между моментами сил данной системы и моментом их равнодействующей силы относительно какого-либо центра или оси. Сформулирована для сходящихся сил Пьером Вариньоном (Varignon) в 1687.

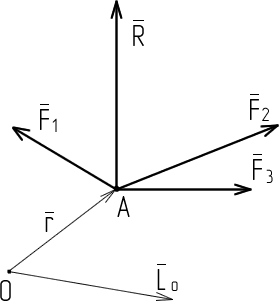
Теорема Вариньона гласит: момент равнодействующей силы относительно какой-либо точки (центра) равен сумме моментов сил, составляющих эту равнодействующую относительно той же точки (центра).

Векторная запись теоремы: .

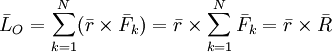15-трения и качения-Рассмотрим цилиндр, покоящийся на горизонтальной плоскости, когда на него действует горизонтальная сила Q; кроме неё действуют сила тяжести P, а также нормальная реакция N и горизонтальная реакция плоскости (сила сцепления с плоскостью) F_c. Заметим, гладкая плоскость не имеет силы F_c, а N имеется всегда при наличии контакта.

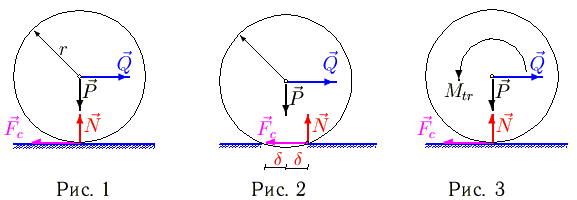
Как показывает опыт, при достаточно малом модуле силы Q цилиндр остаётся в покое. Но этот факт нельзя объяснить, если удовлетвориться введением сил, изображенных на рис.  1. Согласно этой схеме равновесие невозможно, так как главный момент всех сил, действующих на цилиндр Qr, отличен от нуля. Для устранения отмеченного несоответствия с опытом необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности цилиндр и плоскость вблизи точки контакта деформируется и существует некоторая площадка контакта конечной ширины 2. Если под действием внешних сил цилиндр будет катится направо, то реакция опоры будет также смещена направо. Цилиндр будет катиться направо, поворачиваясь в каждый момент вокруг некоторой точки плоскости, к которой приложены реакции N и F_c (рис. 2 ). Считая деформацию малой, заменим эту систему сил системой, изображенной на рис.  3. К цилиндру приложена пара сил с моментом M_tr=N. Этот момент называется моментом силы трения качения. Коэффициент трения  качения имеет размерность длины.

18-Центр параллельных сил - базис параллельных сил, точка, через которую проходит линия действия равнодействующей системы параллельных сил Fk при любом повороте всех сих сил около их точек приложения в одно и ту же сторону и на один и тот же угол. Координаты Ц. п. с. определяются формулами: , , где xk, yk, zk - месторасположение точек приложения сил. Понятием Ц. п. с. пользуются при отыскании координат центров тяжести тел.

59-Общие сведения о червячных передачах. Черв передача относятся к передачи зацепления с перекрещивающими осями. Состоит из червяка и червячного колеса. Достоинства: а) возможность получения большого передаточного отношения в одной ступице б) плавность и бесшумность работы в) возможность выполнения самотормозящейся пары г)компактность и сравнительно небольшая масса. Недостатки: а) низкий КПД от 0,7 до 0,85, а в самотормозящихся парах до 0,5 б) необходимость применения для венца колеса дорогостоящих антифр материалов в) значительное тепловыделение. Ч.п. классифицируется: По форме поверхности червяка: цилиндрические, глобоидные По форме профиля витка резьбы: с прямолинейным профилем, с криволинейным профилям

19-КИНЕМАТИКА-В кинематике рассматриваются различные виды движения тел без учета влияния сил, действующих на эти тела. При поступательном движении тела все точки тела движутся одинаково, и, вместо того чтобы рассматривать движение каждой точки тела, можно рассматривать движение только одной его точки. Основные характеристики движения материальной точки: траектория движения, перемещение точки, пройденный ею путь, координаты, скорость и ускорение. Линию, по которой движется материальная точка в пространстве, называют траекторией. Перемещением материальной точки за некоторый промежуток времени называется вектор перемещения ∆r=r-r₀, направленный от положения точки в начальный момент времени к ее положению в конечный момент. Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета. Скорость - это производная радиуса - вектора по времени.

либо, применяя другое обозначение производной по времени,

Ускорение - вторая производная радиуса-вектора по времени. Производную по времени от какой-либо величины называют скоростью изменения этой величины. Ускорение - это скорость изменения скорости. Нормальное ускорение направлено по нормали к скорости, его модуль:

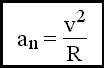
Вектор ускорения характеризует быстроту и направление изменения скорости материальной точки относительно тела отсчета.

20-ЗАКОН ДВИЖЕНИЯРавномерное прямолинейное движение

Равномерным прямолинейным движением называется такое прямолинейное движение, при котором материальная точка (тело) движется по прямой и в любые равные промежутки времени совершает одинаковые перемещения.

Вектор скорости равномерного прямолинейного движения материальной точки направлен вдоль ее траектории в сторону движения. Вектор скорости при равномерном прямолинейном движении равен вектору перемещения за любой промежуток времени, поделенному на этот промежуток времени:

Примем линию, по которой движется материальная точка, за ось координат ОХ, причем за положительное направление оси выберем направление движения точки. Тогда, спроецировав векторы r и v, на эту ось, для проекций ∆r_x = |∆r|   и   ∆v_x = |∆v| этих векторов мы можем записать:

, отсюда получаем уравнение равномерного движения:

∆r_x = v_x · t .

Т.к. при равномерном прямолинейном движении S = |∆r|, можем записать: S_x = v_x · t. Тогда для координаты тела в любой момент времени имеем:

х = х₀ + S_x = х₀ + v_x · t,

где х₀ - координата тела в начальный момент t = 0.

-

21-виды движения точки-Имеется пять видов движения твердого тела:

     1)поступательное, если прямая, соединяющая любые две точки тела, перемещается, оставаясь параллельной своему начальному положению, например движение трамвая на прямом участке пути;

     2) вращательное, если все точки лежащие на некоторой прямой, называемой осью вращения, остаются неподвижными, например движение двери при открывании и закрывании;

     3) плоское, если все точки тела движутся в плоскостях, параллельных некоторой плоскости, неподвижной в рассматриваемой системе отсчета, например качение колеса на прямом участке пути;

      4)сферическое, если одна из точек тела остается все время неподвижной в рассматриваемой системе отсчета, например движение гироскопа с тремя степенями свободы в карданном подвесе;

      5)свободное, если нет перечисленных выше четырех ограничений, например движение свободного произвольного брошенного тела вблизи поверхности Земли.

     Первые два движения являются основными движениями твердого тела. Остальные виды движения твердого тела можно свести к одному из основных движений или к их совокупностиПри поступательном движении все точки твердого тела совершают равные перемещения за один и тот же промежуток времени. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Этот факт позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной частицы тела

22- Вращательным движением называется движение, при котором все точки тела описывают окружности. Центры этих окружностей лежат на прямой, называемой осью вращения. В общем случае движение твердого тела можно представить как результат сложения поступательного и вращательного движений. При вращательном движении все точки тела описывают окружности, при этом радиус-векторы поворачиваются на угол за время . Для того, чтобы указать, в какую сторону совершается поворот, элементарные повороты изображают в виде вектора . По модулю равен величине угла поворота, а направление подчиняется правилу правого винта (рис. 1.6). Быстроту вращения характеризует угловая скорость .

Р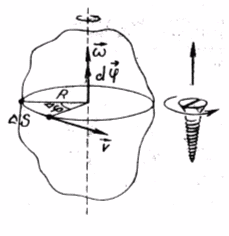ис.1.6Угловой скоростью называется производная от угла поворота по времени. Модуль угловой скорости равен

Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта (рис. 1.6). При равномерном вращении угловая скорость связана с периодом обращения Т  и частотой вращения следующим образом

Модуль угловой скорости выражается в радианах в секунду (рад/с). Быстрота изменения угловой скорости характеризуется угловым ускорением .

Угловым ускорением называется производная от угловой скорости по времени. Модуль углового ускорения равен

При вращении тела вокруг неподвижной оси угловое ускорение также как и угловая скорость направлено вдоль оси вращения. При ускоренном движении эти вектора сонаправлены , при замедленном - противоположны Угловое ускорение измеряется в рад/с². При равномерном вращении

.

При равнопеременном вращении

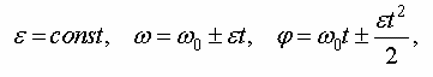где    - начальная угловая скорость.        Знак "+" - при равноускоренном движении.        Знак "-" - при равнозамедленном движении.

28-Рассмотрим тело произвольной формы в “спокойном”, ненагруженном

состоянии. Между его частицами всегда существуют силы взаимодействия,

которые стремятся сохранить его как единое целое, то есть препятствуют

изменению взаимного расположения частиц. При нагружении тела

произвольной внешней нагрузкой силы взаимодействия между частицами

изменяются, появляются дополнительные силы взаимодействия, которые

приводят к изменению взаимного расположения частиц тела, то есть к его

деформации.

Эти дополнительные силы взаимодействия называются внутренними

силами упругости (ВСУ) и являются предметом изучения сопротивления

материалов.

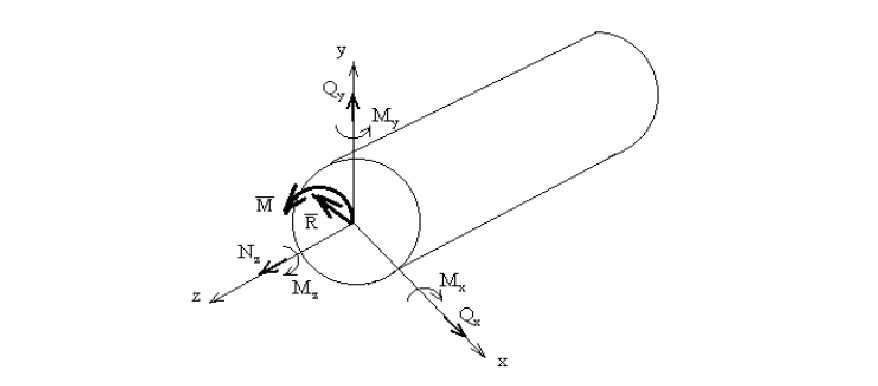
Анализ характера распределения внутренних сил упругости

осуществляется при помощи метода сечений Рассмотрим тело произвольной

формы, нагруженное самоуравновешенной системой сил (рис.1,а). В

интересующем нас сечении мысленно рассечем его плоскостью на две части

4

24-ДИНАМИКА-Динамика изучает виды движения тела в зависимости от приложенных сил.

Аксиомы динамики:

1. всякая изолированная точка находится в состоянии относительного покоя, или равномерного прямолинейного движения до тех пор, пока приложенные силы не выведут её из этого состояния.

2. Ускорение тела прямопропорциональных действующей на тело силе.

3. Если на тело действует система сил, то его ускорение будет складываться из тех ускорений, которые бы тело получало от каждой силы в отдельности.

4. Всякому действию есть есть равное по величине и противоположно направлению противодействие.

Центр тяжести - это точка приложения силы тяжести, при повороте тела центр тяжести не меняет своего положения. Сила инерции - всегда направлена в противоположную сторону ускорению и приложена к связи.

Pu = -ma

При равномерном движении, т.е. когда а=0 сила инерции равна нулю.

При криволинейном движении раскладывается на две составляющие: на нормальную силу и на касательную.

Put=mat=mЕr

Pun=man=mw2r

Метод кинематики: условно прикладывают к телу силу инерции можно считать, что внешние силы реакции связей и сила инерции образуют уравновешенную систему сил.

F+R+Pu=0

25-РАБОТА-Пусть под действием постоянной силы тело прошло прямолинейный путь S. Перемещение тела обусловлено только касательной к траектории составляющей силы F.cos α Н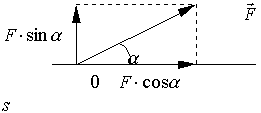ормальная составляющая не вызывает перемещения тела.Механической работой силы называется величина, равная произведению проекции силы на модуль перемещения

При α < 90⁰ работа положительная, при α = 90⁰ A = 0, при α > 90⁰ работа отрицательная - сила тормозит тело. Работа нескольких сил равна сумме работ этих сил по перемещению тела. Если сила переменная, то перемещение разбивают на бесконечно малые отрезки , на которых сила постоянна, затем суммируют

Эффективность совершения работы характеризуется мощностью.

26-МОЩНОСТЬМощность - величина, равная отношению работы к промежутку времени, в течении которого она совершается

Мгновенная мощность равна . При движении тела с постоянной скоростью либо под действием постоянной силы его мощность равна : .

• Коэффициент полезного действия (КПД) равен отношению полезной работы, соверш.нной машиной, к полной работе

• 1 л. с. ≈ 735 Вт . Средняя мощность лошади ≈ 400 Вт , а человека ≈ 100 Вт.

• Энергия - способность системы совершить работу. Виды энергии : механическая, тепловая, электрическая, электромагнитная, химическая, внутренняя (связи) и т.п.

• Механическая энергия: величина, равная максимальной механической работе, которую система может совершить при данных условиях.

• Механическая энергия связанная либо с движением системы, либо с движением е. частей называется кинетической, а энергия, связанная с взаимным расположением частей системы называется потенциальной.

40-ИЗГИБ ВИДЫ ИЗГИБА

-

-

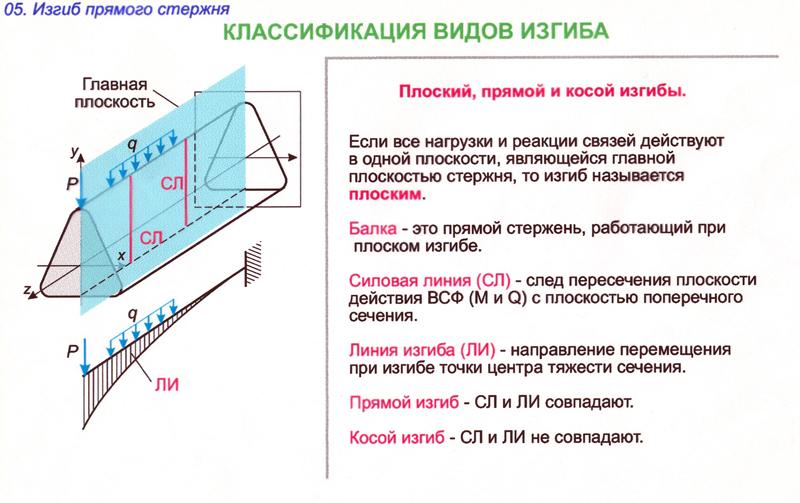
41-ДОПУЩЕНИЯ ПРИ ИЗГИБЕПри плоском поперечном изгибе возникают два вида внутренних силовых факторов (рис. 1):

- изгибающий момент,

- поперечная сила,

которые соответственно определяют нормальные и касательные напряжения (рис 1).

Нормальные напряжения при плоском поперечном изгибе балки (рис. 1) вычисляются ню формуле

, (1)

где  - изгибающий момент в поперечном сечении балки;

- момент инерции сечения относительно нейтральной линии (главной центральной оси ),

- р асстояние от нейтральной линии до точки, в которой определяется напряжение.

Из формулы (1) следует, что нормальные напряжения линейно изменяются по высоте сечения. Они равны нулю на нейтральной линии и достигают максимальной величины в волокнах, наиболее удаленных от нейтральной линии.

При выводе расчетной формулы (1) предполагалось, что волокна материала при поперечном изгибе испытывают только продольное растяжение или сжатие (рис. 2). Это допущение позволяет выразить зависимость между нормальным напряжением и деформацией законом Гука для одноосного растяжения

. (2)

Таким образом, для экспериментального определения нормального напряжения при изгибе достаточно измерить относительное удлинение волокна и произвести расчет напряжений по формуле (2).

Р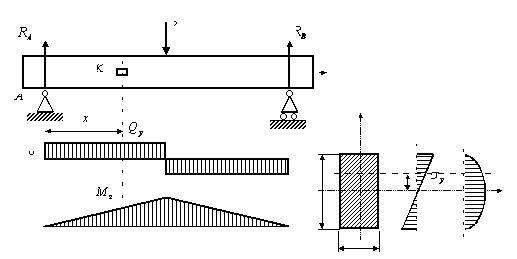ис. 1

Касательные напряжения при поперечном изгибе определяются по формуле

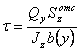, (3)

где - поперечная сила в данном сечении балки (рис. 1);

- статический момент отрезанной части сечения;

- момент инерции всего сечения;

- ширина сечения на уровне точки, в которой определяется напряжение.

В работе экспериментально определяется максимальное касательное напряжение в нейтральном слое сечения (элемент " "). Напряженное состояние в точке нейтрального слоя - чистый сдвиг (рис. 2). При этом по площадкам, на­клоненным к поперечному сечению под углом 45°, действуют главные нормальные напряжения и , по величине равные касательным напряжениям .

Для плоского напряженного состояния относительная деформация в направлении главного напряжения вычисляется по закону Гука

, (4)

где - модуль упругости; - коэффициент Пуассона.

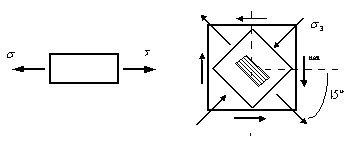
Рис. 2

Так как при чистом сдвиге , то . Таким образом, по измеренной деформации  в направлении действия  представляется возможным рассчитать величину касательного напряжения в точке на нейтральном слое поперечного сечения балки по формуле

. (5)

43-КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ

При плоском поперечном изгибе возникают два вида внутренних силовых факторов (рис. 1):

- изгибающий момент,

- поперечная сила,

которые соответственно определяют нормальные и касательные напряжения (рис 1).