
Шпора по термеху5
.docНормальные напряжения при плоском поперечном изгибе балки (рис. 1) вычисляются ню формуле
![]() , (1)
, (1)
где
![]() -
изгибающий момент в поперечном сечении
балки;
-
изгибающий момент в поперечном сечении
балки;
![]() -
момент инерции сечения относительно
нейтральной линии (главной центральной
оси
-
момент инерции сечения относительно
нейтральной линии (главной центральной
оси
![]() ),
),
![]() -
р асстояние от нейтральной линии до
точки, в которой определяется напряжение.
-
р асстояние от нейтральной линии до
точки, в которой определяется напряжение.
Из формулы (1) следует, что нормальные напряжения линейно изменяются по высоте сечения. Они равны нулю на нейтральной линии и достигают максимальной величины в волокнах, наиболее удаленных от нейтральной линии.
При выводе расчетной формулы (1) предполагалось, что волокна материала при поперечном изгибе испытывают только продольное растяжение или сжатие (рис. 2). Это допущение позволяет выразить зависимость между нормальным напряжением и деформацией законом Гука для одноосного растяжения
![]() . (2)
. (2)
Таким образом, для экспериментального определения нормального напряжения при изгибе достаточно измерить относительное удлинение волокна и произвести расчет напряжений по формуле (2).
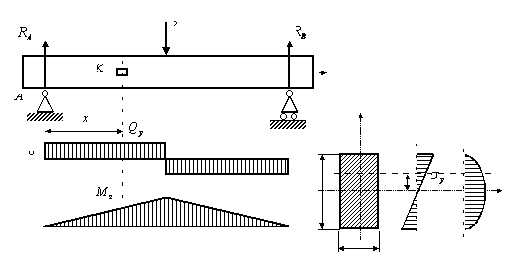
Рис. 1
Касательные напряжения при поперечном изгибе определяются по формуле
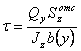 , (3)
, (3)
где
![]() -
поперечная сила в данном сечении балки
(рис. 1);
-
поперечная сила в данном сечении балки
(рис. 1);
![]() -
статический момент отрезанной части
сечения;
-
статический момент отрезанной части
сечения;
![]() -
момент инерции всего сечения;
-
момент инерции всего сечения;
![]() - ширина
сечения на уровне точки, в которой
определяется напряжение.
- ширина
сечения на уровне точки, в которой
определяется напряжение.
В
работе экспериментально определяется
максимальное касательное напряжение
в нейтральном слое сечения (элемент "
![]() ").
Напряженное состояние в точке нейтрального
слоя - чистый сдвиг (рис. 2). При этом по
площадкам, наклоненным к поперечному
сечению под углом 45°, действуют главные
нормальные напряжения
").
Напряженное состояние в точке нейтрального
слоя - чистый сдвиг (рис. 2). При этом по
площадкам, наклоненным к поперечному
сечению под углом 45°, действуют главные
нормальные напряжения
![]() и
и
![]() ,
по величине равные касательным напряжениям
,
по величине равные касательным напряжениям
![]() .
.
Для
плоского напряженного состояния
относительная деформация в направлении
главного напряжения
![]() вычисляется
по закону Гука
вычисляется
по закону Гука
![]() , (4)
, (4)
где
![]() -
модуль упругости;
-
модуль упругости;
![]() -
коэффициент Пуассона.
-
коэффициент Пуассона.
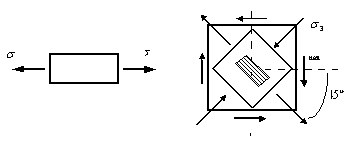
Рис. 2
Так
как при чистом сдвиге
![]() ,
то
,
то
![]() .
Таким образом, по измеренной деформации
.
Таким образом, по измеренной деформации
![]() в
направлении действия
в
направлении действия
![]() представляется
возможным рассчитать величину касательного
напряжения в точке на нейтральном слое
поперечного сечения балки по формуле
представляется
возможным рассчитать величину касательного
напряжения в точке на нейтральном слое
поперечного сечения балки по формуле
![]() . (5)
. (5)
44-ГИПОТЕЗЫ ПРОЧНОСТИ-
Гипотеза наибольших линейных деформаций (II теория прочности)
В основу теории наибольших линейных деформаций (Мариотт, 1682 г.) положена гипотеза о преимущественном влиянии наибольших по абсолютной величине линейных деформаций.
Согласно данной теории прочности опасное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее из относительных удлинений достигает опасной величины, соответствующей пределу прочности при простом растяжении.
Максимальные относительные деформации в соответствии с обобщенным законом Гука (3.36)
|
|
(9.20) |
|
|
(9.21) |
При простом растяжении
|
|
(9.22) |
Предельное значение относительной деформации при растяжении
|
|
(9.23) |
На основании сформулированной гипотезы, имеем
![]()
или с учетом (9.20), (9.23)
|
|
(9.24) |
Сравнивая с условием наступления предельного состояния (9.2), получим эквивалентное напряжение по II теории прочности:
|
|
(9.25) |
Условие прочности в соответствии с (9.1) имеет следующий вид:
|
|
(9.26) |
|
|
(9.27) |
Из (9.26), (9.27) вытекает, что простое растяжение более опасно нежели сложное. Опыты этого не подтверждают. В связи с этим данная теория для расчета деталей не используется.
42-РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ

46-РАСЧЕТ НА УСТОЙЧИВОСТЬ ФОРМУЛА ЭЙЛЕРА-
|
Для шарнирно
закрепленного, центрально-сжатого
стержня постоянного сечения (рис.8.2).
I Формула Эйлера имеет вид:
Выражение
"приведенная длина" означает,
что в формуле Эйлера с помощью
коэффициента
Коэффициент
приведения длины
Формула Эйлера
применима только о пределах выполнения
закона Гука, когда критическое
напряжение
где
Значение предельной
гибкости
|
39-КРУЧЕНИЕ УСЛОВИЕ ПРОЧНОСТИ И ЖЕСТКОСТИ
Расчеты на прочность и жесткость при кручении
Принципы расчетов на прочность, изложенные в главе 4 применительно к одноосному растяжению и сжатию, полностью справедливы и для случая кручения бруса. При кручении расчеты на прочность также делятся на проектировочные и поверочные. В основе расчетов лежит условие прочности
|
|
(7.34) |
где τmax - максимальное касательное напряжение в брусе, определяемое по вышеприведенным уравнениям в зависимости от формы сечения; [τ] - допускаемое касательное напряжение, равное части предельного напряжения для материала детали - предела прочности τв или предела текучести τт. Коэффициент запаса прочности устанавливается из тех же соображений, что и при растяжении. Например, для вала полого круглого поперечного сечения, с внешним диаметром D и внутренним диаметром d, имеем
|
|
(7.35) |
где α=d/D - коэффициент полости сечения.
Условие жесткости такого вала при кручении имеет следующий вид:
|
|
(7.36) |
где [φo] - допускаемый относительный угол закручивания.
27- СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ, раздел механики твердого тела, изучающий напряжения и деформации, которые обусловлены силами, действующими на твердые тела – элементы конструкции. Эту дисциплину можно характеризовать и как науку о методах расчета элементов конструкции на прочность, жесткость и устойчивость.
Напряжение, создаваемое в твердом теле внешними нагрузками, есть мера (с размерностью силы на единицу площади) интенсивности внутренних сил, действующих со стороны одной, мысленно отсекаемой, части тела на другую, оставшуюся (метод сечений). Внешние нагрузки вызывают деформацию тела, т.е. изменение его размеров и формы. В сопротивлении материалов исследуются соотношения между нагрузками, напряжениями и деформациями, причем исследования ведутся, с одной стороны, путем математического вывода формул, связывающих нагрузки с вызываемыми ими напряжениями и деформациями, а с другой – путем экспериментального определения характеристик материалов, применяемых в строениях и машинах.
29-
НапряженияМ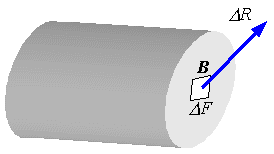 ерой
интенсивности внутренних сил,
распределенных по сечениям, служат
напряжения – усилия, приходящиеся на
единицу площади сечения. Выделим в
окрестности точки B
малую площадку ΔF
(рис. 3.1). Пусть ΔR
- равнодействующая внутренних сил,
действующих на эту площадку. Тогда
среднее значение внутренних сил,
приходящихся на единицу площади ΔF
рассматриваемой площадки, будет равно:
ерой
интенсивности внутренних сил,
распределенных по сечениям, служат
напряжения – усилия, приходящиеся на
единицу площади сечения. Выделим в
окрестности точки B
малую площадку ΔF
(рис. 3.1). Пусть ΔR
- равнодействующая внутренних сил,
действующих на эту площадку. Тогда
среднее значение внутренних сил,
приходящихся на единицу площади ΔF
рассматриваемой площадки, будет равно:
![]()
Рис. 3.1. Среднее напряжение на площадке
Величина pm
называется средним
напряжением. Она
характеризует среднюю интенсивность
внутренних сил. Уменьшая размеры площади,
в пределе получим![]()
Величина p называется истинным напряжением или просто напряжением в данной точке данного сечения.
Единица напряжения – паскаль, 1 Па = 1 Н/м2. Так как реальные значения напряжений будут выражаться очень большими числами, то следует применять кратные значения единиц, например МПа (мегапаскаль) 1 МПа= 106 Н/м2.
Напряжения, как и силы, являются векторными величинами. В каждой точке сечения тела полное напряжение p можно разложить на две составляющие (рис. 3.2):
1) составляющую, нормальную к плоскости сечения. Эта составляющая называется нормальным напряжением и обозначается σ;
2) составляющую, лежащую(в плоскости сечения. Эта составляющая обозначается τ и называется касательным напряжением. Касательное напряжение в зависимости от действующих сил может иметь любое направление в плоскости сечения. Для удобства τ представляют в виде двух составляющих по направлению координатных осей. Принятые обозначения напряжений показаны ни рис. 3.2
У нормального напряжения ставится индекс, указывающий какой координатной оси параллельно данное напряжение. Растягивающее нормальное напряжение считается положительным, сжимающее – отрицательным. Обозначения касательных напряжений имеют два индекса: первый из них указывает, какой оси параллельна нормаль к площадке действия данного напряжения, а второй – какой оси параллельно само напряжение. Разложение полного напряжения на нормальное и касательное имеет определенный физический смысл. Нормальное напряжение возникает, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц материала по плоскости сечения.
Р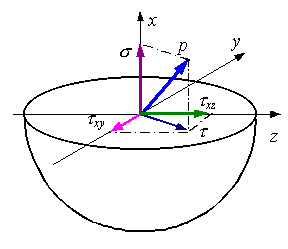 ис.
3.2. Разложение вектора полного напряжения
ис.
3.2. Разложение вектора полного напряжения
Если мысленно вырезать вокруг какой-нибудь точки тела элемент в виде бесконечно малого кубика, то по его граням в общем случае будут действовать напряжения, представленные на рис. 3.3. Совокупность напряжений на всех элементарных площадках, которые можно провести через какую-либо точку тела называется напряженным состоянием в данной точке.
Вычислим сумму моментов всех элементарных сил, действующих на элемент (рис.3.3), относительно координатных осей, так, например, для оси x с учетом равновесия элемента, имеем:
![]()
Повторяя указанные
действия для других осей, получим закон
парности касательных напряжений:
![]()
который формулируется следующим образом: составляющие касательных напряжений на двух взаимно перпендикулярных площадках, перпендикулярные общему ребру, равны по величине и противоположны по знаку, то есть либо обе направлены к ребру либо обе направлены от ребра.
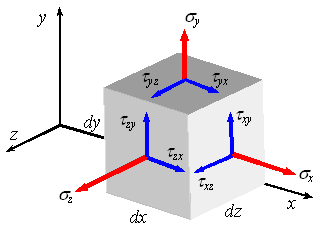
Рис. 3.3. Система напряжений в точке
3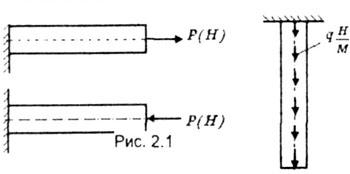 0-
РАСТЯЖЕНИЕ И СЖАТИЕ
Центральным растяжением (сжатием)
называется такой вид деформации, при
котором в поперечном сечении бруса
возникает только продопьная сила
(растягивающая или сжимающая), а все
остальные внутренние усилия равны
нулю.(рис.2.1) ПОСТРОЕНИЕ ЭПЮР ПРОДОЛЬНЫХ
СИЛ N Рис. 2.1
Продольная сила
- это внутреннее усилие, которое возникает
между отдельными частями элемента под
действием внешних сип (центрально-сжимающих
или центрально-растягивающих). Для
определения продольной силы используется
метод
сечений.
Растяжение обозначается плюсом (+),
сжатие минусом (-). (рис.2.2). В соответствии
с методом сечений; разрезаем, отбрасываем,
заменяем, уравновешиваем
0-
РАСТЯЖЕНИЕ И СЖАТИЕ
Центральным растяжением (сжатием)
называется такой вид деформации, при
котором в поперечном сечении бруса
возникает только продопьная сила
(растягивающая или сжимающая), а все
остальные внутренние усилия равны
нулю.(рис.2.1) ПОСТРОЕНИЕ ЭПЮР ПРОДОЛЬНЫХ
СИЛ N Рис. 2.1
Продольная сила
- это внутреннее усилие, которое возникает
между отдельными частями элемента под
действием внешних сип (центрально-сжимающих
или центрально-растягивающих). Для
определения продольной силы используется
метод
сечений.
Растяжение обозначается плюсом (+),
сжатие минусом (-). (рис.2.2). В соответствии
с методом сечений; разрезаем, отбрасываем,
заменяем, уравновешиваем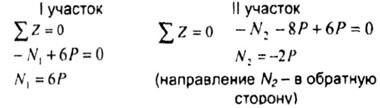
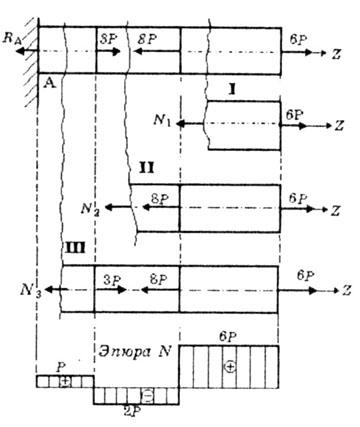
![]()
-
Скачок в эпюре N равен приложенной в этом сечении сосредоточенной силе.
В сечении "А" (заделка) есть реакция RA, которую можно найти из формулы:
![]() Но
проще идти со свободного конца, и затем
найти реакцию RA
по эпюре в точке А: RA
= P
Но
проще идти со свободного конца, и затем
найти реакцию RA
по эпюре в точке А: RA
= P
31-если совокупность некоторых сил, приложенных к небольшой части поверхности тела, заменить статически эквивалентной системой других сил, то такая замена не вызовет существенных изменений в условиях нагружения частей тела, достаточно удаленных от мест приложения исходной системы сил.
Принятие этого принципа означает условие рассматривать только те части тела, которые достаточно удалены от места приложения нагрузки. Расчетом деталей в местах их контакта занимается самостоятельная научная дисциплина – математическая теория упругости. На рис. 1.7 представлена иллюстрация принципа Сен-Венана на простейшем примере. Из рисунка видно, что замена распределенной нагрузки статически эквивалентной сосредоточенной силой не окажет существенного влияния на условия нагружения части бруса, удаленной на расстояние не менее 3...5·t от правой границы действия распределенной нагрузки, где t - наибольший размер поперечного сечения бруса.
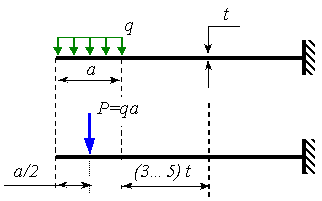
Рис. 1.7. Иллюстрация принципа Сен-Венана
32-ПРОДОЛЬНАЯ И ПОПЕРЕЧНАЯ ДЕФОРМАЦИЯПод действием внешних сил тела меняют свою форму и размеры. Такие изменения называются деформациями. Различаются упругие и пластические деформации. Если после прекращения приложенных сил деформация исчезает, то деформация является упругой, а если не исчезает - пластической. Вообще-то упругость или пластичность деформации зависит не только от материала тела, но и от величины приложенных сил. Если сила, отнесенная к единице площади, не превосходит так называемого предела упругости, то деформация будет упругой, в противном случае – пластической.
Будем считать тела идеально упругими,
которые могут претерпевать только
упругие деформации. Для этого будем
считать, что приложенные нами силы не
превосходят предела упругости. Причем
ограничимся изучением только малых
деформаций, т.е. таких, которые подчиняются
закону Гука - деформации пропорциональны
вызывающим их силам.ЗАКОН
ГУКА-, устанавливает
линейную зависимость между упругой
деформацией
твердого
тела
и приложенным мех. напряжением. Напр.,
если стержень длиной l и поперечным
сечением 5 растянуть продольной силой
F, то удлинение стержня![]() , где Е- модуль упругости (модуль Юнга),
зависящий от материала стержня. Для
деформации
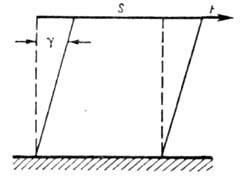
сдвига (см. рис.) Г. з. имеет вид:
, где Е- модуль упругости (модуль Юнга),
зависящий от материала стержня. Для
деформации
сдвига (см. рис.) Г. з. имеет вид:![]() где
где![]() = F/S-касат. напряжение (F-касат. сила,
S-площадь сдвигающихся слоев),
= F/S-касат. напряжение (F-касат. сила,
S-площадь сдвигающихся слоев),![]() -угол
сдвига (относит. сдвиг), G-модуль сдвига,
зависящий от материала тела. Г. з.
справедлив лишь при напряжениях и
деформациях,
не превосходящих нек-рых предельных
для данного материала значений. Установлен
Р. Гуком в 1650.
-угол
сдвига (относит. сдвиг), G-модуль сдвига,
зависящий от материала тела. Г. з.
справедлив лишь при напряжениях и
деформациях,
не превосходящих нек-рых предельных
для данного материала значений. Установлен
Р. Гуком в 1650.
33-Коэффициент запасаПРОЧНОСТИ. Условие прочности
Отношение предельного напряжения к наибольшему расчетно- му называют коэффициентом запаса прочности
n= σпред/σmax(n=tпред/tmax).
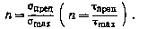
Коэффициент запаса прочности (фактический) должен быть не меньше требуемого (заданного, допускаемого, нормативного) для данного элемента конструкции n>>[n] Приведенное неравенство является условием прочности. Во многих случаях удобнее вести расчет на прочность, пользуясь понятием о допускаемом напряжении, которое равно отношению предельного напряжения к требуемому коэффициенту запаса прочности

При использовании понятия о допускаемом напряжении условие прочности представляют в виде:
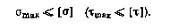
* Предел прочности иногда называют временным сопротивлением и обозначают σв или σв. ** В специальной, в частности, справочной литературе зачастую не разграничивают обозначений физических и условных пределов текучести, применяя для тех и других единое обозначение σт (соответственно σтр и σатс).
Если максимальное рабочее напряжение значительно меньше до- пускаемого, конструкция является излишне тяжелой, неэкономич- ной. Незначительное превышение рабочего напряжения над допускае- мым неопасно для прочности конструкции, так как требуемый (нор- мативный) коэффициент запаса имеет для пластичного материала даже при наиболее благоприятных условиях работы и высокой точности расчета значение порядка 1,3-1,5, а для хрупкого мате- риала не ниже 3-4. Для пластичного материала значение коэффи- циента запаса указано по отношению к пределу текучести, а для хрупкого - к пределу прочности.
Все сказанное о коэффициентах запаса и условиях прочности относится в основном к расчету по опасной точке (см. стр. 5). При расчете по предельным нагрузкам под коэффициентом запаса сле- дует понимать отношение нагрузки (силы, момента пары сил и т. п.), при которой наступает переход в предельное состояние (РПред, M пред и т. п.), к фактически действующей нагрузке n=Pпред/P (n = M пред /M). Условие прочности удобнее всего представлять в виде: п > [п], где [п]-требуемый (нормативный) коэффициент запаса прочности. Несмотря на тождественность формы записи условий прочности при расчетах по опасной точке и по предельной нагрузке, эти расчеты принципиально различны.
34-УСЛОВИЯ ПРОЧНОСТИ ПРИ РАСТЯЖЕНИИ СЖАТИИ Определив напряжение в опасном сечении растянутого (сжатого) стержня по формуле 4.3 и установив допускаемое напряжение в соответствии с соображениями, изложенными выше, можно произвести оценку прочности стержня.
Для этого необходимо
фактические напряжения в опасном сечении
стержня сопоставить с допускаемыми:
![]()
Здесь имеется в виду допускаемое напряжение или на растяжение, или на сжатие в зависимости от того, с каким случаем мы имеем дело - с растяжением или сжатием.
Неравенство (4.11) называется условием прочности при растяжении (сжатии). Пользуясь этим условием, можно решать следующие задачи:
1. Проверять прочность стержня, т. е. определять по заданным нагрузке и размерам поперечного сечения стержня фактические напряжения и сравнивать их с допускаемыми. Фактические напряжения не должны отклоняться от допускаемых более чем на ±5%. Перенапряжение больше этого значения недопустимо с точки зрения прочности, а недонапряжение свидетельствует о перерасходе материала.
2.
Определять размеры поперечного сечения
стержня (по
известным нагрузке и допускаемому
напряжению), требуемые по условию его
прочности:
![]()
3.
Определять допускаемую продольную силу
по заданным размерам поперечного сечения
стержня и известному допускаемому
напряжению:
![]()
Определив допускаемую продольную силу и установив связь между продольной силой и нагрузкой (методом сечений), можно определить и допускаемую нагрузку.
Следует иметь в виду, что сжатые стержни кроме расчета на прочность в наиболее ослабленном сечении должны также рассчитываться на устойчивость, так как при определенном значении сжимающей силы может произойти выпучивание (продольный изгиб) сжатого стержня.

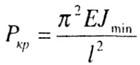 где Е - модуль продольной упругости
материала стержня; Jmin
- минимальный момент инерции поперечного
сечения стержня. Для стержней с другими
видами закрепления формулу Эйлера
записывают в виде:
где Е - модуль продольной упругости
материала стержня; Jmin
- минимальный момент инерции поперечного
сечения стержня. Для стержней с другими
видами закрепления формулу Эйлера
записывают в виде:
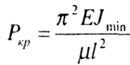 где
где
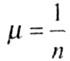 На рис. 8.2 показаны наиболее часто
встречающиеся на практике случаи
закрепления концов стержня и
соответствующие им значения коэффициента
На рис. 8.2 показаны наиболее часто
встречающиеся на практике случаи
закрепления концов стержня и
соответствующие им значения коэффициента
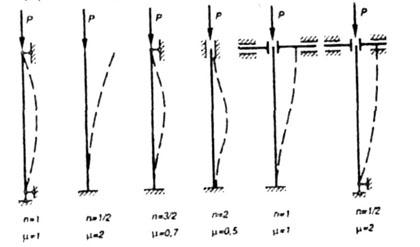 Рис. 8.2
Рис. 8.2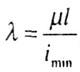
 -
минимальный радиус инерции (геометрическая
характеристика сечения
-
минимальный радиус инерции (геометрическая
характеристика сечения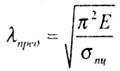 Так, для малоуглеродистой
стали, если принять Е = 2x105
МПа,
Так, для малоуглеродистой
стали, если принять Е = 2x105
МПа,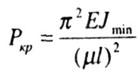 применима в случае, если гибкость
стержня находится в пределах
применима в случае, если гибкость
стержня находится в пределах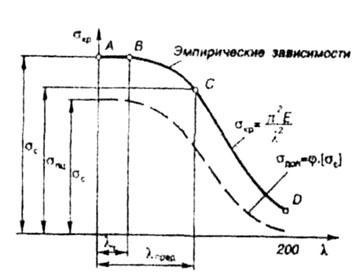 Рис. 8.3 Для
малоуглеродистой стали этот диапазон
равен
Рис. 8.3 Для
малоуглеродистой стали этот диапазон
равен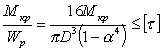 ,
,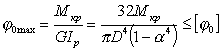 ,
,