
Рабочие тетради №2-9 / Рабочая тетрадь_7
.doc|
Д
101
где
Сумма
частных коэффициентов эластичности
Пример 7.6. Имеются некоторые данные о среднегодовой стоимости ОПФ (СОПФ), уровне затрат на реализацию продукции (ЗРП) и стоимости реализованной продукции (РП) (табл. 7.6). Считая зависимость между этими показателями линейной, определить уравнение связи; вычислить множественный и частные коэффициенты корреляции, оценить значимость модели. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
102 Таблица 7.6
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
С
103
Выразим из 1-го уравнения системы a0 = 29,4 – 6,6·a1 – 9·a2. Подставив во 2-е уравнение это выражение, получим:
Далее подставляем в 3-е уравнение вместо a0 и a1 полученные выражения и решаем его относительно a2 с точностью не менее 3-х знаков после запятой. Итак: a0 = 12,508; a1 = 2,672; a2 = – 0,082; уравнение множественной регрессии имеет вид
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
О
104
Множественный коэффициент корреляции
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П
105
Вычислим стандартизованные коэффициенты уравнения множественной регрессии:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О
106
т.е. вариация результативного признака объясняется главным образом вариацией фактора x1. Вычислим частные коэффициенты эластичности:
Проверим адекватность модели на основе критерия Фишера:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
106 106 107 Универсальным показателем тесноты связи является теоретическое корреляционное отношение:
где
|
|
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
Т
108 Оценка связи на основе теоретического корреляционного отношения (шкала Чеддока)
Для парной линейной зависимости теоретическое корреляционное отношение равно линейному коэффициенту корреляции (η = |r|). Аналогично для множественной линейной зависимости – η = R.
|
|
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|

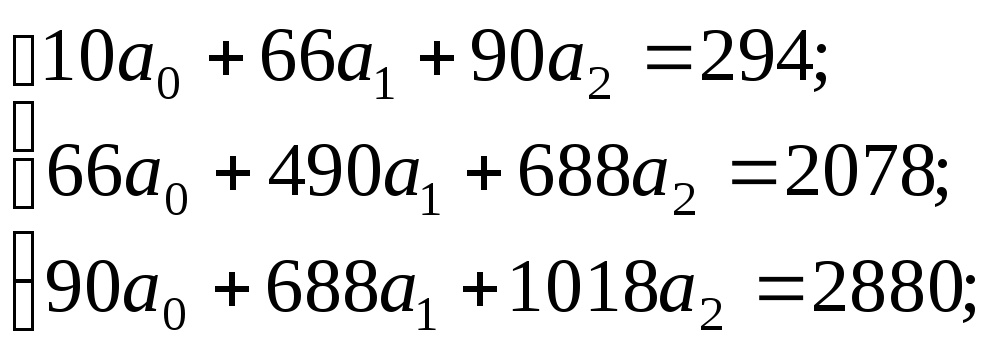

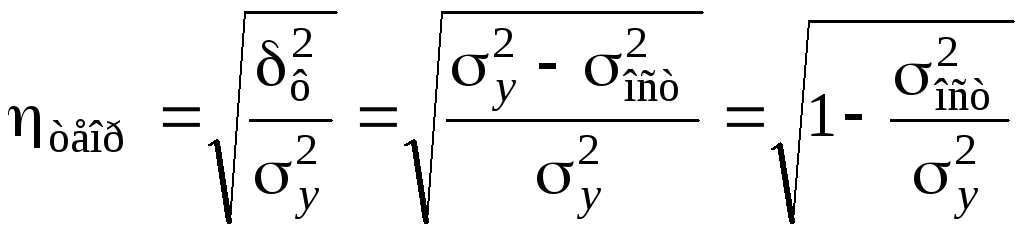 , (7.41)
, (7.41)