2.9. Корреляционно-регрессионный анализ как способ изучения стохастических взаимосвязей

В современных условиях, характеризующихся применением в производстве сложной техники и технологии, усилением влияния рыночных факторов, нестабильности некоторых процессов в народном хозяйстве разработка научно обоснованных решений должна проводиться на основе системного и комплексного изучения финансово-хозяйственной деятельности предприятия. При этом нужно учитывать воздействие множества субъективных и объективных, постоянно действующих и случайных факторов, связь которых с результирующим показателем зачастую является неопределенной, вероятностной. Причем в зависимости от сочетания разных факторов степень их воздействия на величину результирующего показателя будет неодинаковой.

Достаточно широкое применение в экономических исследованиях получил корреляционно-регрессионный анализ, который позволяет углубить знания об изучаемых явлениях, расширить факторный анализ, определить степень воздействия каждого фактора на изучаемый объект, что дает возможность комплексно и объективно оценить итоги деятельности предприятия, наиболее полно выявить резервы, точнее обосновать планы и управленческие решения.

Основным условием применения корреляционно-регрессионного анализа является наличие достаточно большого массива значений изучаемых показателей, имеющих количественное измерение. Корреляционно-регрессионный анализ в комплексе использует регрессионный анализ, предназначенный для выбора формы связи, типа модели и определения расчетных значений результирующего показателя, и корреляционный анализ, который позволяет измерить тесноту связи между варьирующими переменными и оценить факторы, оказывающие наибольшее влияние на результирующий показатель.

Корреляция может быть парной и множественной.

Парная корреляция – это связь между двумя показателями, один из которых является фактором, а другой – результирующим показателем.

Множественная корреляция – связь между несколькими факторами и одним результирующим показателем.

Основные этапы корреляционного анализа:

1. Выделяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются факторы, наиболее существенные для корреляционного анализа.

2. Собирается исходная информация по каждому факторному и результирующему показателям. Информация должна быть достоверной, однородной и соответствующей закону нормального распределения. Одно из условий корреляционного анализа – однородность исследуемой информации относительно распределения ее около среднего уровня.

3. Изучается характер взаимосвязей и моделируется связь между факторами и результирующим показателем, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно отражает сущность исследуемой зависимости.

Зависимость результирующего показателя от определяющих его факторов можно выразить уравнением парной регрессии: . Если связь между результативным и факторными показателями носит криволинейный характер, то могут быть использованы степенная, логарифмическая, параболическая, гиперболическая и другие функции.

4. Проводится расчет основных показателей связи корреляционного анализа: уравнение связи, коэффициенты корреляции, детерминации, эластичности и др.

Для измерения тесноты связи между факторными и результирующим показателями исчисляется коэффициент корреляции (r). При прямолинейной форме связи он рассчитывается по формуле:

, (2.41)

где y – индивидуальные значения результирующего показателя;

x – индивидуальные значения факторного показателя;

n – количество значений.

Величина коэффициента корреляции находится в пределах от -1 до +1. Наличие определенной зависимости между двумя переменными характеризуется значениями, близкими к +1 или -1.

Если η (r) = 0, то связь между показателями отсутствует;

если 0,7 - 0,9, то связь высокая;

если η (r) = 1, то связь функциональная (детерминированная);

если η (r) – отрицательная величина, то связь между показателями обратная.

Альтернативным показателем степени зависимости между двумя переменными является коэффициент детерминации, представляющий собой возведенный в квадрат коэффициент корреляции (r²). Коэффициент детерминации выражается в процентах и отражает величину изменения результирующего показателя (у) за счет изменения другой переменной – факторного показателя (х).

При измерении тесноты связи при криволинейной форме зависимости используется корреляционное отношение, формула которого имеет следующий вид:

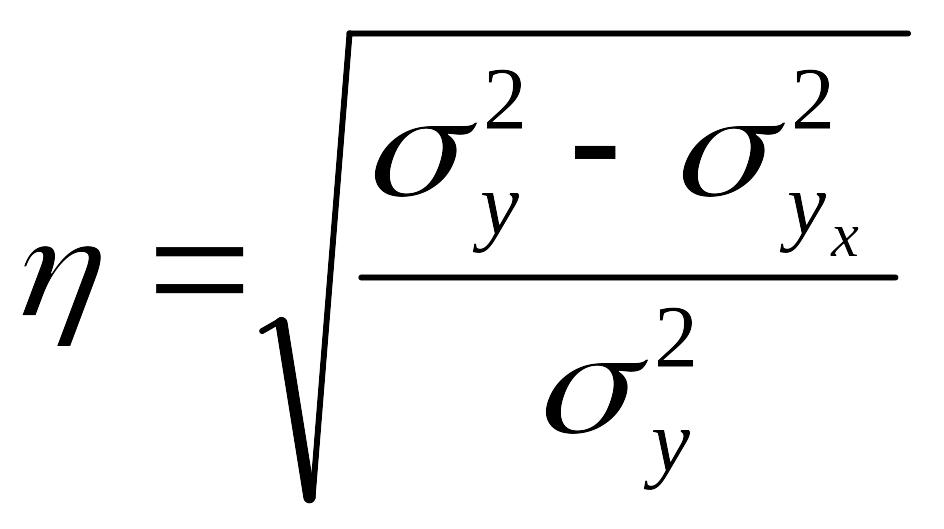, (2.42)

где ; (2.43)

. (2.44)

Данная формула является универсальной. Ее можно применять для исчисления коэффициента корреляции при любой форме зависимости.

Для характеристики относительного изменения показателей эффективности производства рассчитываются коэффициенты эластичности (эi), которые позволяют измерить в процентах изменение функции при изменении каждого фактора-аргумента на 1%.

Эi=аi*(Хi/Yi), (2.45)

где аi – коэффициент регрессии i-го фактора в модели;

Хi, Yi – среднеарифметические значения i-го фактора-аргумента и функции Yi.

Выделение факторов, в которых заложены наибольшие резервы, проводится с помощью β-коэффициентов, которые учитывают степень вариации показателей и показывают, на сколько среднеквадратических отклонений изменилась бы величина результирующего показателя при увеличении на среднеквадратическое отклонение каждого из аргументов:

Βi=аi(σ xi/ σ yi), (2.46)

где σ xi, σ yi – среднеквадратические отклонения i-го фактора-аргумента и функции Yi.

Многофакторный корреляционно-регрессионный анализ можно проводить на ПЭВМ типа IBM PC/AT в программе Microsoft Office Excel.

Рассмотрим пример корреляционно-регрессионного анализа добычи нефти с помощью программы Microsoft Office Excel, в котором были использованы следующие показатели:

– среднесуточный дебит одной скважины по нефти q, т/сут.;

– удельный расход электроэнергии на добычу 1 т нефти R_Э/Э, кВт/т;

– удельный расход химического реагента УR_ХР, руб./т;

– обводненность нефти Об, %;

– удельный вес материальных затрат в структуре себестоимости УВ_МЗ, %;

– производительность труда ПТ, т/ чел.;

– удельная численность УЧ, чел./ скв.;

– удельный вес заработной платы в структуре себестоимости УВ_ЗП, %

– коэффициент эксплуатации скважин К_Э;

– коэффициент интенсивного использования скважин К_ИИ;

– коэффициент интегрального использования действующего фонда скважин К_iД.

В таблице 2.7 приведены исходные данные для корреляционно-регрессионного анализа себестоимости добычи 1 тонны нефти.

В программе рассчитываются коэффициенты парной и множественной корреляции, проводится дисперсионный анализ моделей. Выводятся на печать средние значения всех переменных, стандартные отклонения, коэффициенты парной и множественной корреляции, коэффициенты регрессии, стандартные ошибки коэффициентов регрессии, значения критериев Фишера и Стьюдента. Эта информация позволяет сделать полный статистический анализ моделей [17].

Значимость регрессионной модели в целом проверяется по критерию Фишера (F-критерию). Расчетные значения F-критерия выводятся на печать, и проводится сравнение расчетного значения с критическим, которое находится по таблицам распределения Фишера. При этом задаются определенным уровнем значимости α. Во всех расчетах принят уровень значимости α = 0,90.

Число степеней свободы числителя и знаменателя дисперсионного отношения выводится на печать. Если расчетное значение критерия Фишера (F_Р) больше критического (F_КР), то регрессионная модель считается значимой.

Как правило, значимой модели соответствует значимый коэффициент множественной корреляции R. Однако в случаях, близких к критическим (F_Р = F_КР), это может не выполняться. Задача определения значимости коэффициента множественной корреляции решается самостоятельно. Для этого используют таблицы критических значений коэффициентов множественной корреляции.

Таблица 2.7 Исходные данные для экономико-математического моделирования себестоимости добычи нефти

Факторы	Себестоимость 1 т нефти, руб./т	Среднесут. дебит по нефти, т/сут.	Уд. расход электроэнергии, кВт-ч./т	Производи-тельность труда, т./чел.	Уд. расход химического реагента, руб/т	Обводненность, %	Уд. численность, чел./скв.	Уд. вес ЗП, %	Уд. вес МЗ, %	Коэф-т эксплуатации скважин	Коэф-т интенсивного использования скважин	Коэфф-т интегрального использования действующего фонда скважин
Обозна- чение Период	CС	qсут	Rэ/э	ПТ	УRХР	Об	УЧ	УВЗП	УВМЗ	КЭ	КИИ	КiД
дек.03	2 124,1	68,67	31,19	64,86	15,67	21,482	23,4	9,52	12,71	0,957	0,988	0,946
ноя.03	1 639,9	69,51	30,81	63,74	14,26	21,96	23,8	13,76	9,41	0,974	1,000	0,974
окт.03	1 629,1	65,98	30,08	65,58	14,03	21,384	22,3	12,18	8,12	0,981	0,949	0,931
сен.03	1 578,8	67,94	25,59	63,68	12,58	21,684	23,4	11,51	6,78	0,966	0,978	0,945
авг.03	1 586,5	68,24	27,65	66,89	12,93	21,27	23,1	12,38	6,85	0,951	0,982	0,934
июл.03	1 566,3	68,82	17,31	66,92	12,41	20,618	23,2	11,80	5,62	0,961	0,990	0,951
июн.03	2 036,4	65,37	23,72	60,34	14,26	21,623	23,4	13,67	6,26	0,961	0,940	0,903
май.03	1 982,0	60,58	26,20	57,09	12,96	21,016	23,9	22,14	8,78	0,978	0,720	0,704
апр.03	2 022,1	62,19	27,97	53,58	13,33	19,627	24,4	17,03	9,21	0,955	0,895	0,855
мар.03	2 195,5	60,11	28,54	54,29	13,66	20,96	24,4	12,41	7,52	0,975	0,865	0,843
фев.03	2 352,3	54,85	31,78	46,42	13,86	21,858	23,1	13,03	6,32	0,933	0,789	0,736
янв.03	2 285,5	55,46	31,61	54,73	13,17	21,09	22,4	11,00	7,63	0,949	0,798	0,757
дек.02	2 123,8	62,42	29,77	56,06	12,83	20,633	20,2	12,33	7,56	0,952	1,000	0,952
ноя.02	2 715,9	63,00	28,52	55,35	15,60	21,52	19,9	9,85	8,23	0,969	0,986	0,955
окт.02	1 850,4	61,83	25,98	56,89	12,56	22,365	19,9	12,85	6,63	0,956	0,978	0,935
сен.02	2 275,0	69,45	24,06	54,81	13,25	22,662	19,9	13,39	5,80	0,963	0,974	0,938
авг.02	2 132,8	56,74	23,27	54,27	12,27	22,136	20,1	27,88	7,57	0,935	0,989	0,925
июл.02	3 066,7	54,25	18,92	52,26	13,33	21,483	20,4	7,53	3,70	0,941	0,874	0,822
июн.02	2 115,4	47,80	28,40	39,19	12,48	25,092	21,9	29,32	8,60	0,942	0,823	0,775
май.02	2 456,1	49,18	31,74	39,92	13,70	28,575	22,3	17,64	11,11	0,982	0,768	0,754
апр.02	2 110,4	47,55	37,63	37,36	12,99	27,518	23,1	34,48	15,55	0,991	0,764	0,757
мар.02	3 129,3	47,41	33,02	38,15	15,32	26,649	22,6	10,83	6,49	0,978	0,768	0,751
фев.02	2 257,9	47,78	36,73	35,64	14,26	26,824	23,2	22,86	17,50	0,972	0,773	0,751
янв.02	2 052,9	49,14	36,27	41,65	13,33	26,294	23,3	27,00	20,65	0,949	0,782	0,742

В зависимости от количества переменных в модели находится критическое значение коэффициента множественной корреляции:

R_кр = R(α, n, k), (4.1)

где α – уровень значимости;

n – объем выборки;

k – количество переменных в модели.

Если расчетное значение коэффициента множественной корреляции (R) больше критического значения (R_кр), то R_p считается статистически значимым коэффициентом.

Если модель в целом значима, то ее можно использовать для дальнейшего экономического анализа. Однако в модели отдельные коэффициенты регрессии могут быть значимы или незначимы. Вывод о значимости коэффициентов регрессии проводится по t-критерию Стьюдента.

В программе на печать выводится расчетное значение t-критерия, которое определяется как отношение данного коэффициента регрессии к стандартной ошибке этого коэффициента. Расчетное значение t-критерия сравнивается с критическим значением t_кр, которое находится по таблицам распределения Стьюдента, t_кр = t(α, n-1), где α – уровень значимости, n – объем выборки. Если t_p > t_кр, то данный коэффициент регрессии считается статистически значимым.

Даже если модель в целом незначима, незначимы и коэффициенты регрессии α_i, все равно из нее можно извлечь полезную информацию.

Проверка значимости коэффициентов парной корреляции Ч_р может быть завершена с помощью таблицы критических значений для коэффициентов парной корреляции, Ч_кр = Ч(α, n-2), где α – уровень значимости, n – объем выборки. Если расчетное значение коэффициента парной корреляции больше критического значения, т.е. Ч_р > Ч_кр, то расчетный коэффициент парной корреляции считается статистически значимым [23].

Расчетные значения коэффициентов парной корреляции приведены в таблице 2.8.

Таблица 2.8 Расчетные значения коэффициентов парной корреляции

№ п/п	Факторы-аргументы	Себестоимость добычи 1 т нефти, Сс
1	qсут	-0,5648
2	Rэ/э	0,1117
3	ПТ	-0,5778
4	Об	0,3268
5	УЧ	-0,3528
6	УВЗП	-0,1269
7	УRХР	0,4482
8	УВМЗ	-0,0808
9	КЭ	-0,0620
10	КИИ	-0,4177
11	КiД	-0,4364

В результате многофакторного корреляционно-регрессионного анализа между себестоимостью добычи 1 т нефти и показателями организационно-технического уровня производства и изменения природно-климатических условий добычи нефти и газа были получены статистически значимые зависимости линейного вида, представленные ниже.

1) С = 1237,645 – 29,714 q_сут + 196,606 УR_ХР

R_Р = 0,723; F_Р = 11,806 при n₁ = 2, n₂ = 21

R_КР = 0,398; F_КР = 2,57

2) С = 3410,947 – 23,895 ПТ

R_Р = 0,578; F_Р = 11,025 при n₁ = 1, n₂ = 22

R_КР = 0,271; F_КР = 2,95

3) С = 847,443 + 8,472 Об – 1567,787 К_ИИ +184,063 УR_ХР

R_Р = 0,604; F_Р = 3,827 при n₁ = 3, n₂ = 20

R_КР = 0,326; F_КР = 2,27

Проверка на значимость уравнений регрессии по критерию Фишера и коэффициентов множественной корреляции показала значимость практически всех характеристик. Результаты регрессионного анализа моделей себестоимости добычи 1 тонны нефти представлены в таблицах 2.9, 2.10 и 2.11.

Таблица 2.9 Результаты регрессионного анализа модели 1 себестоимости добычи