12. Функція розподілу, щільність. Числові характеристики неперервних випадкових величин
Функцією розподілу F(x) (інтегральною) називають ймовірність того, що випадкова величина X прийме значення менше x:
Диференціальною функцією розподілу або щільністю ймовірностей неперервної випадкової величини називають похідну першого порядку від її інтегральної функції розподілу і позначають :
Теорема 1. Ймовірність того, що неперервна випадкова величина X прийме значення з інтервалу (а; b), можна знайти за формулою:
Теорема 2. Якщо неперервна випадкова величина приймає значення на відрізку [a,b] та має щільність ймовірності f(x), то її математичне сподівання знаходиться за формулою:
.
Дисперсію обчислюють за формулою:
Наслідок. Якщо диференціальна функція розподілу відома f(x), то інтегральну функцію розподілу F(x) можна знайти за формулою:
.
Розв’язок типових задач
Приклад 12.1. Знайти числові характеристики випадкової величини X, яка задана функцією розподілу:
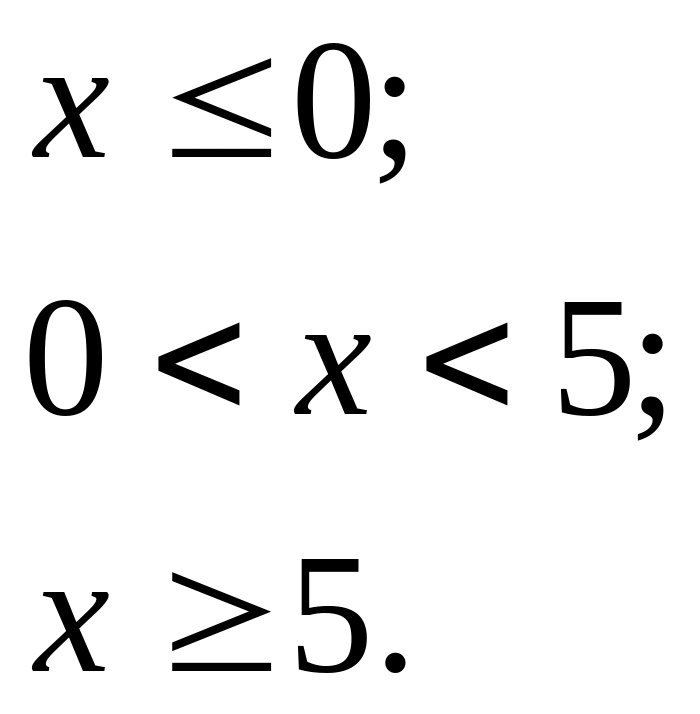
Розв'язання.
Спочатку знайдемо диференціальну
функцію розподілу, тобто щільність
ймовірності
:
Тепер за теоремою2 знаходимо математичне сподівання:
Далі знаходимо дисперсію:
Середнє квадратичне відхилення:
Приклад 12.2. Щільність ймовірності випадкової величини X має такий вигляд:
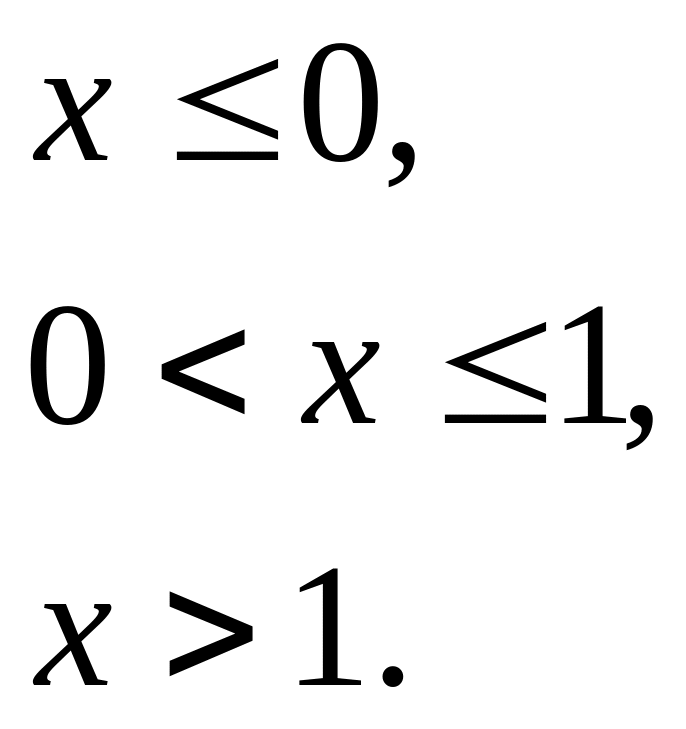
Знайти ймовірність того, що в результаті випробування X прийме значення, яке належить інтервалу (0,5; 1).
Розв'язання. Шукана ймовірність за теоремою 1 дорівнює:
Задачі
12.1. Випадкова величина X задана функцією розподілу:
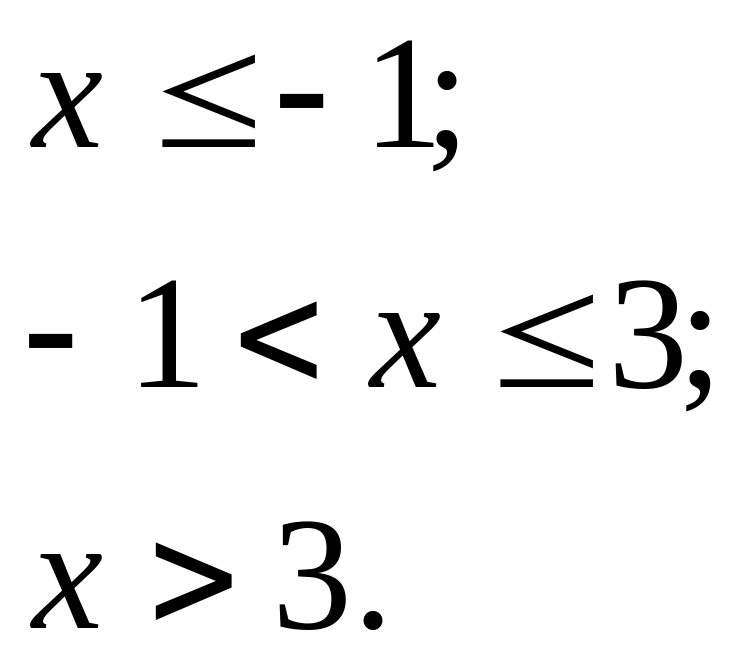
Знайти ймовірність того, що в результаті випробування X прийме значення, яке належить інтервалу (0, 2).
12.2. Випадкова величина X задана функцією розподілу:
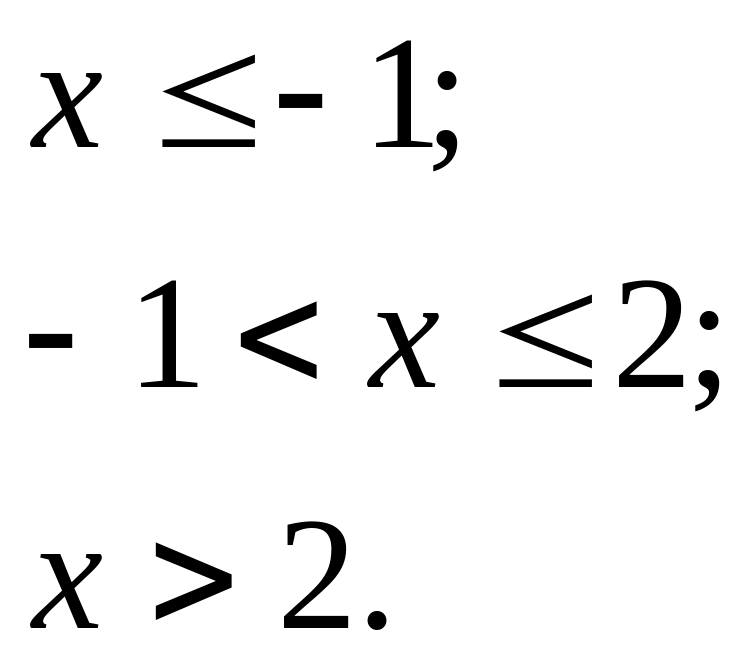
Знайти ймовірність того, що в результаті випробування X прийме значення, яке належить інтервалу (0; 1).
12.3. Випадкова величина X задана функцією розподілу:
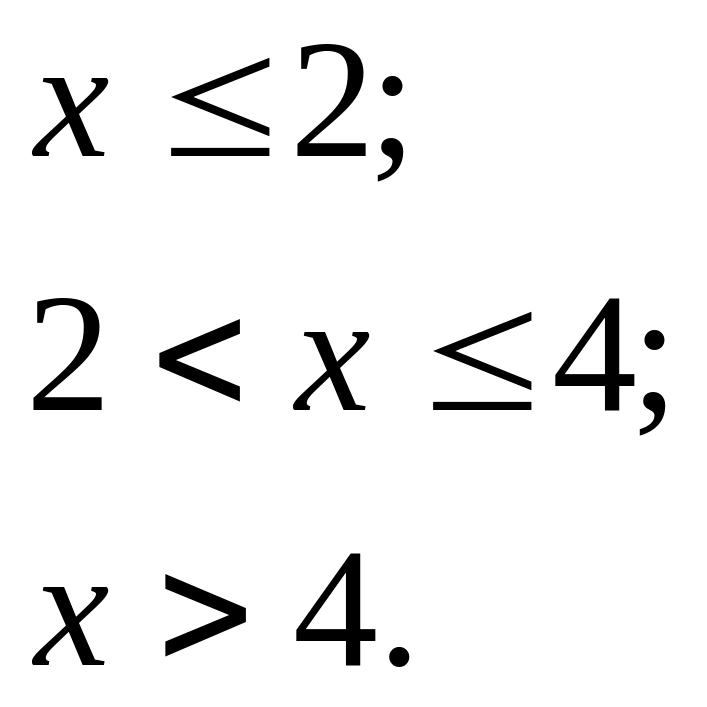
Знайти ймовірність того, що в результаті випробування X прийме значення, яке належить інтервалу (2; 3).
12.4. Задана щільність ймовірності випадкової величини X:
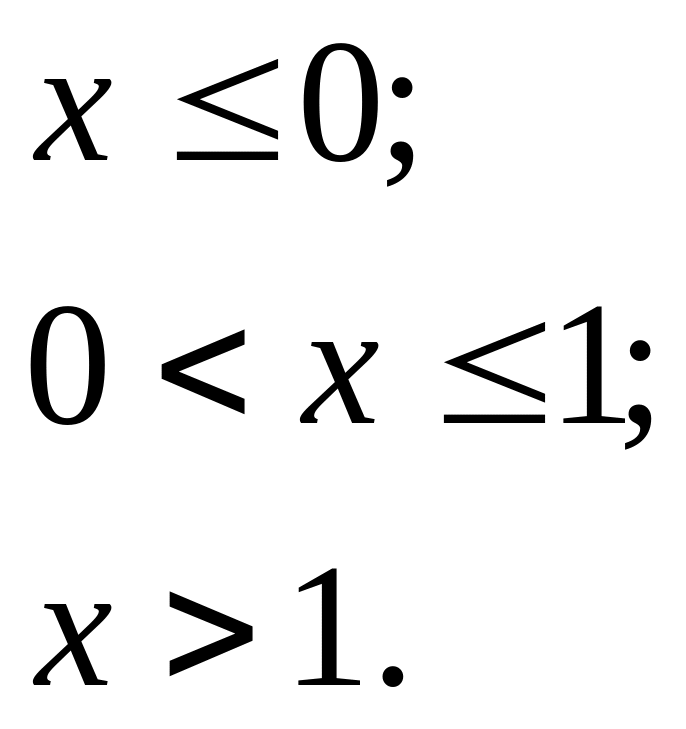
Знайти ймовірність того, що в результаті випробування X прийме значення, яке належить інтервалу (0,5; 1).
12.5. Знайти функцію розподілу за даною щільністю розподілу:
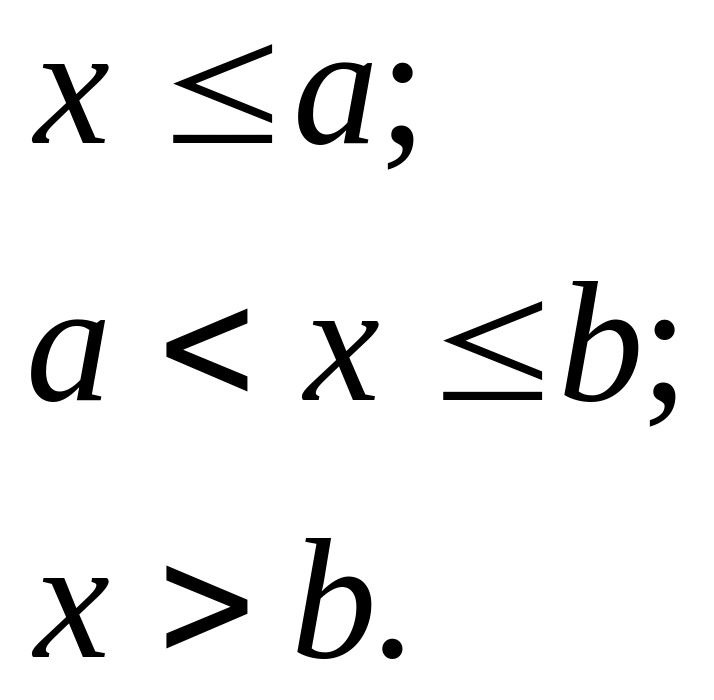
12.6. Закон розподілу неперервної випадкової величини X такий:
Знайти f(x) і обчислити P(0<X<2).
12.7. Щільність неперервної випадкової величини X подано у вигляді:
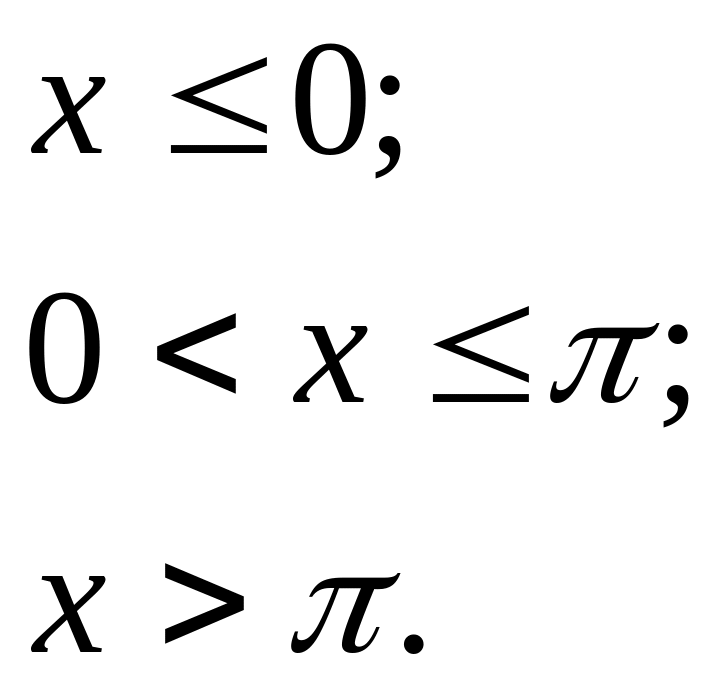
Знайти F(x)
та обчислити
.
12.8. Дано функцію розподілу ймовірностей:
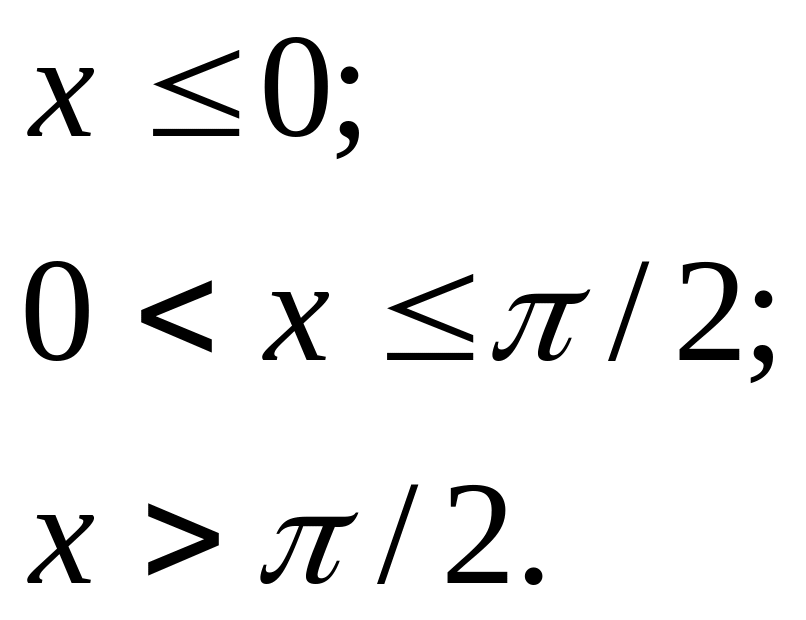
Знайти
f(x)
та обчислити
.
12.9. Дано функцію розподілу ймовірностей:
.
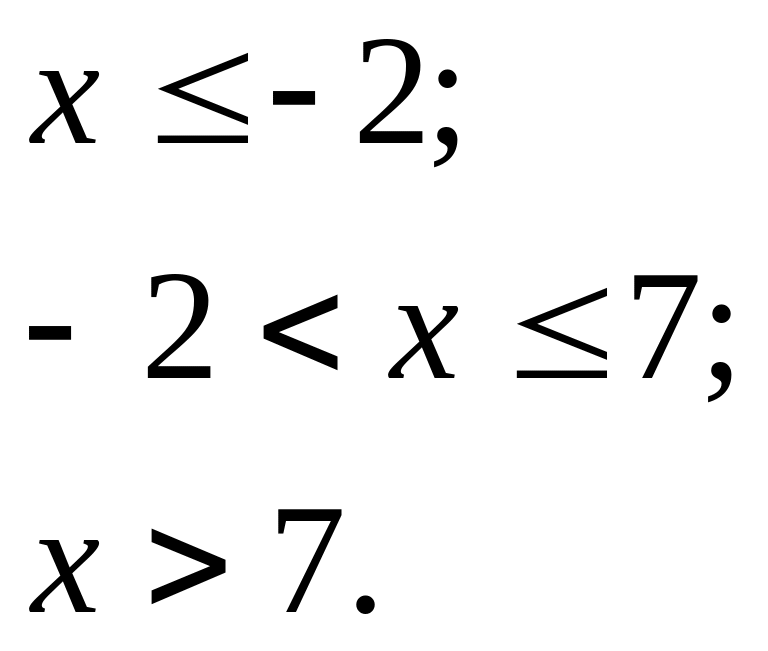Знайти f(x).
12.10. Знайти числові характеристики випадкової величини X, яка задана функцією розподілу:
12.11. Щільність ймовірності неперервної випадкової величини X подано у вигляді:
Знайти ймовірність
того, що X прийме значення
із проміжку
.
12.12. Задана диференціальна функція розподілу неперервної випадкової величини X:
Знайти інтегральну функцію розподілу.
12.13. Задана диференціальна функція розподілу неперервної випадкової величини X:
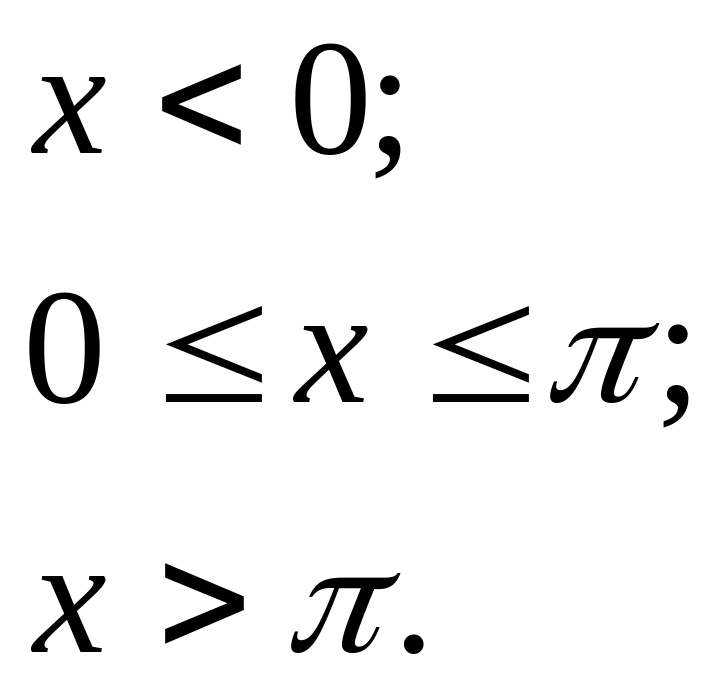
Знайти числові характеристики випадкової величини X.
12.14. Випадкова величина доходу X підприємства має диференціальну функцію розподілу:
Знайти M(X),
D(X) та ймовірність одержання прибутку
1; 5.
12.15. Диференціальна функція розподілу прибутку X підприємства відома:
(0; 5);
(0; 5).
Знайти математичне
сподівання прибутку, дисперсію та
ймовірність одержання прибутку
млн. грн.
12.16. Знайти дисперсію та середнє квадратичне відхилення випадкової величини X, яка задана функцією розподілу:
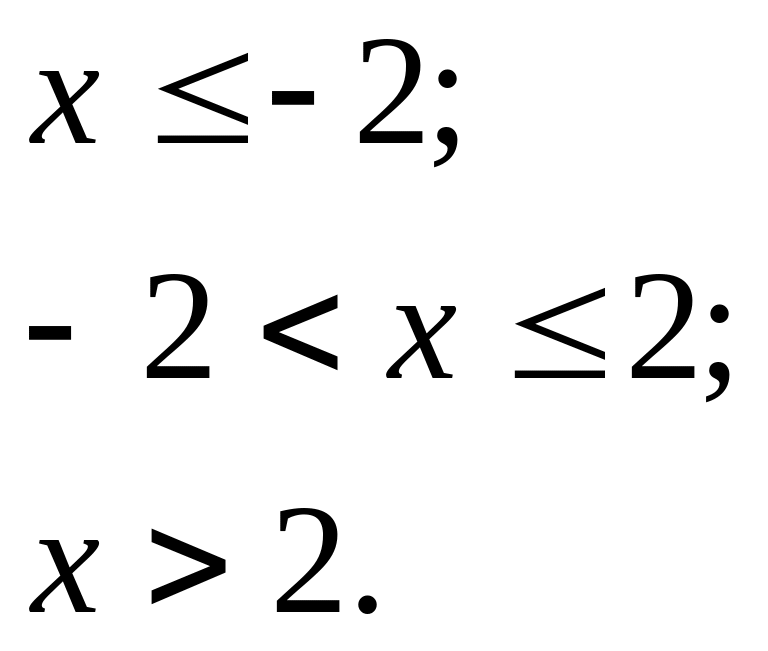
Неперервна випадкова величина X розподілена за показниковим законом розподілу:
.
Знайти ймовірність того, що в результаті випробування X прийме значення, яке належить інтервалу (1; 3).
12.18. Обчислити дисперсію випадкової величини, що розподілена рівномірно:
(a;
b)
(a;
b).
Знайти математичне сподівання та дисперсію випадкової величини X, що має таку густину розподілу:
Густина розподілу ймовірності випадкової величини X має такий вигляд:
Знайти математичне сподівання та дисперсію.
Щільність розподілу випадкової величини X дорівнює:
.
Знайти функцію розподілу та математичне сподівання.
Щільність розподілу випадкової величини X дорівнює:
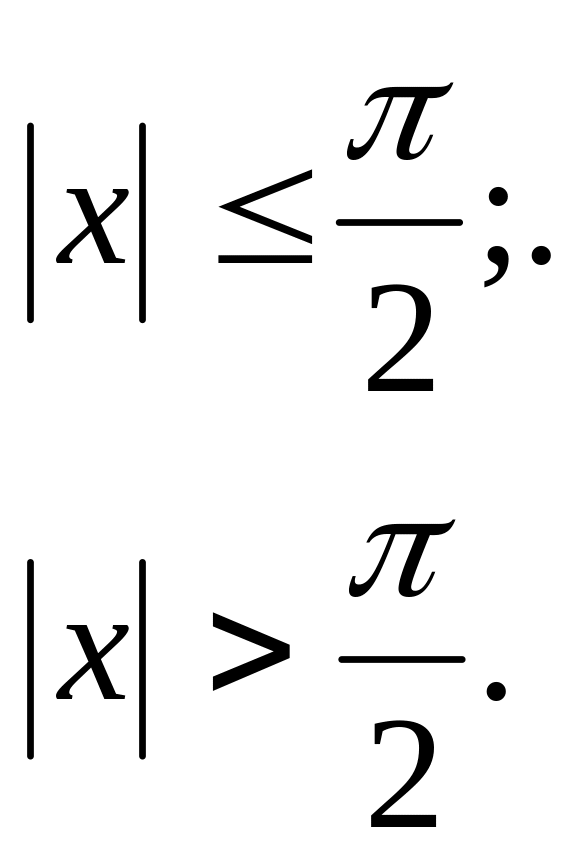
Знайти математичне сподівання та дисперсію випадкової величини.