Смешанное произведение трех векторов.

Определение: Смешанным произведением трех векторов , , называется число, равное векторному произведению , умноженному скалярно на вектор .

Обозначение смешанного произведения

В результате смешанного произведения трех векторов получается число .

Если , то тройка векторов , , - правая.

Если , то тройка векторов , , - левая.

Определение: Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю, т. е.  векторы , , - компланарны.

Свойства смешанного произведения

1. Смешанное произведение не изменится при круговой перестановке векторов .

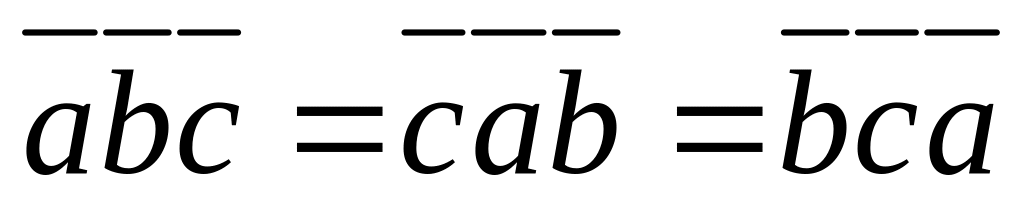2. Перестановка двух соседних сомножителей меняет знак произведения на противоположный .

3. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения .

4. Смешанное произведение ненулевых векторов , , равно нулю тогда и только тогда, когда они компланарны.

Выражение смешанного произведения через координаты

Пусть заданы векторы , , . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

.

Полученную формулу можно записать короче: 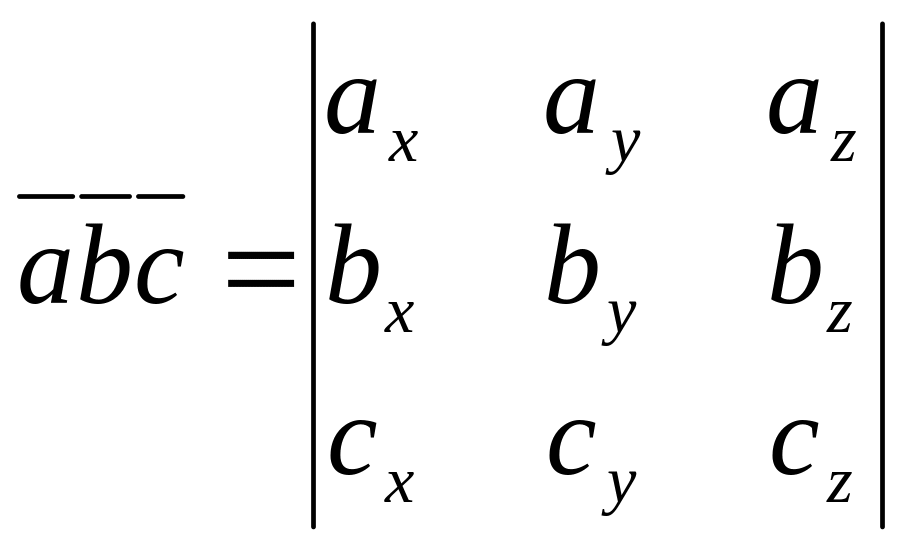, так как правая часть представляет собой разложение определителя третьего порядка по элементам третьей строки.

Определение: Смешанное произведение векторов, заданных своими координатами, равно определителю третьего порядка, составленному из координат перемножаемых векторов.

Приложения смешанного произведения

Определение объемов параллелепипеда и треугольной пирамиды

Объем параллелепипеда, построенного на векторах , и вычисляется как , т. е. абсолютная величина смешанного произведения равна объему параллелепипеда, построенного на векторах , и .

Объем треугольной пирамиды

.

Замечание1.

Знак перед определителем должен быть выбран так, чтобы объем V был положительным.

Замечание 2.

Предполагается, что векторы , и не лежат в одной плоскости (некомпланарны).

Задачи.

Задача 1. Вектор перпендикулярен к векторам и , угол между и равен . Зная, что , , , вычислить .

Решение:

Рис. 1 Рис. 2

По условию задачи тройка векторов , , может быть правой (Рис. 1) или левой (Рис. 2).

, где , .

По условию задачи .

Угол (Рис. 1), (Рис. 2), следовательно, . Тогда .

Задача 2. Даны координаты вершин пирамиды , , и . Определить ее объем.

Решение:

Рис. 3

Рассмотрим три вектора: , , . Найдем объем пирамиды по формуле (9)

В правой части выбран знак минус, так как определитель отрицателен.

Задача 4. Показать, что точки , , и лежат в одной плоскости.

Решение:

Р ассмотрим три вектора , и .

Находим смешанное произведение векторов:

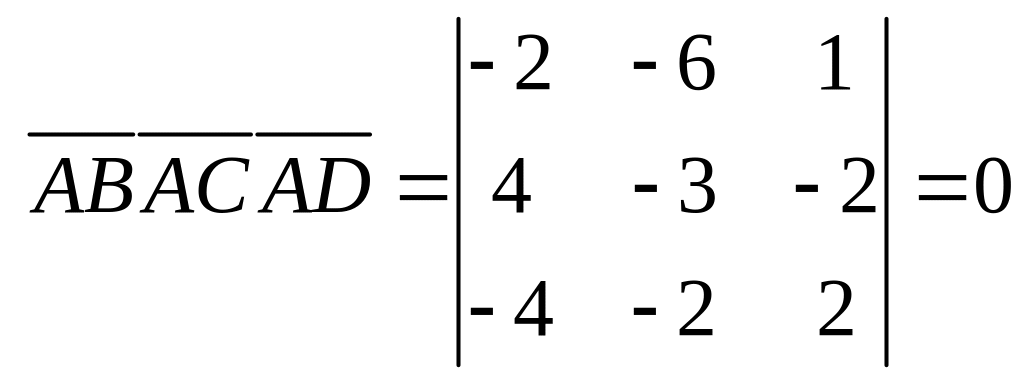(Элементы первого и третьего столбцов пропорциональны).

Поскольку , то векторы компланарны, т. е. точки A, B, C, D лежат в одной плоскости.