Линейные операции над векторами.

Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.

Пусть и - два произвольных вектора. Возьмем произвольную точку О и построим вектор ; затем от точки А отложим вектор . Вектор , соединяющий начало первого слагаемого вектора с концом второго называется суммой этих векторов и и обозначается . (Рис. 1)

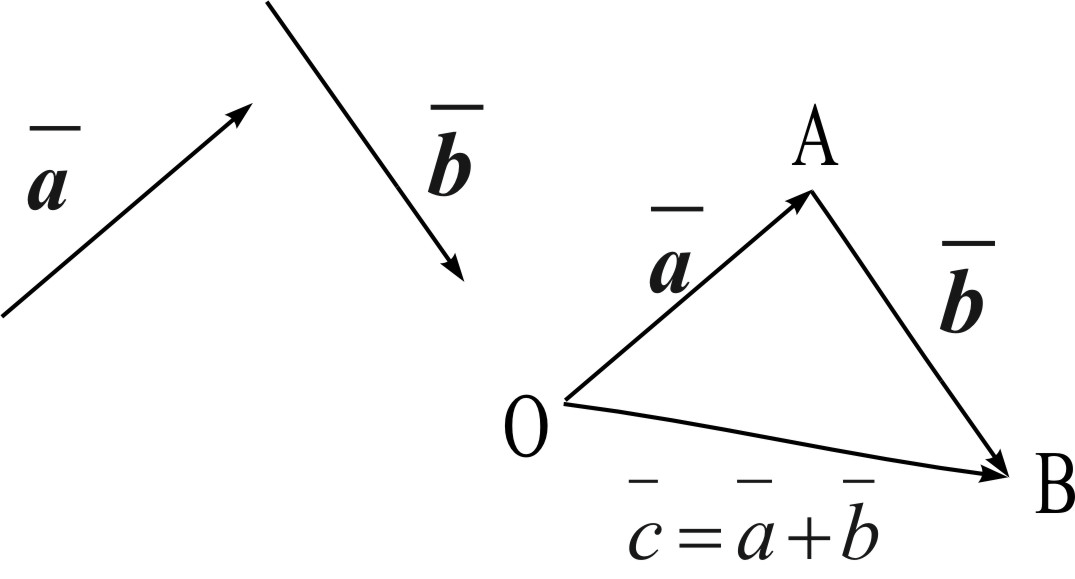
Рис. 1

Это правило сложения векторов называют правилом треугольника.

Сумму двух векторов можно построить также по правилу параллелограмма. Отложим от точки О векторы и . Построим на этих векторах как на сторонах параллелограмм OACB. Вектор , служащий диагональю параллелограмма, проведенной из вершины О, является суммой векторов . (Рис. 2)

Рис. 2

Модуль вектора вычисляется по формуле

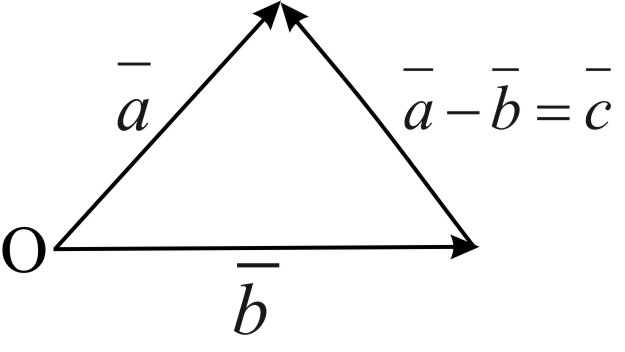
Разностью двух векторов и называется третий вектор , сумма которого с вычитаемым вектором дает вектор , т. е. . (Рис. 3)

Если на векторах и , отложенных из общей точки О, построить параллелограмм, то вектор , совпадающий с одной диагональю параллелограмма, исходящей из точки О, равен сумме , а вектор , совпадающий с другой диагональю равен разности . (Рис. 4).

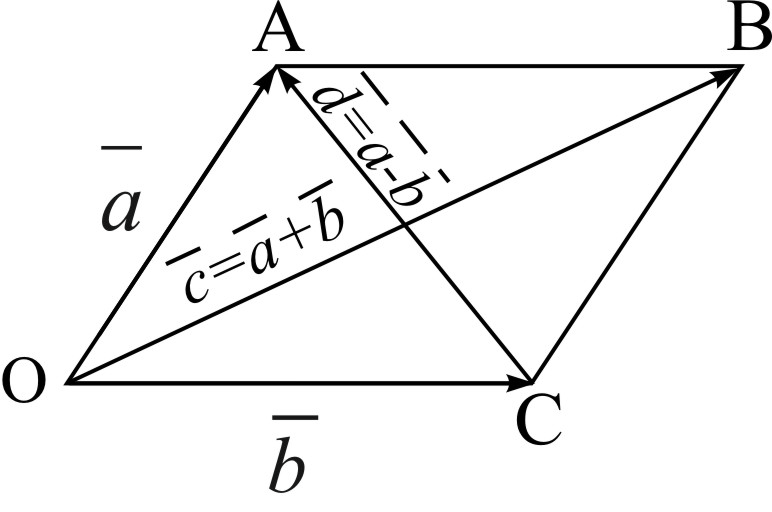
Рис. 4

Модуль вектора вычисляется по формуле

При умножении вектора на скаляр (число)  получается вектор : .

Полученный вектор удовлетворяет следующим условиям:

1. 

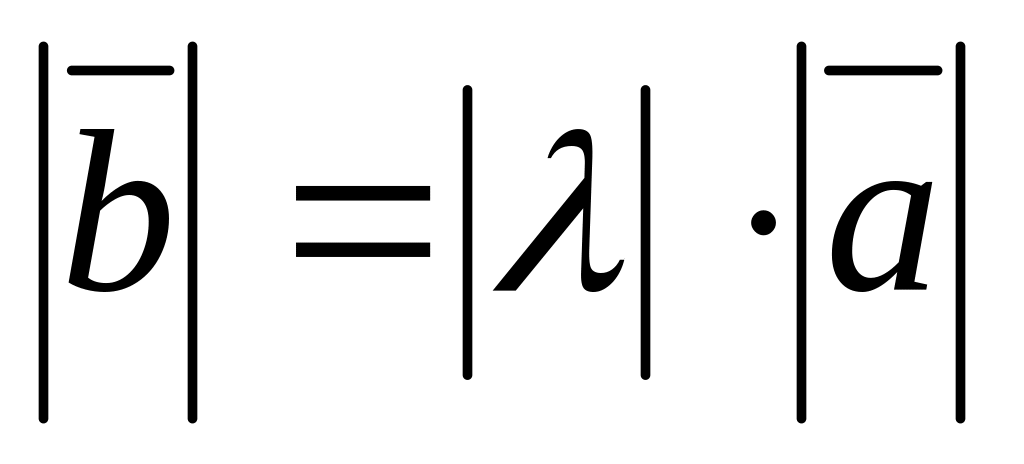
2. вектор коллинеарен вектору

3. , если  > 0

4. , если  < 0

Замечание.

Т. к. вектор коллинеарен вектору , то в дальнейшем условие коллинеарности векторов будем записывать в виде .

При умножении вектора на скаляр (число)  получается вектор :

Действия над векторами, заданными проекциями.

Определение: Тройка векторов , , называется координатным базисом, если эти векторы удовлетворяют условиям:

1. вектор лежит на оси OX, вектор - на оси OY, вектор - на оси OZ.

2. каждый из векторов , , направлен на своей оси в положительную сторону.

3. векторы , , - единичные, т. е.

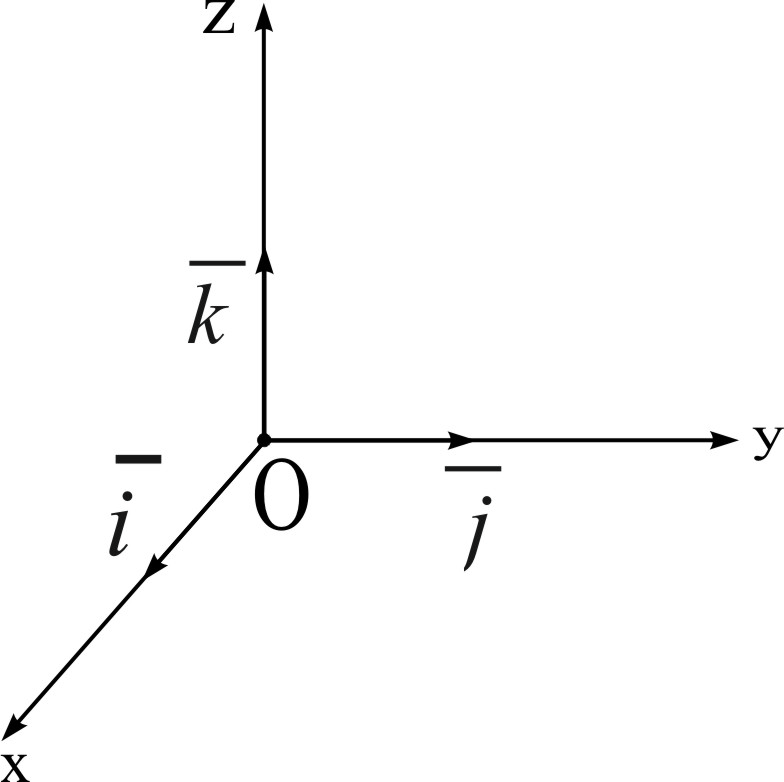
Рис. 1

Каким бы ни был вектор , он всегда может быть разложен по базису , , , т. е. может быть представлен в виде , где , , - проекции вектора на координатные оси (координаты вектора).

При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).

или

или

или (2)

При умножении вектора на скаляр координаты вектора умножаются на этот скаляр.

или

Признаком коллинеарности двух векторов и является пропорциональность их координат: .

Задачи

Задача 1. Найти сумму и разность векторов .

Решение: По формуле имеем

или

или .

Задача 2. Проверить коллинеарность векторов и , где , . Установить, какой из них длиннее другого, во сколько раз, как они направлены: в одну или противоположные стороны.

Решение: По формулам находим векторы и в координатной форме.

, ,

, ,

, т. к. , .

Вектор длиннее вектора в три раза. Векторы и направлены в противоположные стороны ( ), т. к. .