II. Векторная алгебра

Лекция № 6. Понятие вектора. Проекции вектора.

Определение: Вектор – это направленный отрезок прямой. Вектор обозначается обычно двумя буквами, сначала пишется буква, указывающая начало, а потом, буква, указывающая конец вектора. Вектор обозначается или .

Рис. 1

Определение: Длина вектора называется его модулем и обозначается символом или .

Определение: Вектор, длина которого равна нулю, называется нулевым вектором. Нулевой вектор направления не имеет. Обозначается - нулевой вектор.

Определение: Вектор, длина которого равна единице, называется единичным вектором и обозначается - единичный вектор

Определение: Векторы, расположенные на одной прямой или параллельных прямых, называются коллинеарными. (Рис. 3)

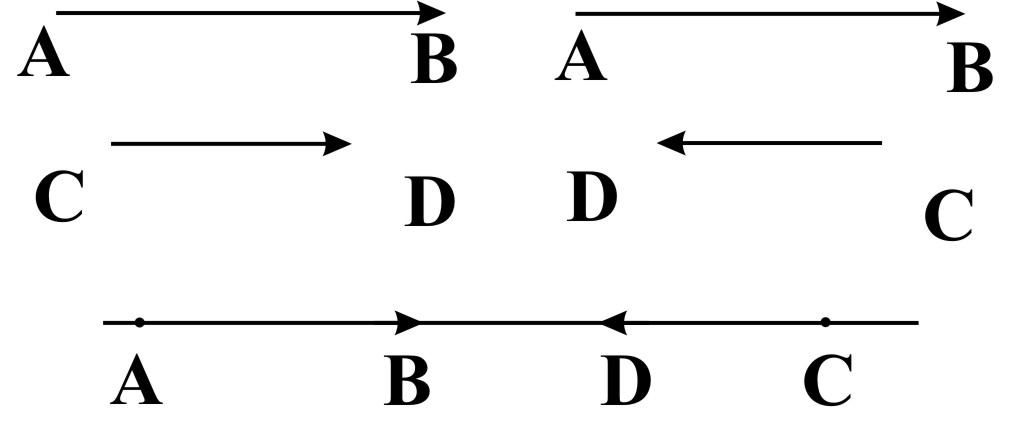
Рис. 2

Определение: Два вектора называются равными, если они:

1. имеют равные модули

2. коллинеарны

3. направлены в одну сторону (Рис. 3)

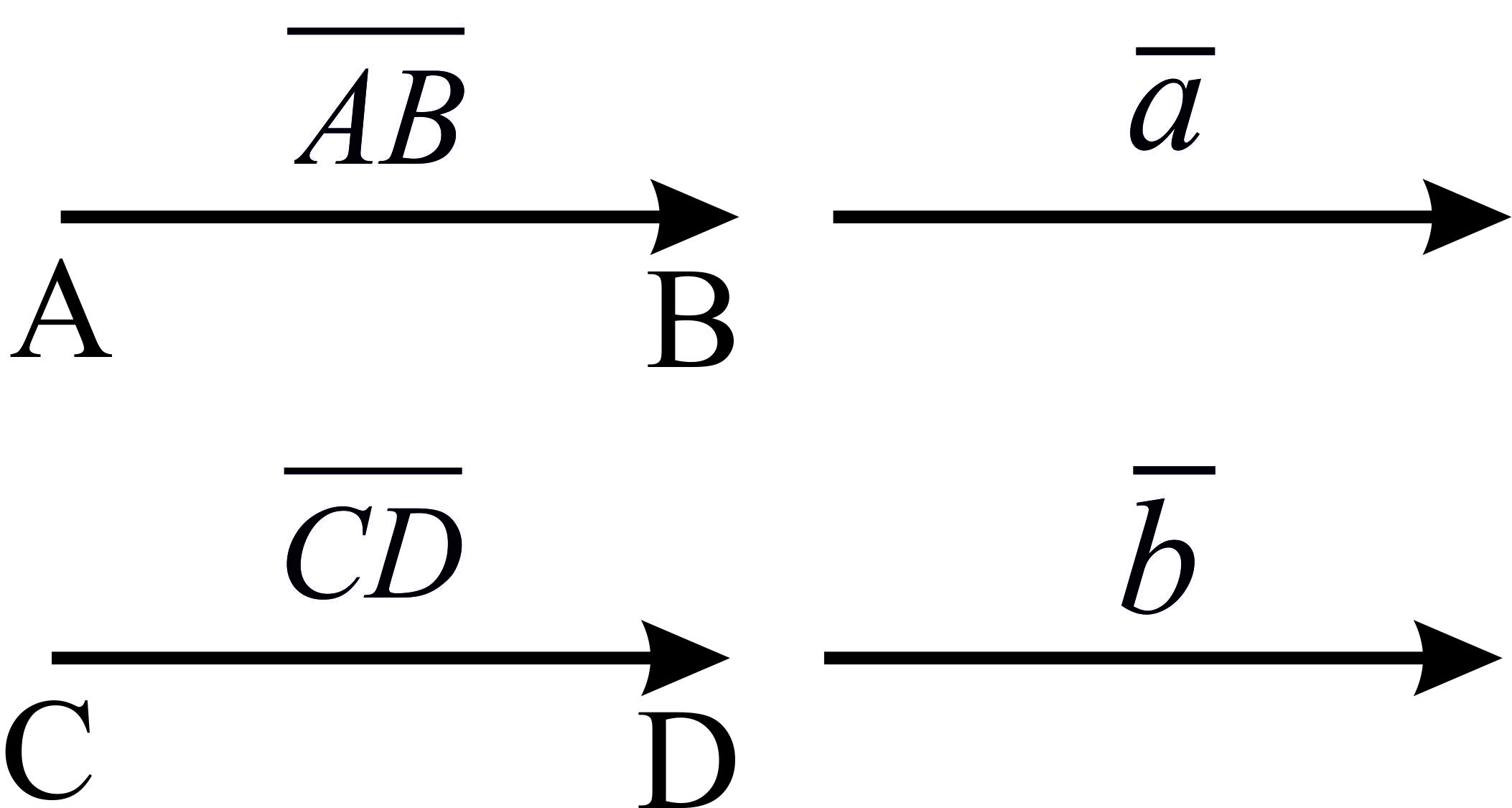
Рис. 3

или

Определение: Вектора называются противоположными, если они:

1. Имеют равные модули

2. коллинеарны

3. направлены в противоположную сторону(Рис. 4)

и - противоположные векторы или и

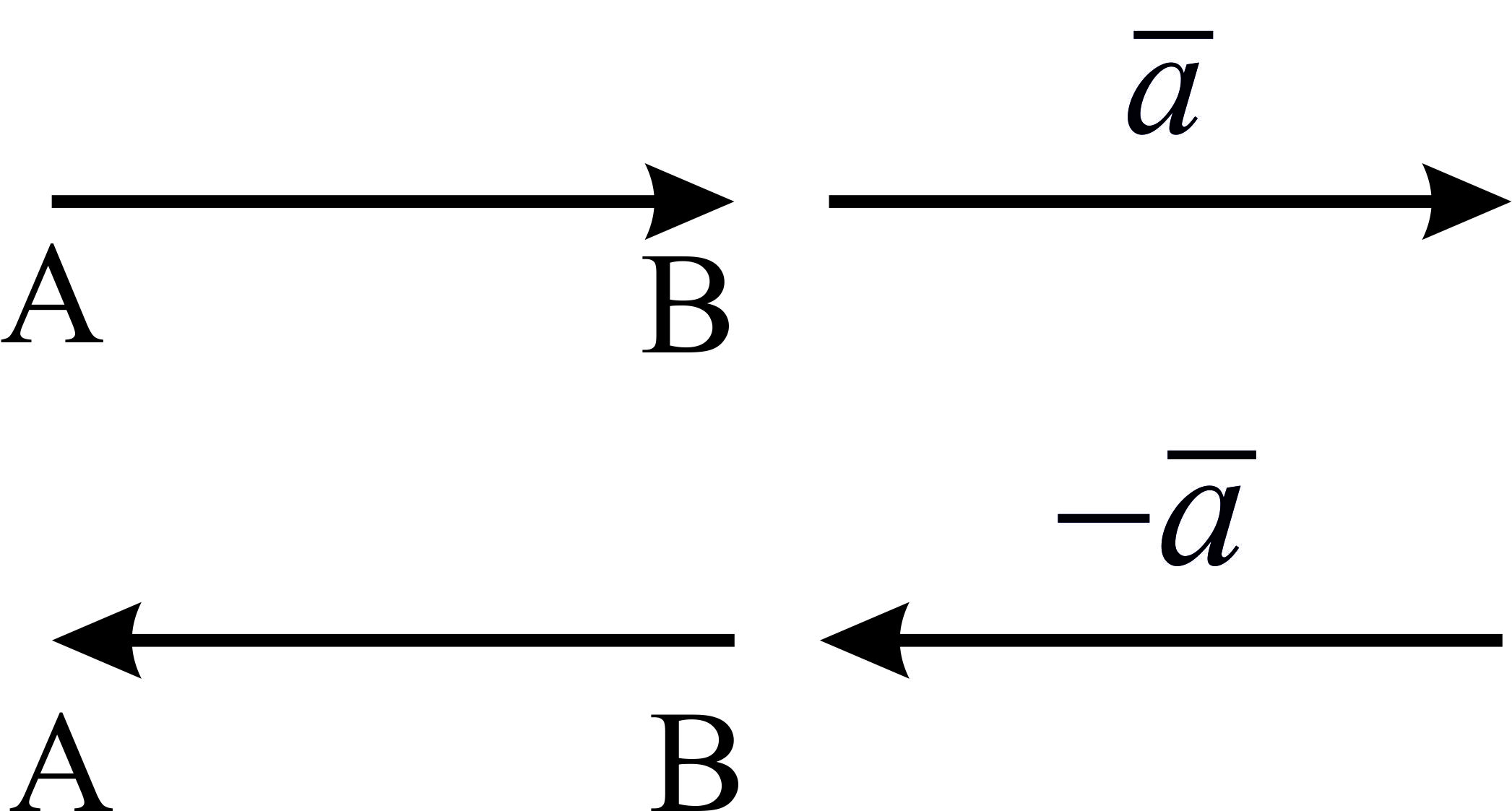
Рис. 4

Определение: Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или параллельны некоторой плоскости. (Рис. 5)

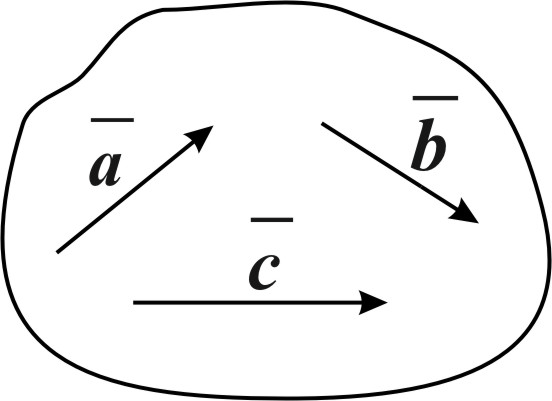
Рис. 5

Определение: Проекцией вектора на ось l, называется длина отрезка , заключенного между проекциями начала и конца вектора на эту ось. Эта длина берется со знаком плюс, если направление отрезка совпадает с направлением оси, и со знаком минус, если его направление противоположно направлению оси.

Проекция вектора на ось положительна, если вектор образует с осью острый угол и отрицательна, если вектор образует с осью тупой угол. (Рис. 6)

Рис. 6

Проекции вектора на координатные оси называют также его (декартовыми) координатами.

Координаты вектора равны разностям соответствующих координат его конца и начала.

Если для вектора известны координаты его начала и координаты его конца , то проекции вектора на оси координат определяются по формулам

б

Модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.

Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле:

Если вектор исходит из начала координат, а его конец М имеет координаты , то тогда его проекции на координатные оси равны координатам его конца: .

Определение: Радиус – вектор точки обозначается через . Модуль радиус - вектора точки вычисляется по формуле

- называют направляющими косинусами вектора .

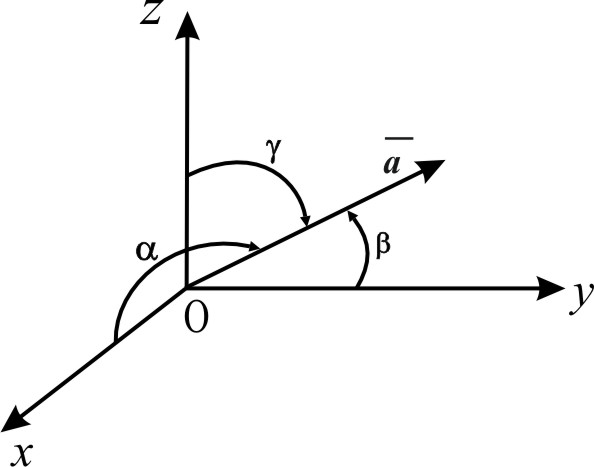
Рис. 7

Если , ,  - углы, образованные вектором с координатными осями OX, OY, OZ прямоугольной системы координат, то проекции вектора на координатные оси будут равны

Сумма квадратов направляющих косинусов ненулевого вектора равна единице . Данное равенство позволяет определить один из углов , ,  , если известны два других.

Координатами единичного вектора являются числа , т. е.

Задачи

Задача 1. Вектор задан координатами своих концов А и В: ; . Найти проекции вектора на координатные оси и его направляющие косинусы.

Решение: Проекции вектора на координатные оси находим по формулам (4):

, , .

Длина вектора определяется по формуле: .

Направляющие косинусы: ; ; .

Задача 2. Дан модуль вектора и его углы с осями координат: , а  - тупой угол. Вычислить проекции этого вектора на координатной оси.

Решение: Используем формулу (9) для определения .

Так как  - тупой угол, следовательно, . Проекции вектора на оси координат находим по формулам (8):

.
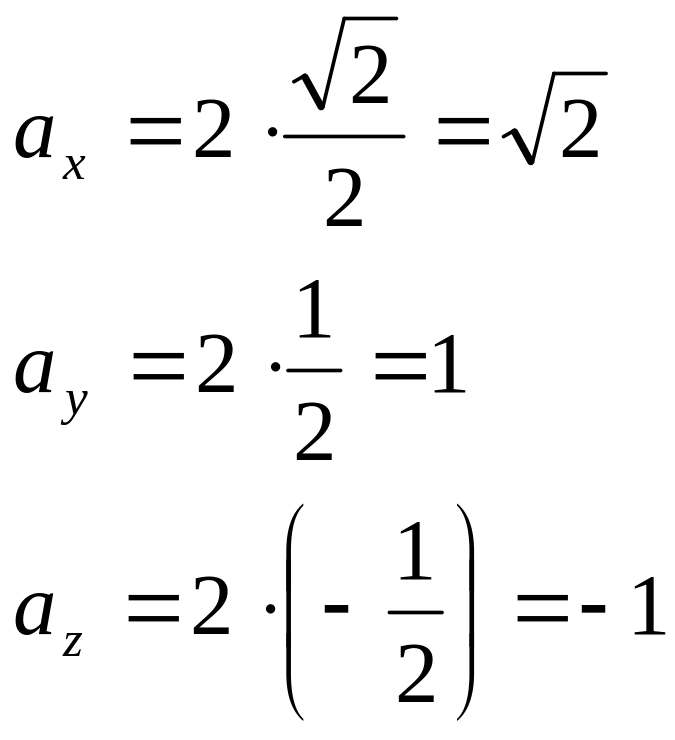