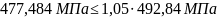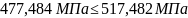- •1. Выбор электродвигателя и кинематический расчёт привода
- •2. Расчет открытой ремённой передачи
- •3. Расчет зубчатой передачи
- •4. Определение диаметров валов по приближенным зависимостям
- •5. Расчёт шпоночных соединений
- •6. Первый этап компоновки редуктора
- •7. Составление расчётных схем валов. Определение опорных реакций. Построение эпюр изгибающих и крутящих моментов.
- •8. Расчет валов на выносливость
- •9. Расчет подшипников качения на грузоподъемность.
- •9. Конструктивные размеры корпуса редуктора
- •Список литературы:
Министерство Транспорта Российской Федерации
Федеральное агентство морского и речного транспорта
Московская Государственная Академия Водного Транспорта

Кафедра ППТМ и Р
Курсовой проект
«Проектирование редуктора»
по дисциплине
«Детали Машин»
Выполнил(а): |
|
|
|
Проверил(а): |
|
Москва
2011
1. Выбор электродвигателя и кинематический расчёт привода
1.1. Подбор электродвигателя:
По таблице 1.1 ([1], с.7) примем:
–
КПД пары подшипников
качения,
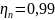 ;
;
–
КПД муфты:
 ;
;
–
КПД цилиндрической
передачи:
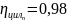 ;
;
–
КПД ременной
передачи:
 ;
;
Из задания видно, что в схеме применяется: 1 муфта, 3 пары подшипников, 1 цилиндрическая передача, 1 ременная передача. Отсюда:
Общий КПД привода:
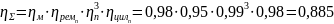
Частота вращения выходного вала:
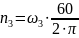
Где,
 – угловая скорость
3-его (выходного) вала, рад/сек.
– угловая скорость
3-его (выходного) вала, рад/сек.
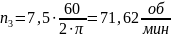
Частота вращения вала электродвигателя:


Требуемая мощность электродвигателя:
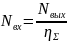
Где,
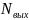 – потребляемая
мощность привода, кВт.
– потребляемая
мощность привода, кВт.

По
таблице 19.28 ([1], с.510) принимаем
электродвигатель 90L6/925,
для которого
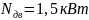 ,
,
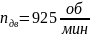 .
.
1.2. Определение передаточных чисел:
Общее передаточное число привода:
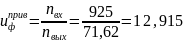
Передаточное число открытой передачи:
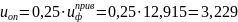
Передаточное число редуктора:
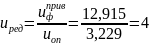
Из стандартного ряда ([1], с.481) принимаем:
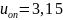
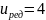
Погрешность:
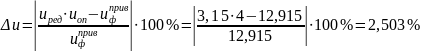
Что вполне приемлемо, т.к. не превышает 5%
1.3. Определение вращающих моментов на валах:
Частоты вращения на валах:
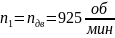
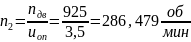
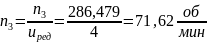
Моменты на валах:
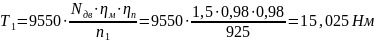
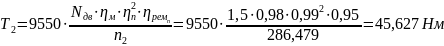
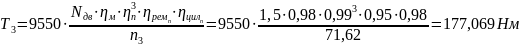
2. Расчет открытой ремённой передачи
Подбираем
плоский ремень с параметрами с толщиной
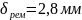 .
.
Диаметр малого шкива:
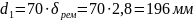
Принимаем
стандартный
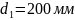 .
.
Скорость ремня:
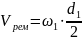
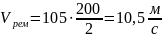
Расчетный диаметр большого шкива:
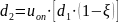
Где,
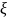 – коэффициент
скольжения (
– коэффициент
скольжения (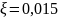 ).
).
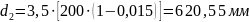
Из
стандартного ряда принимаем
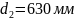
Фактическое передаточное число:
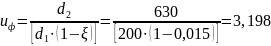
Ориентировочное межосевое расстояние:
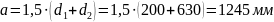
Расчетная длина ремня:
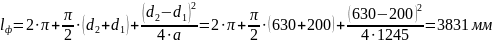
Из
стандартного ряда принимаем
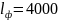
Частота пробегов:

Фактическое межосевое расстояние:
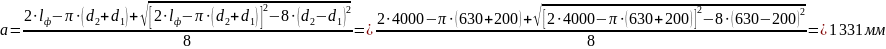
Угол обхвата:
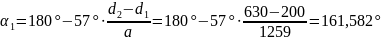
Из
стандартного ряда принимаем
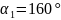
Окружная сила:
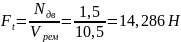
Подбор поправочных коэффициентов:
Коэффициент
угла наклона:
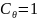 ;
;
Для
плоскоременных передач с углом обхвата
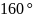 :
:
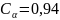 ;
;
Коэффициент
влияния диаметра меньшего шкива:
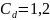 ;
;
Коэффициент
неравномерности распределения нагрузки:
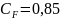 ;
;
Коэффициент
влияния центробежной силы:
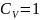 ;
;
Коэффициент
динамичности для спокойного типа работы
при односменной нагрузке:
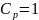 ;
;
Допускаемая
приведенная сила в ремне:
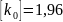 .
.
Допускаемая мощность, передаваемая одним ремнем:
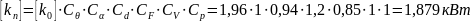
Ширина ремня:
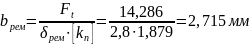
Из
стандартного ряда принимаем
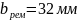 .
.
Сила предварительного натяжения:
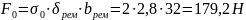
Сила, действующая на валы:

3. Расчет зубчатой передачи
3.1. Выбор материала колеса и шестерен и термической обработки
Так как в задание нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками. По таблице 2.1 ([1] ,с.17) принимаем для шестерни и для колеса Сталь 40Х (0,4% углерод, 1% хрома), термообработка – улучшение.
Таблица №1 Параметры материала
Марка стали |
Термообработка |
Предельные размеры заготовки, мм |
Твердость зубьев |
σТ, H/мм2 |
|||
Dпр |
Sпр |
в сердцевине |
на поверхности |
||||
40Х |
Улучшение |
200 |
125 |
235…262HB |
235…262HB |
640 |
|
125 |
80 |
269…302HB |
269…302HB |
750 |
|||
3.2. Определяем среднюю твердость рабочих поверхностей зубьев.
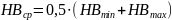
Для
колеса –
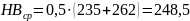
Для
шестерни –
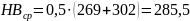
3.3. Определяем базовое число циклов нагружений
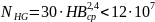 – при расчете на
контактную прочность;
– при расчете на
контактную прочность;
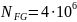 – при расчете на
изгиб.
– при расчете на
изгиб.
Для
колеса –
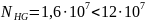
Для
шестерни –
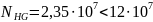
3.4. Определяем действительные числа циклов перемены напряжений
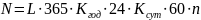
Где,
 – срок службы (
– срок службы ( );
);
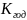 – коэффициент
годового использования передачи;
– коэффициент
годового использования передачи;
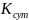 – коэффициент
суточного использования передачи.
– коэффициент
суточного использования передачи.
Для
колеса –
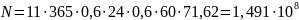
Отсюда –
Коэффициент долговечности при расчете на контактные напряжения:
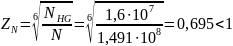 ,
принимаем
,
принимаем
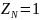
Коэффициент долговечности при расчете на изгиб:
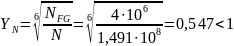 ,
принимаем
,
принимаем
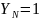
Для
шестерни –
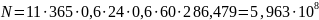
Отсюда –
Коэффициент долговечности при расчете на контактные напряжения:
 ,
принимаем
,
принимаем
Коэффициент долговечности при расчете на изгиб:
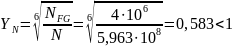 ,
принимаем
,
принимаем
3.5. Определяем пределы контактной и изгибной выносливости
 – контактная
выносливость,
– контактная
выносливость,
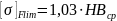 – изгибная
выносливость.
– изгибная
выносливость.
Для колеса:
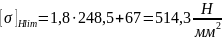
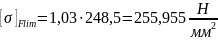
Для шестерни:
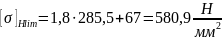
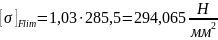
Допускаемое
контактное напряжение для прямозубой
передачи это меньшее из
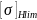 :
:
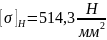
3.6. Межосевое расстояние
Принимаем
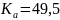 ,
коэффициент межосевого расстояния для
прямозубой цилиндрической передачи.
Коэффициент ширины,
,
коэффициент межосевого расстояния для
прямозубой цилиндрической передачи.
Коэффициент ширины,
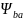 принимаем 0,315 т.к. передача располагается
симметрично.
принимаем 0,315 т.к. передача располагается
симметрично.
Коэффициент
ширины,
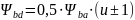 т.к. передача внешнего зацепления, то
т.к. передача внешнего зацепления, то
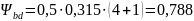
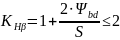 ,
по таблице ([1], с.21) выбираем
,
по таблице ([1], с.21) выбираем
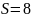 ,
т.к. передача симметрична.
,
т.к. передача симметрична.
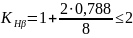
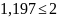
Т.к.
термообработка колес произведена по I
варианту (улучшение) и скорость колеса
не достигает
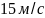 ,
то
,
то
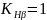 .
([1], с.20)
.
([1], с.20)
Межосевое расстояние

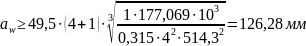
По
таблице 19.28 ([1] ,с.481) принимаем
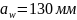
3.7. Модуль передачи
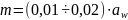
Из
конструктивных соображений принимаем
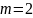
3.8. Предварительные основные размеры колеса
–
делительный диаметр
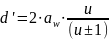 ,
передача внешнего зацепления, поэтому
,
передача внешнего зацепления, поэтому
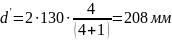
–
ширина
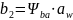
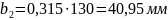
3.9. Угол наклона и суммарное число зубьев
Так
как передача прямозубая угол наклона
зубьев равен
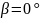
Отсюда
суммарное число зубьев равно
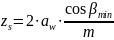 ,
,
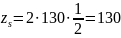
Принимаем
число зубьев
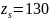
3.10. Числа зубьев шестерни и колеса
Во
избежание подреза, минимально допустимое
число зубьев –

Число
зубьев шестерни –
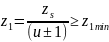
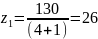
Принимаем
 ,
что больше минимального числа зубьев
(
,
что больше минимального числа зубьев
(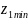 ).
).
Число
зубьев колеса внешнего зацепления
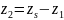
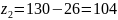
3.11. Фактическое передаточное число
Вычислим
его по формуле
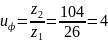 ,
рассчитаем отклонение от заданного
передаточного числа,
,
рассчитаем отклонение от заданного
передаточного числа,
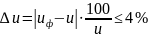 вычисляем
вычисляем
 ,
получаем погрешность в пределах
допустимого
,
получаем погрешность в пределах
допустимого
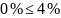 .
.
3.12. Размеры колес
Делительные диаметры:
–
шестерни

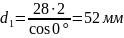
–
колеса внешнего
зацепления
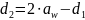
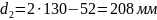
Диаметры окружностей вершин и впадин зубьев:
–
диаметр вершин
шестерни

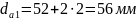
–
диаметр впадин
шестерни
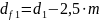
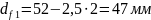
–
диаметр вершин
колеса

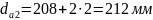
–
диаметр впадин
шестерни
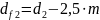
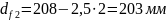
Ширину
шестерни принимают по соотношениям
([1], с.24) при
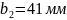 ,
соотношение
,
соотношение
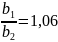 ,
отсюда
,
отсюда
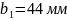
3.13. Пригодность заготовок колес
Условие пригодности колес:
–
для цилиндрической
шестерни
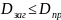 ,
,
 ;
;
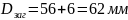
–
для колеса с
выточками
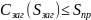 ,
,
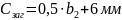 ;
;
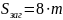 .
.
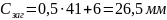
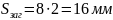
Параметры материала взяты по таблице 2.1 ([1], с.17).
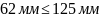
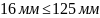
Проверка прошла.
3.14. Силы в зацеплении
–
окружная
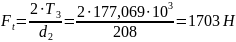 ;
;
–
радиальная
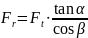 т.к. угол профиля стандартный берем
т.к. угол профиля стандартный берем
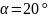 ,
,
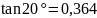 соответственно
соответственно
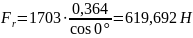 ;
;
3.15. Проверка зубьев по напряжениям изгиба
По
таблице 2.4 ([1], с.25) принимаем степень
точности передачи равной 8, Допустимая
скорость колеса, равняется
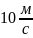 ,
соответственно. Сравниваем вычисленную
окружную скорость колеса с допустимой:
,
соответственно. Сравниваем вычисленную
окружную скорость колеса с допустимой:
–
окружная скорость
колеса
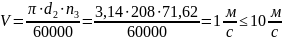 – проходит.
– проходит.
Передача
прямозубая, степень точности 8, так что
коэффициент
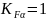
Коэффициент
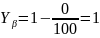
Коэффициент
ширины
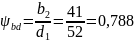
Коэффициент
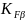 принимается исходя из твердости и
скорости колеса, при твердости менее
350HB
и окружной скорости
принимается исходя из твердости и
скорости колеса, при твердости менее
350HB
и окружной скорости
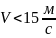 ,
,
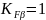
Коэффициент
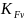 для прямозубых колес, твердость которых
меньше 350HB
принимается
для прямозубых колес, твердость которых
меньше 350HB
принимается
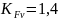
Коэффициент
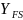 ,
учитывающий форму зуба и концентрацию
напряжений, зависит от приведенного
числа зубьев:
,
учитывающий форму зуба и концентрацию
напряжений, зависит от приведенного
числа зубьев:
По
таблице 2.5 ([1], с.26) принимаем
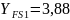 ,
,
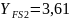 .
.
Расчетное напряжение изгиба в зубьях колеса
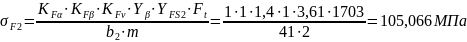
Расчетное напряжение изгиба в зубьях шестерни
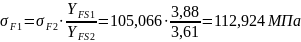
Напряжения проходят проверку:
Для шестерни:
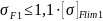
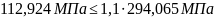
Для колеса:
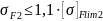
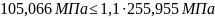
3.16. Проверка зубьев по контактным напряжениям
Коэффициент
распределения нагрузки между зубьями
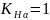 ,
т.к. передача прямозубая.
,
т.к. передача прямозубая.
Коэффициент
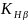 определен ранее и равен
определен ранее и равен
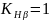 .
.
Коэффициент
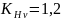 принимаем исходя из типа передачи и
твердости зубьев.
принимаем исходя из типа передачи и
твердости зубьев.
Расчетное контактное напряжение в зацеплении прямозубых передач
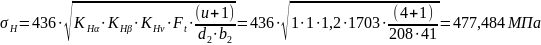
Напряжения проходят проверку: