Ответы, указания, решения

9 Класс

1. Ответ: достаточно нанести 4 деления: 1 см, 6 см, 9 см, 11 см.

Решение. Меньшим числом делений обойтись не удается, так как 5 точек (концы линейки и возможные 3 точки деления) определяют не более 10 различных отрезков, а нам требуется измерить 13 отрезков.

Легко убедиться, что четырех указанных делений достаточно. Так, например, отрезок в 2 см можно получить как расстояние от конца линейки до деления в 11 см. Остальные отрезки могут быть получены аналогично. Проверьте это самостоятельно.

2. Ответ: –1.

Решение. Запишем цепочку равенств:

, , , .

Аналогично: , .

Получаем = =–1.

3. Ответ: два корня.

Решение. Рассмотрим функцию f(x)=x²+px+q.

Поскольку f(–1)=1–(p–q)<0, а ветви параболы направлены вверх, то график функции у=f(x) пересекает ось абсцисс в двух точках, а, следовательно, данное уравнение имеет два корня.

4. Указание. В силу подобия треугольников ОВМ и ОDС и треугольников ОАВ и ОСР, получаем пропорции:

ОМ : ОС=ОВ : ОD и ОР : ОВ=ОС : ОА,

из которых следует равенство ОМ : ОР=ОА : ОD. Далее по теореме, обратной теореме Фалеса следует утверждение задачи.

5. Ответ: все углы по 60.

Решение. Возможны два случая: 1) треугольник АВС равнобедренный с основанием АС (рис. а), 2) треугольник АВС равнобедренный с основанием АВ (рис. б).

Проведем медиану СС₁ и точку пересечения медиан обозначим буквой М. Тогда, по теореме о сумме углов для треугольника АВМ находим АМВ=120. Поскольку треугольник АВС равнобедренный, то среди углов АВМ, ВМС и СМА есть два равных. Величина одного из трех углов АВМ, ВМС, СМА равна 120. Тогда третий из этих углов также равен либо 120=360-2120, либо Получаем, что эти все три угла равны 120. Тогда ВМА₁=180120=60, а отрезок МА₁ в результате является и биссектрисой, и медианой треугольника ВМС, а, следовательно, и высотой. Значит, АА₁ – медиана и высота треугольника АВС. Аналогичное утверждение верно и для отрезков ВВ₁ и СС_1. Тогда треугольник АВС – равносторонний и все его углы равны 60.

В С1 М А С А1 В1

С В1 А1 М А В С1

Ответы, указания, решения

10 Класс

1. Ответ: в 9 раз.

Решение. Всего улитка путешествовала по бамбуку 16 часов. Пусть, поднимаясь вверх по бамбуку, улитка проползла расстояние равное х, а за 1 час отдыха и 8 часов спуска улитки бамбук подрос на у. Тогда, спускаясь вниз, улитка проползла х+у. Составим выражения для определения скорости улитки при движении вверх по бамбуку и при спуске . Получаем:

,

,

.

Так как бамбук подрос на у за 9 часов, скорость его роста равна . Выполняя деление последнего равенства на 7, получаем:

,

откуда

.

Значит, скорость роста бамбука в 9 раз меньше скорости улитки.

2. Ответ: 25%.

Решение. Пусть М – акционер, который владеет наибольшим процентом акций - х%. Разобьем остальных 99 акционеров на три группы А, В, С по 33 человека в каждой, и пусть каждая группа владеет а%, b% и с% акций соответственно. Тогда 100–х=а+b+с. Получаем:

2(100–х)=2(а+b+с)=(а+b)+(b+с)+(а+с).

Поскольку каждая из сумм (а+b), (b+с), (а+с) соответствует 66 акционерам, то согласно условию (а+b)+(b+с)+(а+с)50+50+50, то х25.

Приведем пример такого распределения акций. Если каждый из 99 акционеров, кроме Х, владеет % акций, то любые 66 из них владеют % акций, а любые 66, включая Х, владеют более 50%, при этом Х владеет ровно 25% акций.

3. Доказательство. Составим разность

a²+b²+c²–abc=

.

4. Ответ: .

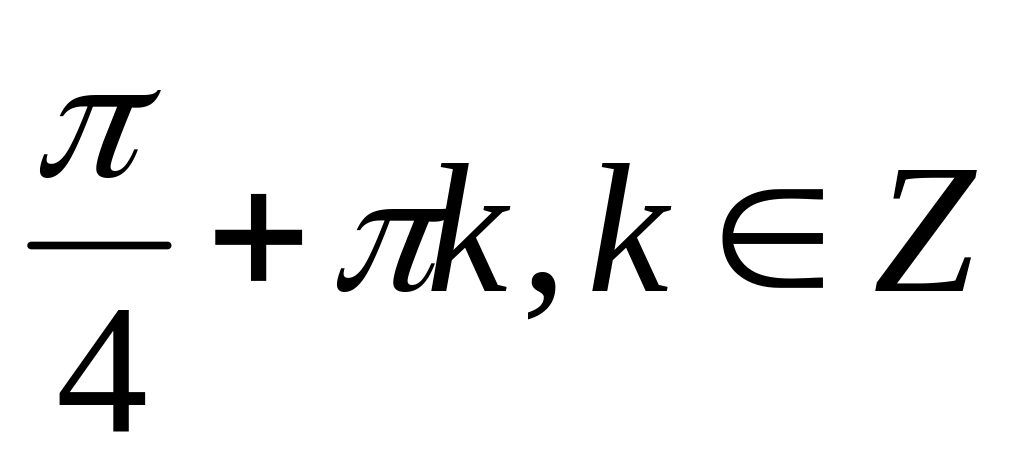Решение. Поскольку , то может принимать только три значения: 0, 1, 2.

Случай =0 невозможен, так как тогда =0, т.е. не определен.

В случае =1 имеем

, т.е. .

Однако, учитывая условие =1, получаем х= .

Случай =2 невозможен, так как тогда , т.е. =0.

5. Ответ:45°.

Решение. Поскольку диагональ АС является серединным перпендикуляром к диагонали ВЕ, то ВТ=ТЕ. Тогда из равенства МТ=ЕТ следует ВТ=МТ. Значит, треугольник ВТМ – равнобедренный. Так как РВТ=АВС–МВТ=90°–МВТ и ВРТ=90°–МВТ, то РВТ=ВРТ.
В М С Т А Е Р	Значит, треугольник РВТ – равнобедренный. Поскольку ВТ=МТ=РТ=ЕТ, то точки В, М, Р, Е лежат на окружности с центром в точке Т. А так как углы МРЕ и МВЕ опираются на одну и ту же дугу окружности, то они равны и МВЕ=МРЕ=45°.