Лекция 1

Объект (экспериментальная установка)

x_i – входы, факторы, i=1…k

y - выход, отклик

Математическая модель объекта

x_i – независимая переменная, i=1…k

y - зависимая переменная

p_j - параметры модели, j=1…m

Цель математической обработки эксперимента:

1. Найти вид математической модели

2. Определить параметры модели

3. Оценить точность приближения

4. Оценить погрешность в определении параметров

Способы обработки эксперимента:

1. Графический

Достоинство – наглядность

Ограничение – один фактор, два параметра

Модель линейная или линеаризованная.

Линеаризация

Оценка точности приближения и оценка точности параметров.

Влияние масштаба

2. Прямой поиск

Сравнение результатов эксперимента с результатами расчета по модели

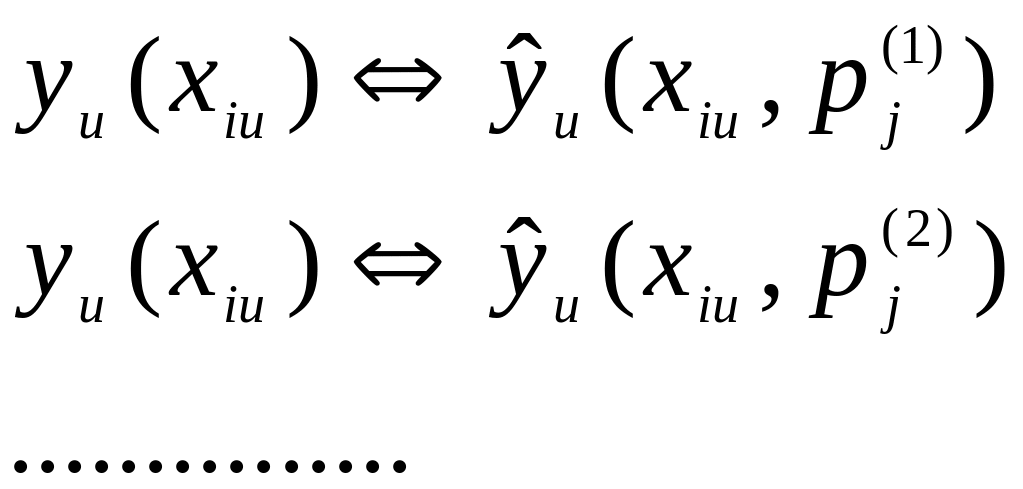
Пример для

						…	…
						…	…
						…	…
						…	…
…	…	…	…	…	…	…	…

Недостаток: большой объем расчетов, необходимость задать область поиска.

Преимущество: нет ограничения на число факторов и параметров.

Методика оценки точности приближения и точности оценки параметров не разработана.

Нет методики выбора модели

3. Статистический анализ результатов эксперимента.

Цель математической обработки эксперимента:

1. Найти вид математической модели

2. Определить параметры модели

3. Оценить точность приближения

4. Оценить погрешность в определении параметров

1. Найти вид математической модели

Пока ограничимся тем, что зададим модель в самом общем виде, позже вернемся к этому вопросу.

2. Определить параметры модели

Все это надо сделать, имея в своем распоряжении результаты эксперимента.

Таблица результатов эксперимента:

Номер опыта	Значения факторов (входов)				Результат (выход)
			.........
1			.........
2			.........
...	...	...	.........	...	...
u			.........
...	...	...	.........	...	...
n			.........

Эту таблицу можно представить в матричной форме, записав матрицу факторов

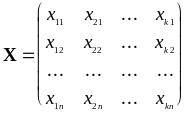
и матрицу (вектор) результатов (выходов):

Теперь надо определить параметры модели, которые наилучшим образом соответствуют эксперименту. Критерий соответствия – сумма квадратов отклонений экспериментальных и расчетных значений откликов (выходов) и .

, (2.2)

,

где:

(2.3)

Условием минимума этой функции по переменным будет равенство нулю ее частных производных по всем :

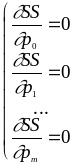
(2.4)

и затем:

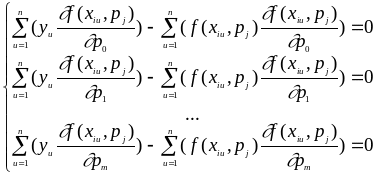(2.5)

Решив эту систему уравнений можно найти наилучшие параметры модели. Если бы система была линейна по параметрам, задача определения параметров была бы решена, так как она имела бы одно решение, один набор параметров. Система нелинейных уравнений может иметь несколько решений. Возвращаемся к недостаткам прямого поиска.

Естественным предложением в этой ситуации является представление функции нелинейной по параметрам в виде линейной функции, разложением функции в ряд :

(2.6)

,

где к - число реальных входных факторов.

Если кроме реальных входных факторов, ввести формальные факторы, составляемые как произведения реальных факторов и фактор , получим набор факторов:

С учетом этого уравнение модель преобразуется в

(2.7)

Теперь полином линеен не только по параметрам, но и по факторам, причем число факторов равно числу коэффициентов.

Пример:

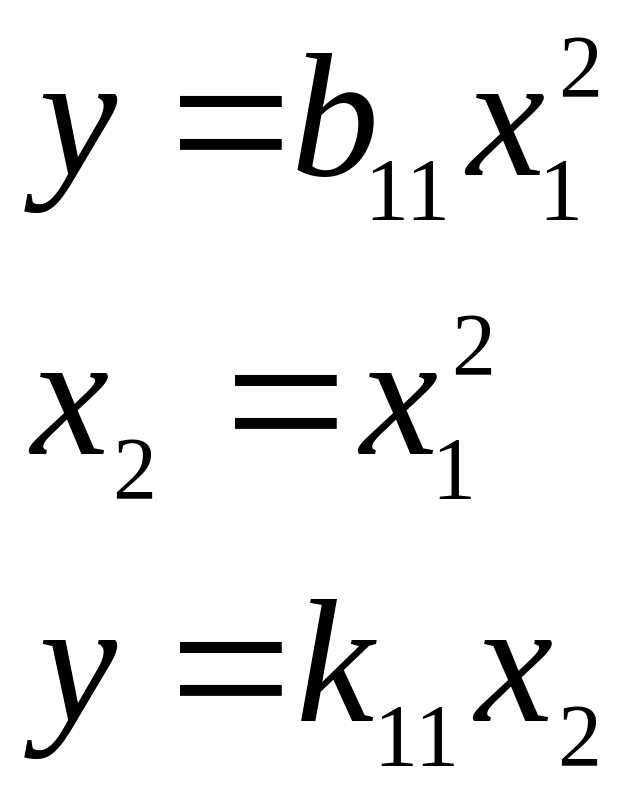
Преимущество такого преобразования – возможность однозначно решить систему нормальных уравнений.

Недостаток – потеря исходного физического смысла параметров модели, параметры модели заменяются коэффициентами полинома.

Изменяется число коэффициентов и число факторов, к реальным факторам добавляются фиктивные. С учетом этого таблица результатов опыта изменится.

Номер опыта	Значения факторов (входов)					Результат (выход)
				.........
1	1			........
2	1			.........
...	1	...	...	.........		...
u	1			.........
...	1	...	...	.........		...
n	1			.........

В матричной форме:

. .

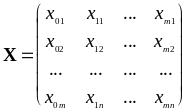
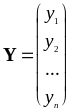
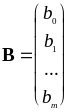
Система уравнений (2.5) очень сильно упростится за счет членов, содержащих частные производные:

Пример:

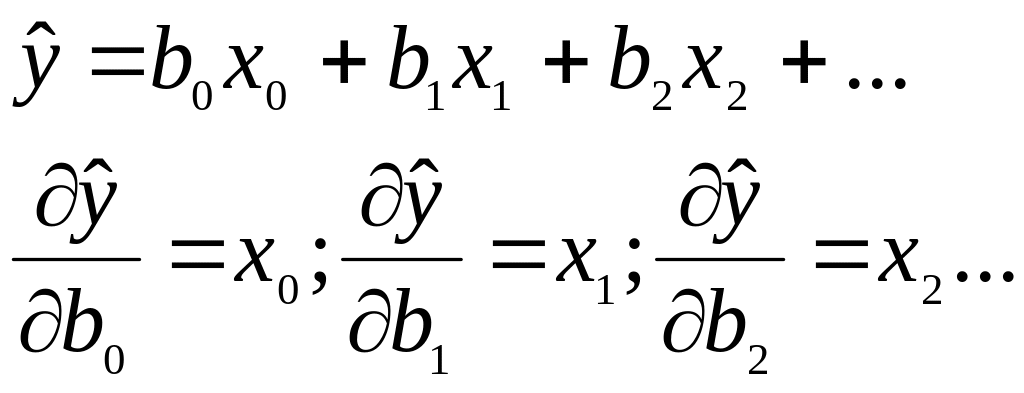
Проведя эти замены, перепишем систему (2.5)

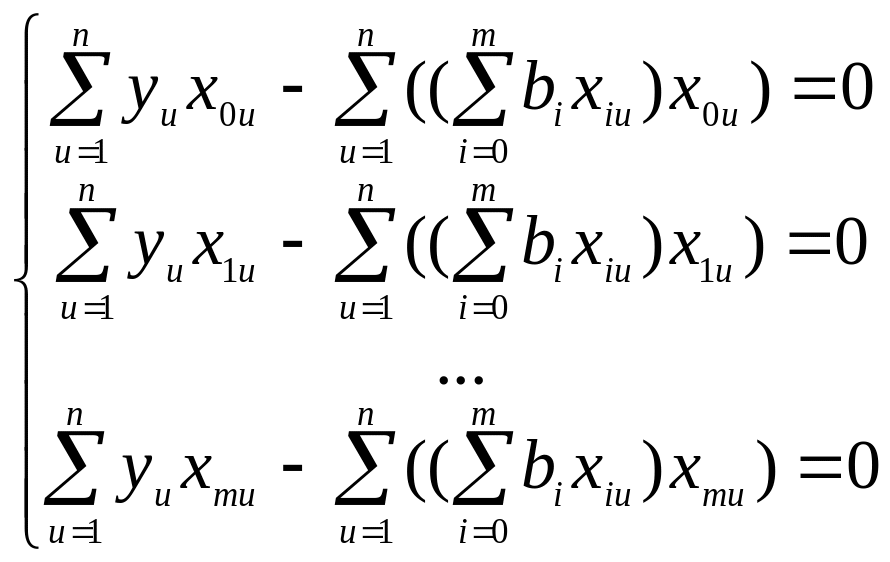(2.8)

Проведя простые преобразования системы (2.8), получим:

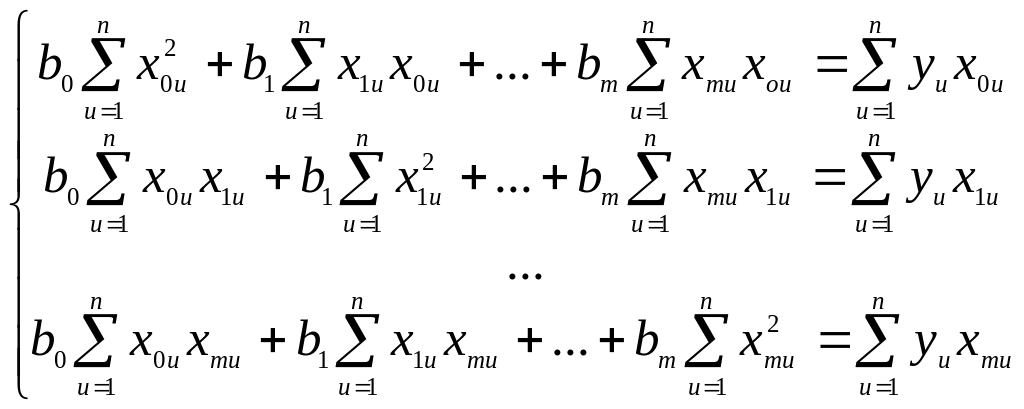(2.9)

Можно показать, что последняя система запишется в виде матричного уравнения:

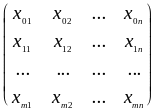. . (2.10)

или

Решая это матричное уравнение относительно вектора , получим

(2.11)

Матрица ( ) называется информационной матрицей, а матрица, полученная в результате обращения - ковариационной.

Для решения матричного уравнения (2.11) нужна матрица X и вектор Y. Вектор Y известен, а для написания матрицы X нужно знать число факторов, т.е конкретный вид полинома. Снова отложим решение этого вопроса на потом.

Точность обращения матрицы очень сильно связана с относительными значениями элементов матрицы и со структурой матрицы. Поскольку эта матрица содержит в качестве элементов значения экспериментальных факторов, т.е. связана с условиями эксперимента (значениями входов), то повлиять на ее структуру можно, поставив эксперимент определенным образом. Мы приходим к идее планирования эксперимента при нахождении параметров модели.