1.2.2. Построение эпюры напряжений.
Нормальное напряжение σ(z) распределяются равномерно по сечению
Где N(z) – продольная сила, А(z) – площадь поперечного сечения.
4
Для
определения опасного сечения стержня,
в котором возникает максималь-ное
напряжение, определим напряжение в
долях 1/A0. На
участке АВ ( 0
≤ z1
≤ l1
= 0,2 м )
нормальные напряжения
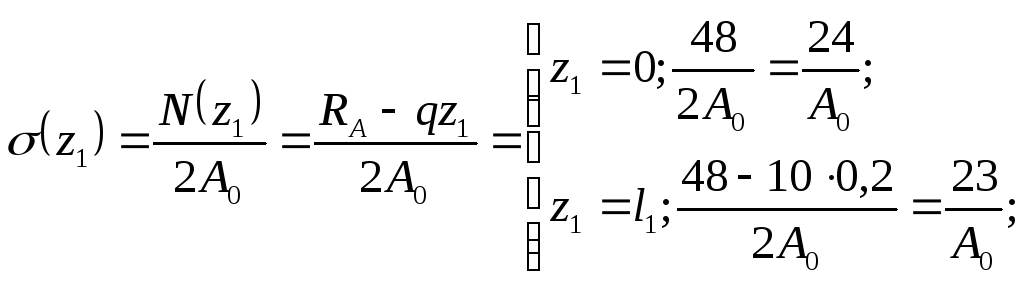
Участок ВС ( 0 ≤ z2 ≤ l2 = 0,6 м ).
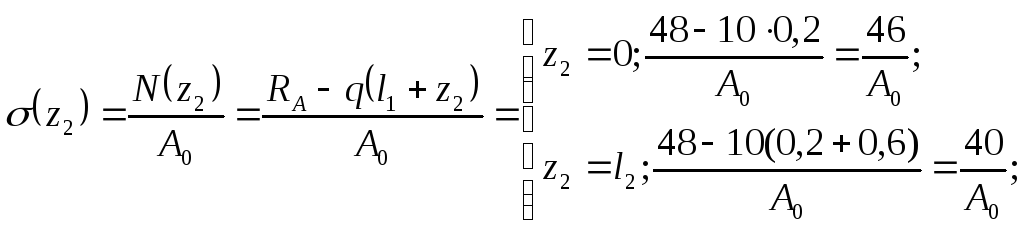Участок
CD( 0
≤ z3
≤ l3
= 0,5 м ).
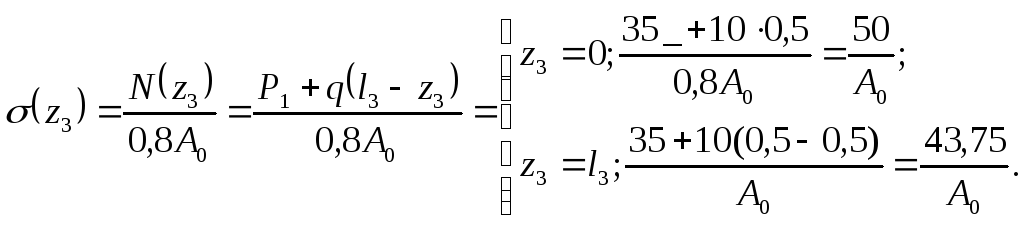
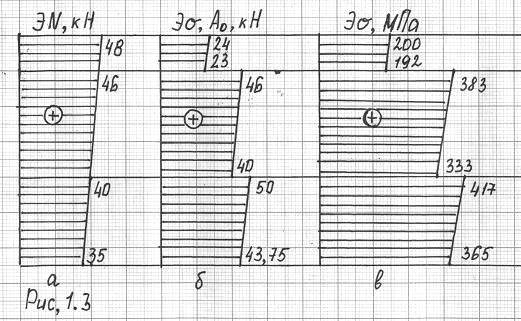
По полученным данным построим Эσ А0 (рис 1.3, б)
1.2.3. Расчет на прочность. Подбор сечения.
По эпюре напряжений
видно, что опасным является сечение С,
[σmax]=
.
Условие прочности при растяжении – сжатии имеет вид
где [σ] – допустимое напряжение, которое определено выше для материала Д16 и равно [σ] = 418МПа.
Тогда условие прочности примет вид
,откуда А0:
А0
.
При этом А1=2А0=2∙120=240мм2; А2=А0=120мм2; А3=0,8А0=0,8∙120=96мм2.
Определим напряжения, действующие в сечениях при выбранном значении А0.
Участок АВ:
5
Участок ВС:
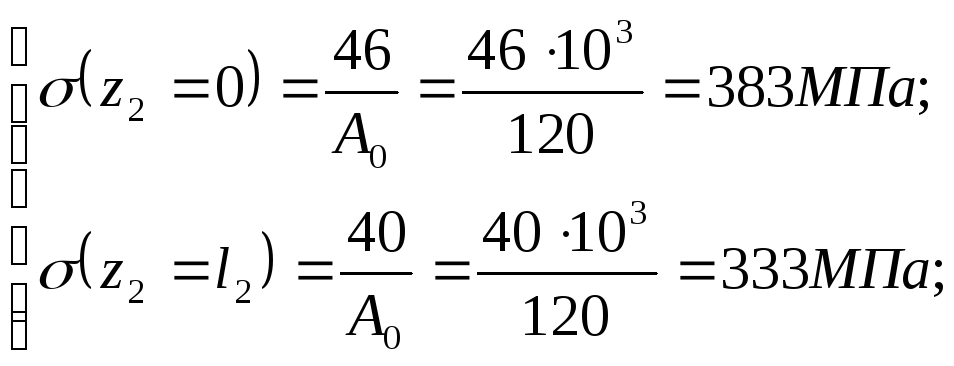
Участок CD:
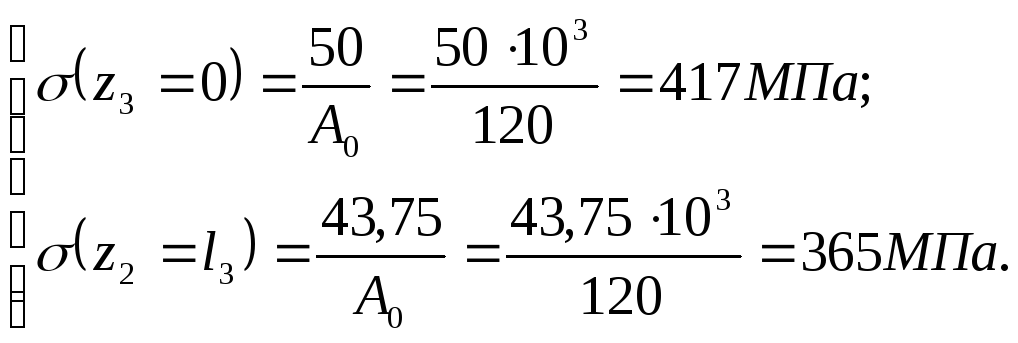
По полученным данным строим эпюру действующих в стержне нормальных напряжений (рис 1.3, в).
6
1.3. Расчет на жесткость стержня постоянного сечения.
Для стержня из дюралюминия Д16, площадью сечения 10 см2, представленного на рисунке 1.4, необходимо построить эпюры продольных сил и осевых перемещений, выполнить расчет на жесткость.
1.3.1. Построение эпюр продольных сил и перемещений.
Построение эпюр продольных сил.
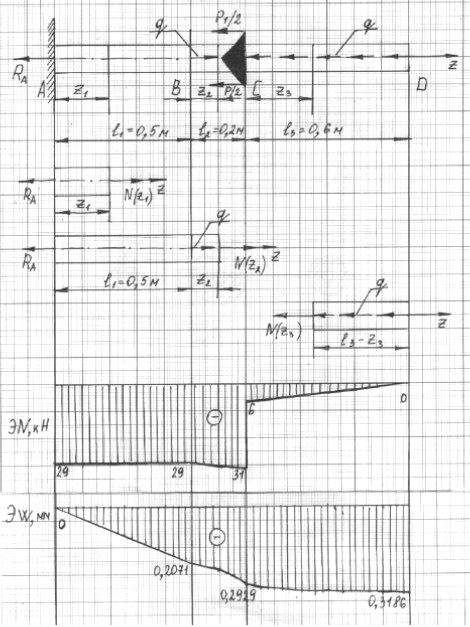
Построение эпюр продольных сил направим вдоль оси стержня ось z (рис 1.4). Составим уравнение равновесия системы:
6
Рис. 1.4
7
Разобьем стержень на 3 участка АВ, ВС и СD, проведем на каждом из них произвольные сечения с заданными координатами z1, z2, z3.
На участке АВ ( 0 ≤ z1 ≤ l1 = 0,5 м ). Отбросив правую часть, её действие заменим продольной силой N(z1).
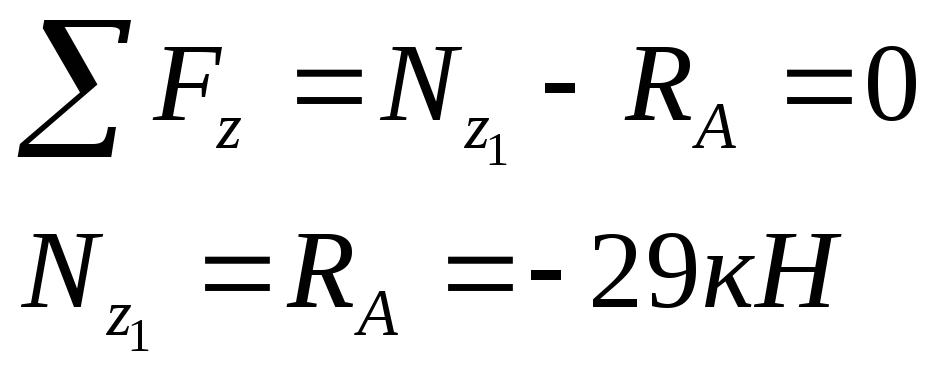
Участок ВС ( 0 ≤ z2 ≤ l2 = 0,2 м )
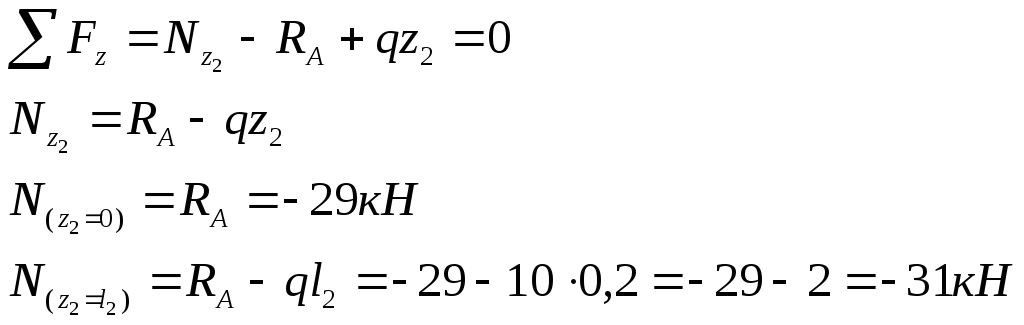
Участок СD ( 0 ≤ z3 ≤ l3 = 0,6 м )
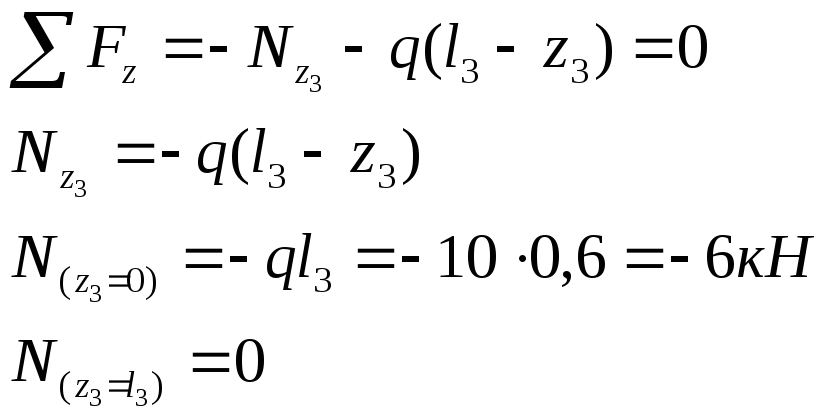
По полученным данным строим эпюру ЭN (рис 1.4).
Построение эпюры перемещений.
Запишем уравнение для перемещения w(z) сечений, считая площади сечений известными.
w(z) = w0 + ∆l(z),
где w0 – перемещение в начале участка, определяемое начальными условиями;
∆l(z) – удлинение участка (абсолютная деформация участка стержня).
Если продольная сила N(z) зависит от координат сечения z,
Для дюралюминия Д16 Е = 0,7 · 105 МПа. В расчетах примем жесткость сечения при растяжении-сжатии ЕА = 0,7 · 105 · 10 · 102 = 7 ∙ 104 кН.
Рассмотрим участок АВ ( 0 ≤ z1 ≤ l1 = 0,5 м ). Перемещения произвольного сечения z1.
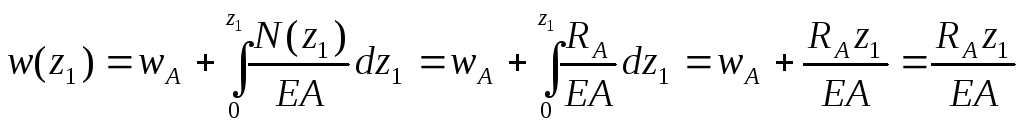
8
Функция w(z1)
– линейная. Так как в сечении А заделка,
то при z1=0
w(z1=0)
= 0; при z1
= l1
= 0,5
м wB
(z1
= 0,5 м ) = 
Участок ВС ( 0 ≤ z2 ≤ l2 = 0,2 м ). Перемещение произвольного сечения z2.
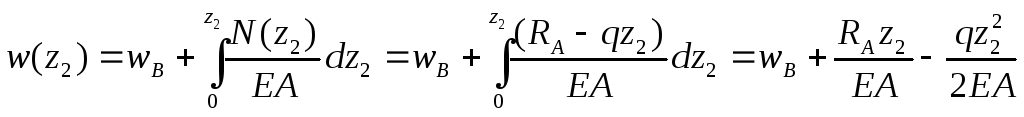
Функция w(z2) – квадратичная парабола.
При z2=0 w(z2=0) = wB(z2=0) = – 0,2071 мм;
при z2=l2/2=0,1м
w(z2=l2/2=0,1м)=
=
при z2
=l2=
0,2 м wC(z2
=l2=0,2
м) = =
Участок СD ( 0 ≤ z3 ≤ l3 = 0,6 м ). Перемещение произвольного сечения z3
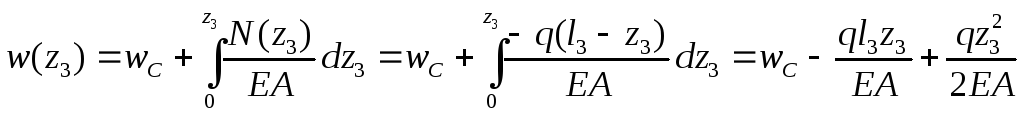
Функция w(z3) – квадратичная парабола.
При z3=0 w(z3=0) = wС(z3=0) =– 0,2929 мм;
при z3=l3/2=0,3м
w(z3=l3/2)=
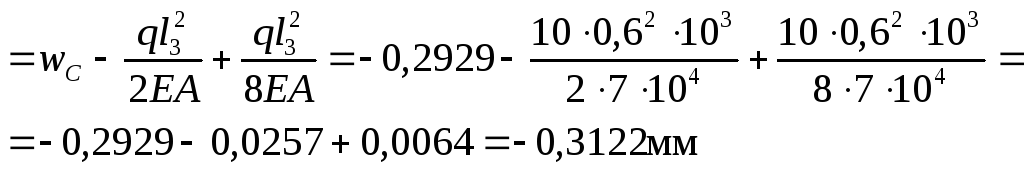
при z3 = l3= 0,6м w(z3 = l3= 0,6м)=
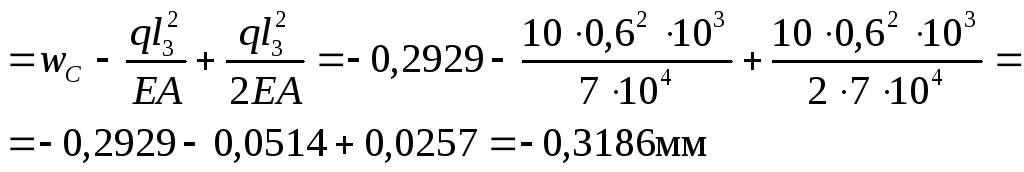
По полученным данным строим эпюру перемещений ЭW (рис. 1.5).
1.3.2. Расчет на жесткость.
Условия жесткости при растяжении – сжатии
∆l ≤ [ l ],
где ∆l – удлинение стержня, [ l ] – допустимое удлинение. В данном случае удлинение жесткости должно выполняться для участков ВС и ВD
∆lBC ≤ [ l ]BC, ∆lВD ≤ [ l ]ВD
Величина ∆l=0,001L принимается в долях от суммарной длины L.
[ l ]BC = 0,001·l2 = 0,001·0,2 = 0,2·10-3м = 0,2 мм
[ l ]СD = 0,001· l3 = 0,001·0,6 = 0,6·10-3м = 0,6 мм
Запишем условие жесткости
[ ∆l ]BC = 0,0858 мм < [ l ]BC = 0,2 мм
[ ∆l ]СD = 0,0256 мм < [ l ]СD = 0,6 мм.
Условие жесткости выполняется.
9
