15

КОСМИЧЕСКИЕ И НАЗЕМНЫЕ СИСТЕМЫ РАДИОСВЯЗИ И СЕТИ

ТЕЛЕРАДИОВЕЩАНИ

Лекция 2: Телефонный трафик в сетях связи

с подвижными объектами

План занятия:

Время	№ п/п	Содержание раскрываемого вопроса:
10 мин.	1.	Общая постановка задачи
35 мин.	2.	Система массового обслуживания с отказами. Уравнения Эрланга
35 мин.	3.	Трафик и определение размеров соты

1. Общая постановка задачи

Цель развертывания сотовой сети состоит в обеспечении требуемого трафика. Под трафиком в данном случае будем понимать абонентскую нагрузку, которую должна предоставить сотовая сеть. Эта нагрузка может быть двух типов, в зависимости от принципа организации каналов связи. При использовании коммутируемых каналов канал связи предоставляют абоненту на все время сеанса связи. Этот способ использования каналов характерен для обычной телефонии, но его применяют и при передаче данных по коммутируемым каналам. При этом канал занят независимо от того, следует ли активный этап передачи информации или пауза. Другой подход типичен для пакетной передачи данных. В том случае трафик определяют объемом переданной информации Q бит, который характеризуют скоростью передачи информации J (бит/с) и временем передачи пакетов t_пак (с). Так определяют трафик при использовании технологии GPRS (General Packet Radio Service). В рамках данного курса ограничимся рассмотрением трафика по коммутируемым каналам.

Так как трафик по коммутируемому каналу определен временем занятия канала, то его характеризует временная величина, выражаемая в эрлангах (А.К. Эрланг - датский специалист в области телефонии, работавший в 20-х годах прошлого века).

1 Эрл - это трафик, при котором канал(ы) связи занят(ы) один час в течение часа времени (рис. 1). На рис. 1 показано несколько вариантов трафика, когда занят как один, так и несколько каналов.

П ри планировании сети используют взаимосвязь между тремя величинами:

• число коммутируемых каналов N_с;

• трафик в эрлангах ;

• вероятность отказа в предоставлении канала в час наибольшей нагрузки

(ЧНН) Р_отк.

Последняя величина характеризует качество обслуживания (GoS - Grade of Service) абонентов в сетях с коммутируемыми каналами. Три вышеназванные величины связаны между собой статистически при следующих принятых допущениях:

• число активных абонентов в любой момент времени гораздо меньше общего числа абонентов,

• относительное время занятости абонентом канала связи мало,

• трафик распределен по закону Пуассона,

• все абоненты имеют одинаковый приоритет,

• в системе отсутствуют очереди (ожидание) при занятости всех каналов; в этом случае вызов снимают.

2. Система массового обслуживания с отказами.

Уравнения Эрланга

Системы массового обслуживания делятся на два основных типа:

а) системы с отказами, б) системы с ожиданием.

В системах с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, немедленно получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует.

В системах с ожиданием заявка, заставшая все каналы занятыми, не покидает систему, а становится в очередь и ожидает, пока не освободится какой-нибудь канал.

Действующие системы связи с подвижными объектами в силу, прежде всего, ограниченности энергетических ресурса мобильных станций относятся к системам с отказами. Рассмотрим систему с отказами/

Пусть имеется n-канальная система массового обслуживания с отказами. Рассмотрим ее как физическую систему X с конечным множеством состояний:

х₀ – свободны все каналы,

х₁ – занят ровно один канал,

х_к – занято ровно k каналов,

х_п – заняты все п каналов.

Схема возможных переходов дана на рис. 2.

О пределим вероятности состояний системы:

(k=0, 1, …п) для любого момента времени t.

Введем следующие допущения:

1. поток заявок – простейший, с плотностью ;

2. время обслуживания Т_об – показательное, с параметром

(t>0). (1)

Заметим, что параметр . в формуле (1) аналогичен параметру показательного закона распределения промежутка Т между соседними событиями простейшего потока:

(t>0). (2)

Параметр имеет смысл «плотности потока заявок». Аналогично, величину , можно истолковать как «плотность потока освобождений» занятого канала. Действительно, представим себе канал, непрерывно занятый (бесперебойно снабжаемый заявками); тогда, очевидно, в этом канале будет идти простейший поток освобождений с плотностью (л.

Так как оба потока – заявок и освобождений – простейшие, то процесс, протекающий в системе, будет марковским.

Рассмотрим возможные состояния системы и их вероятности

, , ... . (3)

Очевидно, для любого момента времени будет выполняться нормировочное условие

(4)

Составим дифференциальные уравнения для всех вероятностей (3), начиная с . Зафиксируем момент времени t и найдем вероятность того, что в момент система будет находиться в состоянии х₀ (все каналы свободны). Это может произойти двумя способами (рис 3):

А – в момент t система находилась в состоянии х₀, а за время не перешла из нее в состояние х₁ (не пришло ни одной заявки);

В – в момент t система находилась в состоя­нии х₁, а за время канал освободился, и система перешла в стояние х₀).

Возможностью «перескока» системы через состояние (например, из х₂ в х₀ через х₁) за малый промежуток времени можно пренебречь, как величиной высшего порядка малости по сравнению с Р (А) и Р (В).

По теореме сложения вероятностей имеем

. (5)

Найдем вероятность события А по теореме умножения. Вероят­ность того, что в момент t система была в состоянии х₀, равна . Вероятность того, что за время не придет ни одной заявки, равна . С точностью до величин высшего порядка малости

. (6)

Следовательно,

.

Найдем Р(В). Вероятность того, что в момент t система была в состоянии x₁ равна . Вероятность того, что за время канал освободится, равна ; с точностью до малых величин выс­шего порядка

.

Следовательно,

.

Отсюда

.

Перенося в левую часть, деля на и переходя к пределу при , получим дифференциальное уравнение для :

. (7)

Аналогичные дифференциальные уравнения могут быть составлены и для других вероятностей состояний.

Возьмем любое k (0<k<n) и найдем вероятность того, что в момент система будет в состоянии х_к (рис. 4).

Эта вероятность вычисляется как вероятность суммы уже не двух, а трех событий (по числу стрелок, направленных в состояние x_k):

А – в момент t система была в состоянии х_к (занято k каналов), а за время не перешла из него ни в х_к+1, ни в х_к-₁ (ни одна заявка не поступила, ни один канал не освободился);

В – в момент времени t система была в состоянии x_k-₁ (занято k-1 каналов), а за время перешла в состояние х_к (пришла одна заявка);

С – в момент времени t система была в состоянии x_k+1 (занято k+1 каналов), а за время один из каналов освободился.

Найдем Р(А). Вычислим сначала вероятность того, что за время не придет ни одна заявка и не освободится ни один из каналов:

.

Пренебрегая малыми величинами высших порядков, имеем

,

откуда

.

Аналогично

,

и

.

Отсюда получаем дифференциальное уравнение для p_k (t) (0 < k < п):

.

С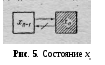оставим уравнение для последней вероятности (рис. 5). Имеем

.

где – вероятность того, что за время не освободится ни один канал; – вероятность того, что за время придет одна заявка.

Получаем дифференциаль­ное уравнение для :

.

Таким образом, получена система дифференциальных уравнений для вероятностей , , ... :

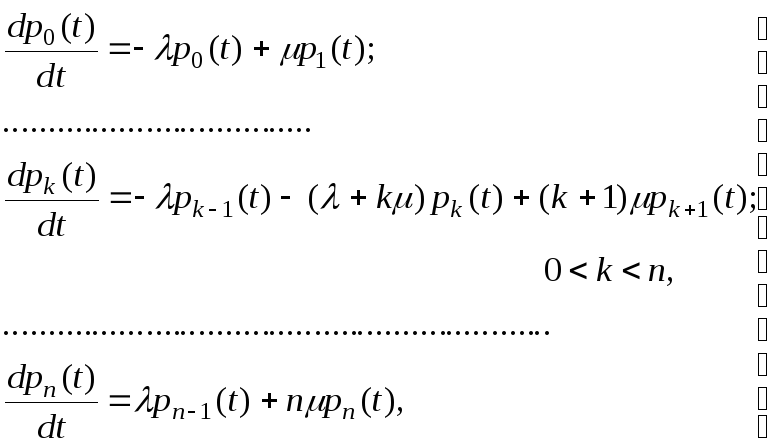(8)

Уравнения (8) называются уравнениями Эрланга. Интегрирование системы уравнений (8) при начальных условиях

, , ...

(в начальный момент все каналы свободны) дает зависимость для любого k. Вероятности характеризуют среднюю загрузку системы и ее изменение с течением времени. В частности, – есть вероятность того, что заявка, пришедшая в момент t, застанет все каналы занятыми (получит отказ):

.

Величина называется относительной пропускной способностью системы. Для данного момента t это есть отношение среднего числа обслуженных за единицу времени заявок к среднему числу поданных.

Система линейных дифференциальных уравнений (8) сравнительно легко может быть проинтегрирована при любом конкретном числе каналов п. Заметим, что при выводе уравнений (.8) мы нигде не пользо­вались допущением о том, что величины и (плотности потока заявок и «потока освобождений») постоянны. Поэтому уравнения (8) остаются справедливыми и для зависящих от времени и , лишь бы потоки событий, переводящих систему из состояния в состояние, оставались пуассоновскими (без этого процесс не будет марковским).