Код Хаффмана.

Код Хаффмана близок к коду Ш-Ф, но является более экономичным. Относится к неравномерным обратимым кодам.

Тезис. Ни для какого другого метода кодирования букв некоторого алфавита среднее число элементарных сигналов, приходящихся на одну букву, не может быть меньше того, какой получается получается при кодировании по методу Хаффмана.

Алгоритм. Буквы алфавита A выписываются в основной столбец по убыванию вероятностей. Две последние буквы объединяются в одну вспомогательную букву и получяется новый алфавит A₁ из алфавита A путем однократного сжатия последней буквы. Затем вероятности букв, не участвующих в объединении и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей. Процесс сжатия алфавита A_i повторяется до тех пор, пока не получится единственная вероятность буквы = 1, при этом условимся приписывать буквам a_i 0 и 1.

Пример. A = {0,05; 0,2; 0,4; 0,2; 0,05; 0,1}.

A3	0,4	0	0,4	0	0,4	0	0,4	0	0,6	1
A2	0,2	10	0,2	10	0,2	10	0,4	11	0,4	0
A4	0,2	111	0,2	111	0,2	111	0,2	10
A6	0,1	1101	0,1	1101	0,2	110
A1	0,05	11001	0,1	1100
A5	0,05	11000

A₁ → 11001

A₂ → 10

A₃ → 0

A₄ → 111

A₅ → 11000

A₆ → 1101

Кодирование некоторого алфавита по методам Ш-Ф и Х не является однозначно определенной процедурой. Например, можно при кодировании поменять местами 0 и 1. Можно построить более существенно отличный код Х, когда вновь полученная вероятность ставится в ряд на первое место с такими же по величине вероятностями.

Основная теорема кодирования. При кодировании сообщения разбитого на N буквенные блоки можно, выбрав N достаточно большим, добиться того, чтобы среднее число bin элементарных сигналов, приходящихся на одну букву исходного сообщения, было наиболее близко к энтропии.

8. Частотная модуляция. Частотный детектор. Частотные модуляторы

G - генератор

УДЧ – управляемый делитель частоты

ФНЧ – фильтр низких частот

> - усилитель

Форм. – формирователь

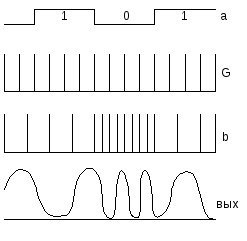
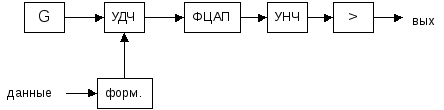
ФЦАП – функциональный цифро-аналоговый преобразователь

УНЧ – усилитель низких частот

Схема ФЦАП

9. Фазовая модуляция. Виды фм. Реализация двукратного фм. Фазовые модуляторы

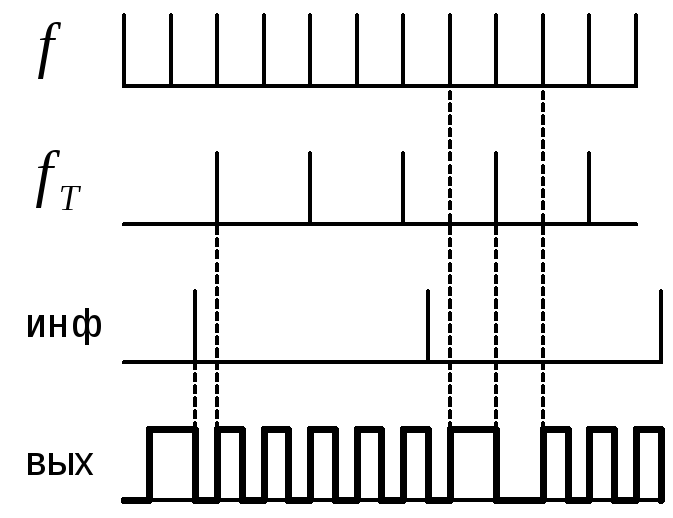
00 – 0

10 – 90

11 - 180

01 - 270

Предыдущие 2 такта	Последующие 2 такта	3 значения фазы
a1a2	b1b2	пред.	относ. пред	Относ. ‘0’
00	00	0	0	0
00	01	0	90	90
00	10	0	180	180
00	11	0	270	270
01	00	90	0	90
01	01	90	90	180
01	10	90	180	270
01	11	90	270	0

- уже минимизировано

Эти выражения можно минимизировать 