28. Нахождение кратчайших путей в сети (методом Рагинского)

Рассмотрим конкретный пример. Зададим сеть.

Матрица связности сети:

	1	2	3	4	5	6	7	8	9
1	–	10					3	6	12
2	10	–	18				2		13
3		18	–	25		20			7
4			25	–	5	16	4
5				5	–	10		23
6			20	16	10	–	14	15	9
7	3	2		4		14	–		24
8	6				23	15		–	5
9	12	13	7			9	24	5	–

Найдем стоимость каждого из соединений (первое число – стоимость ранее найденного пути).

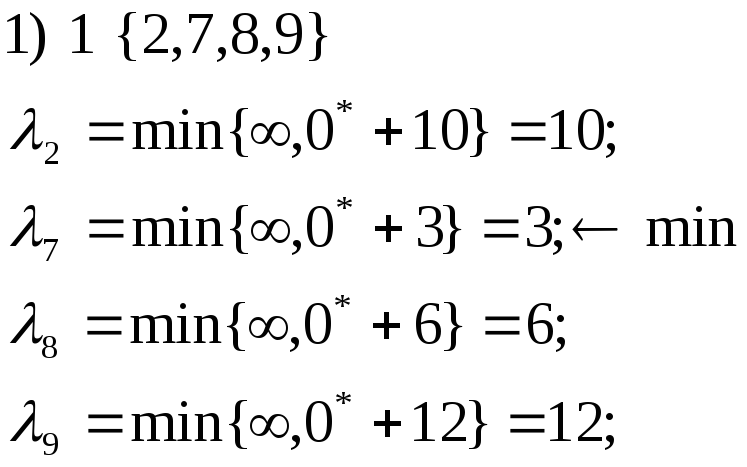
Найдем стоимость соединений от 1 узла к 2, 4, 6, 9 через 7.

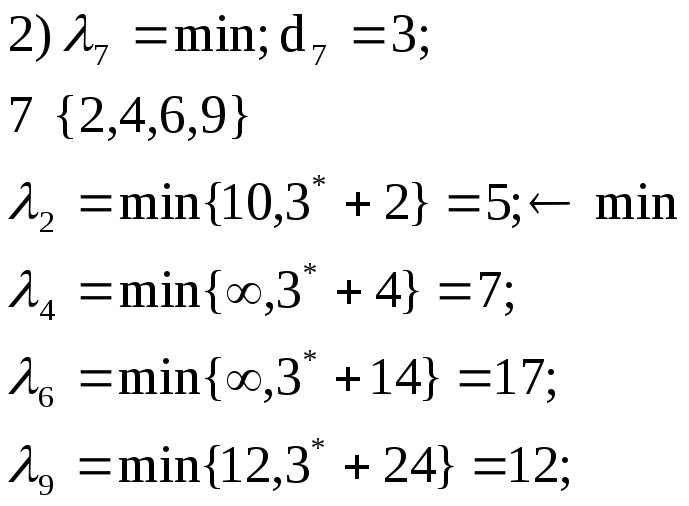
3) Прописываем точку 2.

Далее определяем маршруты для всех оставшихся точек.

Получены маршруты. Составим таблицу маршрутизации для всех оставшихся точек сети.

1→7

1→2→7

1→9

29. Принципы маршрутизации по методу Форда-Беллмана.

В современных сетях обычно используются динамические методы маршрутизации. Алгоритм Форда-Беллмана относится к так называемому методу дистанционно-векторной маршрутизации. Все алгоритмы дистанционно-векторной маршрутизации, в том числе и алгоритм Форда-Беллмана, действуют следующим образом. Каждый маршрутизатор содержит таблицу (вектор), в которой перечисляются кратчайшие пути к каждому получателю. Для обновления данных эих таблиц производится обмен данными с соседними маршрутизаторами.

Таблицы с которыми работают маршрутизаторы содержат записи о каждом маршрутизаторе подсети. Каждая запись состоит из двух частей: номера оптимальной линии для данного получателя и оценки расстояния(времени) прохождения пакета до этого получателя.

Предполагается, что маршрутизаторам известно расстояние до каждого из соседей. Если в качестве единицы измерения используется время задержки, то маршрутизатор в состоянии измерить это время с помощью специального эхо-пакета (ECHO).

Для примера предположим, что в качестве единицы измерения используется время, и оно известно каждому маршрутизатору для каждого из своих соседей. Через равные интервалы времени каждый маршрутизатор посылает своим соседям список с оценками задержек для получателя. Он также получает похожие списки от всех своих соседей. Пусть одна из таблиц пришла от соседа Х, и в ней указано, что время распространения от маршрутизатора Х до j равно Х_j. Если маршрутизатор знает, что при посылке пакета Х, время задержки равно m, то тогда задержка при посылке пакета до j составит X_j+m. Выполнив такие расчеты для всех пришедши таблиц, маршрутизатор может вычислить наилучшие значения, и в дальнейшем поместить их в свою таблицу. Стоит отметить, что старая таблица в вычислении новой не используется.

Проблема счета до бесконечности. Алгоритм дистанционно векторной маршрутизации хорош в теории, однако может сходится к верному ответу очень долго. Рассмотрим случай 4-х маршрутизаторов расположенных в линию. Пусть сначала все маршрутизаторы работали, и расстояние между каждой парой равно 1, для простоты. Пусть теперь маршрутизатор А(или линия соединения А с В) вышел из строя. В пытается послать ему пакет, но он не доходит. Тогда при обмене таблицами В увидит, что есть путь к А через С по длине равный 2, а тогда путь к А от В через С равен 3. Такая ситуация будет продолжаться неограниченно долго, причем для всех марщрутизаторов вышеприведенной сети. В этом случае стоит ограничить максимальное время пересылки пакета на каждом маршрутизаторе, но это стоит делать очень аккуратно, т.к. это может привести к тому, что медленный канал связи может быть сочтен неработающим.