Принципы маршрутизации по методу Дейкстры.
Алгоритм Дейкстры предназначен для определения кратчайшего пути во взвешенном графе по между заданными исходной и конечной вершинами. Этот алгоритм, в отличие от некоторых других работает для любых графов – ориентированных и неориентированных, имеющих циклы. Вычислительная сложность алгоритма Дейкстры - N∙logN, что является минимальной вычислительной сложностью для алгоритмов отыскания кратчайшего пути.
Пусть топология сети задана некоторым взыешенным графом, причем вершины являются маршрутизаторами, а ребра – связями между ними. Для того, чтобы найти кратчайший путь между заданными маршрутизаторами A и B, по алгоритму Дейкстры, необходимо выполнить следующие шаги:
Упростить граф, путем удаления кратных ребер(дуг) и петлей. При удалении кратных ребер(дуг), они заменяюся одним ребром(дугой), имеющим вес, равный минимальному из весов удаленных ребер.
Приписать всем вершинам, кроме А временные пометки “”, а вершине А приписать постоянную пометку “0”, и сделать вершину А текущей.
Для всех вершин, связанных с текущей, найти ребро с минимальным весом, ведущее из текущей вершины в рассматриваемую. Сравнить пометку рассматриваемой вершины, с суммой пометки текущей вершины и веса минимального ребра. Пометке рассматриваемой вершины присвоить наименьшее из этих двух значений.
Рассмотреть все вершины с временными пометками, и найти вершину с минимальной временной пометкой. Объявить эту пометку постоянной, данную вершину сделать текущей. Если это не вершина B, перейти на шаг 2, иначе на 4.
Пометка вершины B является длиной минимального пути из вершины A в вершину B.
Для того, чтобы отыскать маршрут с минимальной длиной из вершины А в вершину В, после работы алгоритма Дейкстры производят следующий действия:
Из графа удаляются все вершины с временными пометками, удаляются все инцидентные им ребра.Вершина В делается текущей.
Рассматриваются все вершины, из которых можно попасть в текущую. Из них выбирается та, сумма пометки которой и веса ребра ведущего в текущую вершину равна пометке текущей вершины. Выбранная вершина входит в минимальный путь, и делается текущей. Если это не вершина А, то шаг 7 выполняется еще раз, иначе алгоритм заканчивает свою работу.
Стоит учесть, что данный принцип маршрутизации предполагает наличие на каждом маршрутизаторе графа сети. Однако это практически невозможно в больших сетях, т.к. очень часто маршрутизаторы выходят из строя, подключаются новые, и т.д. именно поэтому данный метод называется статическим. Маршрутизация с помощью такого метода очень надежна и эффетивна, но только в случае надежности самих маршруизаторов. Поэтому данный метод в настоящее время имеет очень малое распространение, и не является основой ни одного применяемого протокола маршруизации.
Структурный анализ сетей. Определение путей по матричному методу любого ранга.
Рассмотрим пример структурного анализа сети
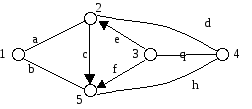
Пусть стоимости путей заданы матрицей
|
B1 = |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
a |
0 |
0 |
b | |
|
2 |
ā |
1 |
0 |
d |
c | |
|
3 |
0 |
ē |
1 |
q |
f | |
|
4 |
0 |
¯d |
¯q |
1 |
h | |
|
5 |
¯b |
0 |
¯f |
¯h |
1 |
Рассмотрим пути только 1-го ранга
γij = αi1β1j v αi2β2j v ... v αinβnj, где α – строка, β – столбец
|
γ15 = |
1 a 0 0 b |
|
b c f h 1 | |
|
b V ac V 0 V 0 V b = b Vac |
|
γ14 = |
1 a 0 0 b |
|
0 d q 1 ¯h | |
|
0 V ad V 0 V 0 V b¯h = ad V b¯h |
Возведем в квадрат
|
B12 = |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
a |
b¯f |
ad V b¯h |
b V ac | |
|
2 |
¯a V ¯bc |
1 |
c¯f V d¯q |
d V c¯h |
c V ¯ab V ¯d | |
|
3 |
|
|
1 |
|
| |
|
4 |
... |
|
|
1 |
| |
|
5 |
|
|
|
|
1 |