12. Марковский процесс и его свойства. Системы уравнений. Решение уравнений в стационарном режиме по заданному графу.

Моделирование по схеме марковских случайных процессов.

Пусть имеется некоторая физическая система S, состояние которой меняется с течением времени (под системой S может пониматься что угодно: техническое устройство, ремонтная мастерская, вычислительная машина и т.д.). Если состояние S меняется по времени случайным образом, говорят, что в системе S протекает случайный процесс.

Случайный процесс называется марковским процессом (или «процессом без последствия»), если для каждого момента времени t₀ вероятность любого состояния системы в будущем (при t  t₀) зависит только от её состояния в настоящем (при t = t₀) и не зависит от того, когда и каким образом система пришла в это состояние (т.е. как развивался процесс в прошлом).

Классификация марковских процессов.

Марковские случайные процессы делятся на классы. Случайный процесс (СП) называется процессом с дискретными состояниями, если возможные состояния системы

S₁, S₂, S₃, ...

можно перечислить. А сам процесс состоит в том, что время от времени система S скачком (мгновенно) перескакивает из одного состояния в другое.

С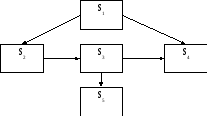уществуют процессы с непрерывными состояниеми. Будем рассматривать только СП с дискретными состояниями. Удобно пользоваться графом состояний: возможные состояния системы и возможные переходы.

СП называется процессом с дискретным временем, если переходы системы из состояния в состояние возможны только в строго определенные, заранее фиксированные моменты времени: t₁, t₂, ... . Если переход системы из состояния в состояние возможен в любой, наперед неизвестный случайный момент, то говорят о СП с непрерывным временем.

Марковские цепи с непрерывным временем. Уравнения Колмогорова.

На практике значительно чаще встречаются ситуации, когда переходы системы из состояния в состояние происходит в случайные моменты времени, которые заранее указать невозможно. Для описания таких процессов в ряде случаев может быть с успехом применена схема марковского случайного процесса с дискретными состояниями и непрерывным временем – непрерывная цепь Маркова. Покажем, как выражаются вероятности состояний для такого процесса. Пусть S = {S₁, S₂, ..., S_n}. Обозначим через p_i(t) – вероятность того, что в момент t система S будет находиться в состоянии . Очевидно. Поставим задачу – определить для любогоt p_i(t). Вместо переходных вероятностей P_ij введем в рассмотрение плотности вероятностей перехода

.

Еслине зависит отt, говорят об однородной цепи, иначе – о неоднородной. Пусть нам известны для всех пар состояний (задан размеченный граф состояний). Оказывается, зная размеченный граф состояний можно определить p₁(t), p₂(t), ..., p_n(t) как функции времени. Эти вероятности удовлетворяют определенного вида дифференциальным уравнениям, (уравнения Колмогорова).

Интегрирование этих уравнений при известном начальном состоянии системы даст искомые вероятности состояний как функции времени. Заметим, что p₁+p₂+p₃+p₄=1 и можно обойтись тремя уравнениями.

Правила составления уравнений Колмогорова. В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, соответствующий член имеет знак минус, если в состояние - знак плюс. Каждый член равен произведению плотности вероятности перехода, соответствующего данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.

Поток событий. Простейший поток и его свойства.

При рассмотрении процессов, протекающих в системе с дискретными состояниями и непрерывным временем, часто бывает удобно представить себе процесс так, как будто переходы системы из состояния в состояние происходят под действием каких-то потоков событий. Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то, вообще говоря, случайные моменты времени. Будем изображать поток событий последовательностью точек на оси времени ot. Положение каждой точки на оси случайно. Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени (редко встречается на практике). Рассмотрим специального типа потоки, для этого введем ряд определений.

1. Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени длиной τ зависит только от длины участка и не зависит от того, где именно на оси ot расположен этот участок (однородность по времени) – вероятностные характеристики такого потока не должны меняться от времени. В частности, так называемая интенсивность (или плотность) потока событий (среднее число событий в единицу времени) постоянна.

2. Поток событий называется потоком без последствия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой (или другие, если рассматривается больше двух участков). Отсутствие последствия в потоке означает, что события, образующие поток, появляются в последовательные моменты времени независимо друг от друга.

3. Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебрежительно мала по сравнению с вероятностью попадания одного события (события в потоке приходят поодиночке, а не парами, тройками и т.д.).

Поток событий, обладающий всеми тремя свойствами, называется простейшим (или стационарным пуассоновским). Нестационарный пуассоновский поток обладает только свойствами 2 и 3. Пуассоновский поток событий (как стационарный, так и нестационарный) тесно связан с известным распределением Пуассона. А именно, число событий потока, попадающих на любой участок, распределено по закону Пуассона. Поясним это подробнее.

Предельные вероятности состояний.

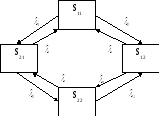
Пусть имеется физическая система S={S₁, S₂, ..., S_n}, в которой протекает марковский случайный процесс с непрерывным временем (непрерывная цепь Маркова). Предположим, что _ij=const, т.е. все потоки событий простейшие

t=0 p₁₁=1 p₂₁=p₂₂=p₁₂=0

p₁₁+p₁₂+p₂₁+p₂₂=1.

(стационарные пуассоновские). Записав систему дифференциальных уравнений Колмогорова для вероятностей состояний и проинтегрировав эти уравнения при заданных начальных условиях, мы получим p₁(t), p₂(t), ..., p_n(t), при любом t. Поставим следующий вопрос, что будет происходить с системой S при t. Будут ли функции p_i(t) стремиться к каким-то пределам? Эти пределы, если они существуют, называются предельными вероятностями состояний. Можно доказать теорему: если число состояний S конечно и из каждого состояния можно перейти (за то или иное число шагов) в каждое другое, то предельные вероятности состояний существуют и не зависят от начального состояния системы. Предположим, что поставленное условие выполнено и предельные вероятности существуют (i=1,2,…n), .

Таким образом, при t в системе S устанавливается некоторый предельный стационарный режим. Смысл этой вероятности: она представляет собой не что иное, как среднее относительное время пребывания системы в данном состоянии. Для вычисления p_i в системе уравнений Колмогорова, описывающих вероятности состояний, нужно положить все левые части (производные) равными 0. Систему получающихся линейных алгебраических уравнений надо решать совместно с уравнением