Рекомендации к выполнению задания

При выполнении пунктов 1–6 задания используется аппарат векторной алгебры, решение пунктов

7–10 основано на применении уравнений прямой и плоскости в пространстве.

Пример решения задачи

Д

аны координаты вершин пирамиды:

А₁ (2, 4, –3),

А₂ (5, 6, 3),

А₃ (–2,7,–3),

А₄ (4, 1, 0).

Решение:

Найдем длину ребра А₁А₂ как модуль вектора:

={x₂ – x₁, y₂ – y₁, z₂ – z₁} =

= {5 – 2, 6 – 4, 3 – (–3)} = {3; 2; 6}

.

Угол между ребрами А₁А₂ и А₁А₄ найдем как угол между векторами = {3; 2; 6} и = {4 – 2, 1 – 4, 0 – (–3)} = {2, –3, 3}, используя скалярное произведение векторов:

( , ) = arccos 0,5482 = 5646.

3. Проекцию ребра А₁А₃ на ребро А₁А₂ найдем как проекцию вектора на вектор :

4. Площадь грани А₁А₂А₃ можно вычислить, используя геометрический смысл векторного произведения векторов (см. пункт в) справочного материала). Найдем векторное произведение векторов

и = :

и его модуль:

.

Модуль векторного произведения векторов равен площади параллелограмма, построенного на векторах и как на сторонах, а площадь грани А₁А₂А₃ составляет половину площади этого параллелограмма, т.е.

(кв. ед.).

5. Длину высоты грани А₁А₂А₃, опущенной из вершины А₃ на ребро А₁А₂ , найдем по формуле

6. Объем пирамиды А₁А₂А₃А₄ можно вычислить, используя геометрический смысл смешанного произведения векторов (см. пункт г) справочного материала). Найдем смешанное произведение векторов = {3; 2; 6}, = {–4, 3, 0} = {2, –3, 3}:

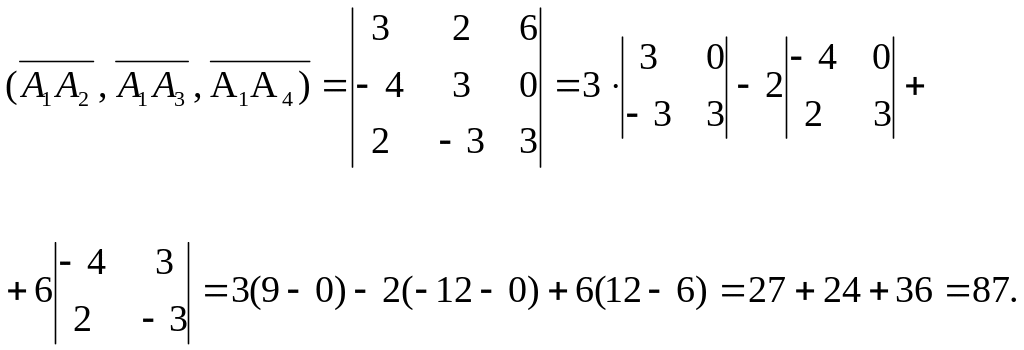
Модуль смешанного произведения векторов ( , , ) равен объему параллелепипеда, построенного на векторах , , как на сторонах, а объем пирамиды А₁А₂А₃А₄ составляет шестую часть объема этого параллелепипеда, т.е.

(куб. ед.).

7. Для составления уравнения прямой А₁А₃ воспользуемся уравнением (5) прямой, проходящей через две данные точки А₁(2,4,–3) и А₃(–2, 7, –3).

или

А₁А₃: .

8. Составим уравнение плоскости А₁А₂А₃. Поскольку плоскость П проходит через три точки

А₁(2, 4, –3), А₂(5, 6, 3), А₃(–2, 7, –3), то согласно (2) получим:

= –18(x – 2) – 24(у -4) + 17(z + 3) = 0

или

18х + 24у – 17z –183 = 0.

9. Угол между ребром А₁А₄ и гранью А₁А₂А₃ найдем по формуле (6) как угол между прямой А₁А₄ и плоскостью П. Направляющий вектор прямой А₁А₄ есть вектор = {2, –3, 3} (см. пункт 4), нормальный вектор плоскости А₁А₂А₃ согласно (1) = {18, 24, –17} (см. пункт 6).

Тогда:

 = arcsin arcsin 0,5379  3233.

10. Составим уравнение высоты h, опущенной на грань А₁А₂А₃ из вершины А₄. Известны координаты точки А₄(4, 1, 0), через которую проходит эта прямая, искомая прямая имеет направляющий вектор , параллельный нормальному вектору = {18, 24, –17} плоскости П грани А₁А₂А₃. Тогда согласно (4) канонические уравнения искомой прямой:

.

Значение h по формуле (3) будет равно

.

Ответ:

1) = 7; 2) 5646;

3) 4) (кв. ед.); 5)

6) (куб. ед.); 7) А₁А₃ : ;

8) П : 18х + 24у + 17z – 183 = 0; 9) 3233;

10) .