
- •Аналитическая геометрия. Содержание:
- •Векторная алгебра
- •Задачи для самостоятельной работы
- •Аналитическая геометрия
- •2.1. Прямая на плоскости
- •Задачи для самостоятельной работы
- •2.2. Прямая и плоскость в пространстве. Различные виды задания уравнений плоскости в пространстве. Прямая в пространстве. Взаимное расположение плоскостей Плоскость в пространстве
- •Прямая в пространстве
- •Задачи для самостоятельной работы
- •2.3. Канонические уравнения кривых 2-го порядка (эллипс, гипербола, парабола)
- •Задачи для самостоятельной работы
- •2.4. Взаимное расположение кривых и прямых на плоскости Задачи для самостоятельной работы
- •2.5. Поверхности второго порядка
- •Задачи для самостоятельной работы
- •Задачи для контрольных заданий
- •1. Задание по теме «Векторы. Линейные операции над векторами»
- •2. Задание по теме «Прямая на плоскости»
- •3. Задание по теме «Кривые второго порядка» Вариант 1.
- •Вариант 2.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15.
- •Вариант 16.
- •Вариант 17.
- •Вариант 18.
- •Вариант 26.
- •Вариант 27.
- •Вариант 28.
- •Вариант 29.
- •Вариант 30.
- •4. Задание по теме «Прямая и плоскость в пространстве»
- •5. Задание по теме «Поверхности второго порядка»
- •Литература Основная
- •Дополнительная
Задачи для самостоятельной работы
22. Написать уравнение прямой, проходящей через точку М0(4;6) и отсекающей от осей координат треугольник площадью, равной 6 кв. ед.
23.
Показать, что прямые
![]() и
и![]() перпендикулярны.
перпендикулярны.
24.
Определить острый угол между прямыми
![]() ,
,
![]() .
.
25.
Определить расстояние между параллельными
прямыми
![]() и
и
![]() .
.
26.
Найти длину высоты
![]() в треугольнике с вершинами
в треугольнике с вершинами
![]() ,
,
![]() и
и
![]() .
.
27.*
Даны стороны треугольника
![]() :
:
![]() ,
,
![]() :
:
![]() ,
,
![]() :
:
![]() .
Найти длину высоты, проведённой из
вершины
.
Найти длину высоты, проведённой из
вершины
![]() .
.
28.*
Даны вершины треугольника:
![]() ,
,
![]() ,
и
,
и
![]() .
Составить уравнение биссектрисы угла
.
Составить уравнение биссектрисы угла
![]() .
.
29.*
Составить уравнение гипотенузы
прямоугольного треугольника, проходящей
через точку
![]() ,
если катеты треугольника расположены
на осях координат, а площадь треугольника
равна 12 ед2.
,
если катеты треугольника расположены
на осях координат, а площадь треугольника
равна 12 ед2.
30.*
Дана вершина треугольника
![]() и уравнения медиан:
и уравнения медиан:
![]() и
и
![]() .
Найти координаты двух других вершин.
.
Найти координаты двух других вершин.
31.*
Даны две противоположные вершины
квадрата
![]() и
и
![]() .
Найти координаты двух его вершин и
написать уравнения его сторон.
.
Найти координаты двух его вершин и
написать уравнения его сторон.
2.2. Прямая и плоскость в пространстве. Различные виды задания уравнений плоскости в пространстве. Прямая в пространстве. Взаимное расположение плоскостей Плоскость в пространстве
Определение 2.2.1.
Всякое
уравнение
![]() первой
степени относительно координат x,
y, z задает
плоскость, и наоборот: всякая плоскость
может быть представлена уравнением,
которое называется уравнением
плоскости.
первой
степени относительно координат x,
y, z задает
плоскость, и наоборот: всякая плоскость
может быть представлена уравнением,
которое называется уравнением
плоскости.
1) Общее уравнение плоскости P имеет вид
![]() (2.2)
(2.2)
В уравнении коэффициенты A, B, C одновременно не равны 0.
Определение 2.2.2.
Вектор
![]() ,
ортогональный плоскости, называется
нормальным
вектором
плоскости.
,
ортогональный плоскости, называется
нормальным
вектором
плоскости.
2) Особые случаи уравнения (2.2):
1.
![]() -
плоскость проходит через начало
координат.
-
плоскость проходит через начало
координат.
2.
![]() - плоскость параллельна оси Oz.
- плоскость параллельна оси Oz.
3.
![]() - плоскость проходит через ось Oz.
- плоскость проходит через ось Oz.
4.
![]() - плоскость параллельна плоскости Oyz.
- плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
3) Уравнение плоскости в «отрезках»
Если
![]() ,
то после преобразования общего уравнения
имеем
,
то после преобразования общего уравнения
имеем
![]() ,
где a,
b,
с –
соответственно абсцисса, ордината и
аппликата точек пересечения прямой с
осями Ox,
Oy
и Oz.
,
где a,
b,
с –
соответственно абсцисса, ордината и
аппликата точек пересечения прямой с
осями Ox,
Oy
и Oz.
4) Уравнение плоскости, проходящей через три заданные точки Уравнение плоскости, проходящей через три заданные точки M(x1;y1;z1), M(x2;y2;z2), M(x3;y3;z3), имеет вид

5) Угол между двумя плоскостями
Угол
между двумя плоскостями, имеющими
нормальные векторы
![]() и
и
![]() ,
определяется как угол между данными
нормальными векторами; косинус этого
угла находится по формуле
,
определяется как угол между данными
нормальными векторами; косинус этого
угла находится по формуле

6) Условие параллельности плоскостей
Условие
параллельности плоскостей
![]() и
и
![]()
![]()
7) Условие совпадения двух плоскостей
Плоскости
P1
и P2
совпадают,
если
![]() .
.
8) Условие перпендикулярности плоскостей
Условие перпендикулярности плоскостей P1 и P2
![]() .
.
9) Уравнение плоскости, проходящей через точку M(x0;y0;z0) перпендикулярно вектору
![]()
10) Расстояние от точки до плоскости
Расстояние d от заданной точки M(x0;y0;z0) до заданной прямой с уравнением определяется по формуле
![]() .
.
Прямая в пространстве
Прямая в пространстве может быть задана:
1) Как пересечение двух плоскостей
Прямую l можно задать как пересечение двух плоскостей
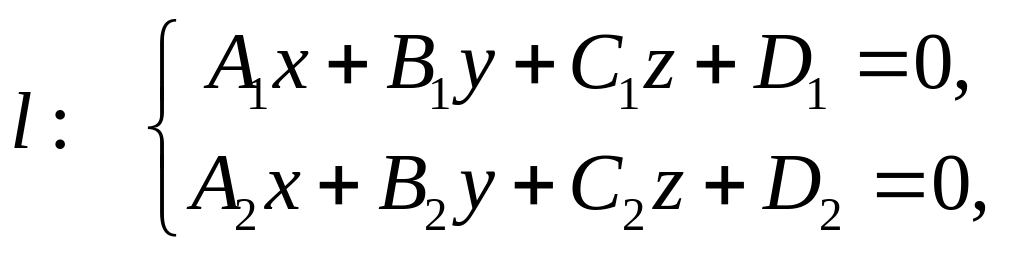
тогда ее направляющий вектор будет равен

2) Уравнение прямой, проходящей через две точки
Уравнение прямой можно задать двумя точками M1(x1,y1,z1) и M2(x2,y2,z2), тогда прямая, через них проходящая, задается уравнениями:
![]()
3) Канонические уравнения прямой
Уравнение
прямой можно задать точкой M1(x1,y1,z1),
ей принадлежащей, и вектором
![]() ,
ей коллинеарным. Тогда прямая определяется
уравнениями:
,
ей коллинеарным. Тогда прямая определяется
уравнениями:
![]()
Данные уравнения называются каноническими уравнениями прямой, а вектор - направляющий вектор прямой.
4) Параметрические уравнения прямой
Рассмотрим канонические уравнения прямой и введем параметр t
![]() .
Тогда получим систему, которая дает
параметрические уравнения прямой на
плоскости
.
Тогда получим систему, которая дает
параметрические уравнения прямой на
плоскости
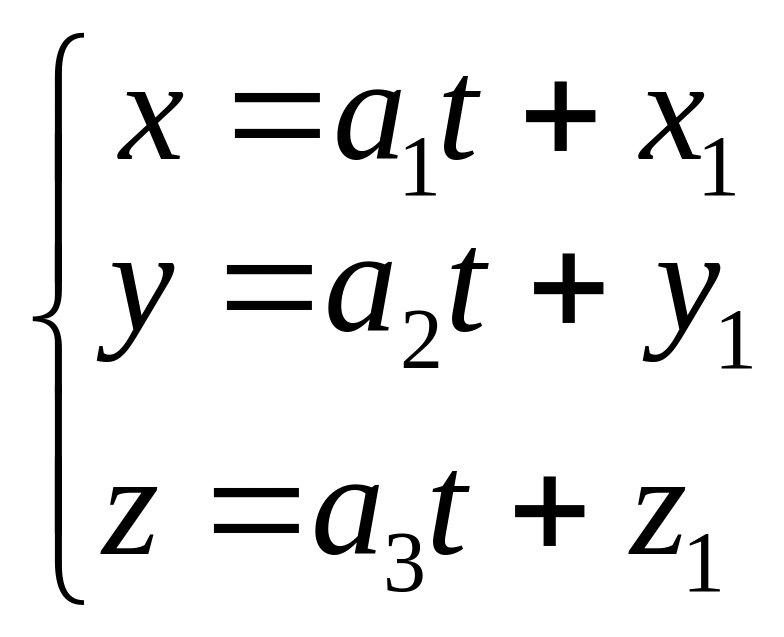
5) Угол между двумя прямыми
Угол
φ между прямыми, заданными каноническими
уравнениями
![]() и
и
![]() определяется из соотношения
определяется из соотношения
 .
.
6) Условие параллельности прямых
Если
прямые заданы каноническими уравнениями
и
,
то они параллельны
в случае
![]() .
.
7) Условие перпендикулярности прямых
Если
прямые заданы каноническими уравнениями
и
,
то они перпендикулярны в случае
![]() .
.
8) Условие компланарности двух прямых
Если
прямые заданы каноническими уравнениями
и
,
то они компланарны в случае

Замечание. Прямые компланарны, если существует плоскость, которой они параллельны.
9) Угол между прямой и плоскостью
Если прямая задана каноническими уравнениями , а плоскость задана общим уравнением , то угол между ними определяется по формуле

10) Условие параллельности прямой и плоскости
Если
прямая задана каноническими уравнениями
,
а плоскость задана общим уравнением
,
то они параллельны, если выполняется
![]() .
.
11) Условие перпендикулярности прямой и плоскости
Если
прямая задана каноническими уравнениями
,
а плоскость задана общим уравнением
,
то они перпендикулярны, если выполняется
![]() .
.
12) Точка пересечения прямой и плоскости
Чтобы определить точку пересечения прямой, заданной каноническими уравнениями и плоскости, заданной общим уравнением , нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой , которые необходимо подставить в уравнение плоскости. Получим уравнение с неизвестным параметром t. Найденный параметр подставим в параметрические уравнения и получим координаты искомой точки.
Возможны варианты:
а)
если
![]() ,
то прямая пересекает плоскость;
,
то прямая пересекает плоскость;
б)
если
и
![]() ,
то прямая параллельна плоскости;
,
то прямая параллельна плоскости;
в)
если
и
![]() ,
то прямая лежит в плоскости.
,
то прямая лежит в плоскости.
Пример 2.3. Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение. По условию задачи вектор ОА(1,-1,3) является нормальным вектором плоскости, тогда ее уравнение можно записать в виде
x-y+3z+D=0.
Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 1-(-1)+3×3+D = 0 , D = -11. Итак, x-y+3z-11=0.
Пример 2.4. Составьте уравнение плоскости, проходящей через ось Оz и образующей с плоскостью 2x+y-z-7=0 угол 60о.
Решение. Плоскость, проходящая через ось Oz, задается уравнением Ax+By=0, где А и В одновременно не обращаются в нуль. Пусть В не равно 0, A/Bx+y=0. По формуле косинуса угла между двумя плоскостями
![]() ,
где m=A/B.
,
где m=A/B.
Решая квадратное уравнение 3m2 + 8m - 3 = 0, находим его корни
m1 = 1/3, m2 = -3, откуда получаем две плоскости
1/3x+y = 0 и -3x+y = 0.
Пример 2.5. Составьте канонические уравнения прямой:
5x + y + z = 0, 2x + 3y - 2z + 5 = 0.
Решение. Канонические уравнения прямой имеют вид:
![]()
где
![]() -
координаты направляющего вектора
прямой, x1,
y1,
z1
- координаты какой-либо точки, принадлежащей
прямой. Прямая задана как линия пересечения
двух плоскостей. Чтобы найти точку,
принадлежащую прямой, фиксируют одну
из координат (проще всего положить,
например, x=0)
и полученную систему решают как систему
линейных уравнений с двумя неизвестными.
Итак, пусть x=0,
тогда y + z =
0, 3y - 2z+ 5 = 0,
откуда y=-1,
z=1. Координаты
точки М(x1,
y1,
z1),
принадлежащей данной прямой, мы нашли:
-
координаты направляющего вектора
прямой, x1,
y1,
z1
- координаты какой-либо точки, принадлежащей
прямой. Прямая задана как линия пересечения
двух плоскостей. Чтобы найти точку,
принадлежащую прямой, фиксируют одну
из координат (проще всего положить,
например, x=0)
и полученную систему решают как систему
линейных уравнений с двумя неизвестными.
Итак, пусть x=0,
тогда y + z =
0, 3y - 2z+ 5 = 0,
откуда y=-1,
z=1. Координаты
точки М(x1,
y1,
z1),
принадлежащей данной прямой, мы нашли:
M (0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей a1(5,1,1) и a2(2,3,-2). Тогда

Канонические
уравнения прямой имеют вид:
![]() .
.
Пример 2.6. В пучке, определяемом плоскостями 2х-у+5z-3=0 и х+у+2z+1=0, найти две перпендикулярные плоскости, одна из которых проходит через точку М(1,0,1).
Решение. Уравнение пучка, определяемого данными плоскостями, имеет вид u(2х-у+5z-3) + v(х+у+2z+1)=0, где u и v не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом:
(2u +v)x + (- u + v)y + (5u +2v)z - 3u + v = 0.
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
(2u+v)×1 + ( -u + v)×0 + (5u + 2v )×1 -3u + v =0, или v = - u.
Тогда уравнение плоскости, содержащей M, найдем, подставив v = - u в уравнение пучка:
u(2x-y +5z - 3) - u (x + y +2z +1) = 0.
Т.к. u¹0 (иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости x-2y+3z-4=0. Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей:
(2u+ v)×1 + (v - u)×(-2) + (5u +2v)×3 = 0, или v = - 19/5u.
Значит, уравнение второй плоскости имеет вид:
u(2x -y+5z - 3) - 19/5 u(x + y +2z +1) = 0 или 9x +24y + 13z + 34 = 0.
