3.2.3 Геометричні співвідношення для антени Кассегрена

На рис.13,а показана геометрія антени Кассегрена, а на рис.13,б - фрагмент її побудови. На малюнку позначено: - половина кутової апертури основного дзеркала; - половина кутової

апертури допоміжного дзеркала; F - фокусні відстані параболоїда і гіперболоїда відповідно.

Для гіперболоїда справедливі наступні рівності:

Ексцентриситет утворюючої гіперболи

Для одержання плоского фронту хвилі на вихід антени (наприклад, у площині ) необхідно, щоб оптична довжина променів для всіх була постійною.

Використовуючи (38), (39,б) і основну властивість параболи

знаходимо, що

Із приведеної геометрії антени можна одержати цілий ряд співвідношень, що необхідні для розрахунку антени:

Основні характеристики антени Кассегрена визначаються кількісно двома методами: методом мнимого опромінювача і методом еквівалентної параболи.

У першому методі реальний опромінювач і допоміжне дзеркало заміняються мнимим опромінювачем, розташованим у фокусі основного дзеркала. При цьому задача аналізу антени Кассегрена зводиться до аналізу однодзеркальної антени, що має таке ж дзеркало, як і основне в розглянутій системі, але інший опромінювач.

Метод еквівалентної параболи має деякі переваги перед методом мнимого опромінювача при аналізі характеристик випромінювання антен. При даному методі задача проектування антени зводиться до створення однодзеркальної системи, що має той же опромінювач, що й у реальної антені, але інше основне (велике) дзеркало.

Еквівалентне дзеркало також є параболоїдом обертання з фокусною відстанню і являє собою геометричне місце точок перетинання променів, що виходять з реального опромінювача О з відповідними променями, що перетерпіли відображення від допоміжного й основного дзеркал. При цьому діаметри розкриву еквівалентного і реального основного дзеркал однакові. Геометрія побудови еквівалентного дзеркала показана на рис.14.

Рівняння, що визначає еквівалентну параболу, наступне:

де - значення кутів у межах кутової апертури; - для основного дзеркала; - відповідне значення кутів у межах апертури еквівалентного дзеркала.

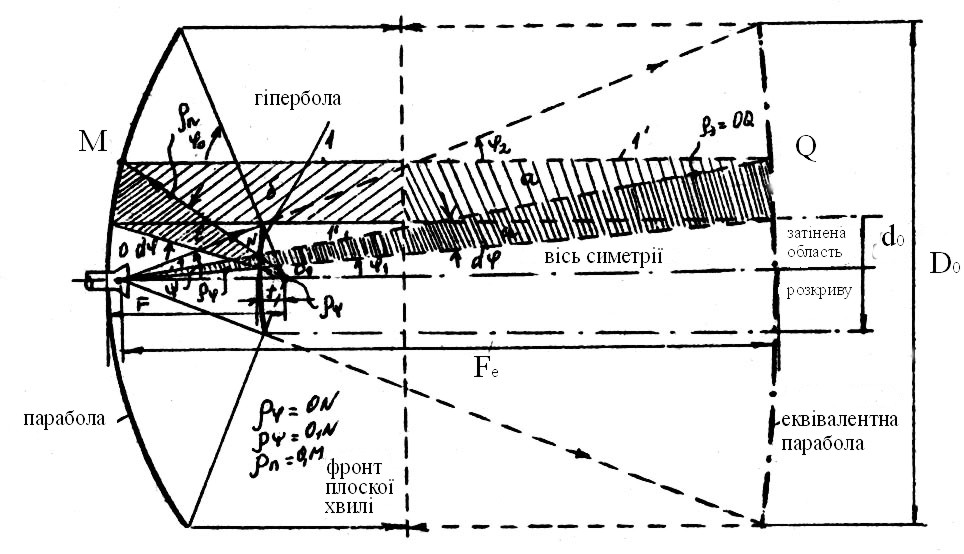
Рисунок 14 – Побудова еквівалентної параболи

Рівняння тієї ж кривої можна представити в іншому виді з урахуванням співвідношення між кутами і :

це і дозволить отримати після ряду перетворень

де (50)

( - ексцентриситет гіперболи).

Рівняння (49) описує параболу з фокусною відстанню Побудована таким чином парабола є утворюючою кривої еквівалентного параболоїда. В відповідності з (50) еквівалентна парабола завжди є більш довгофокусною, чим вихідна парабола. Формули, що дозволяють розрахувати геометрію антени, наступні:

На рис.15 зображені графічні залежності різних конструктивних параметрів, необхідних для проектування антени.

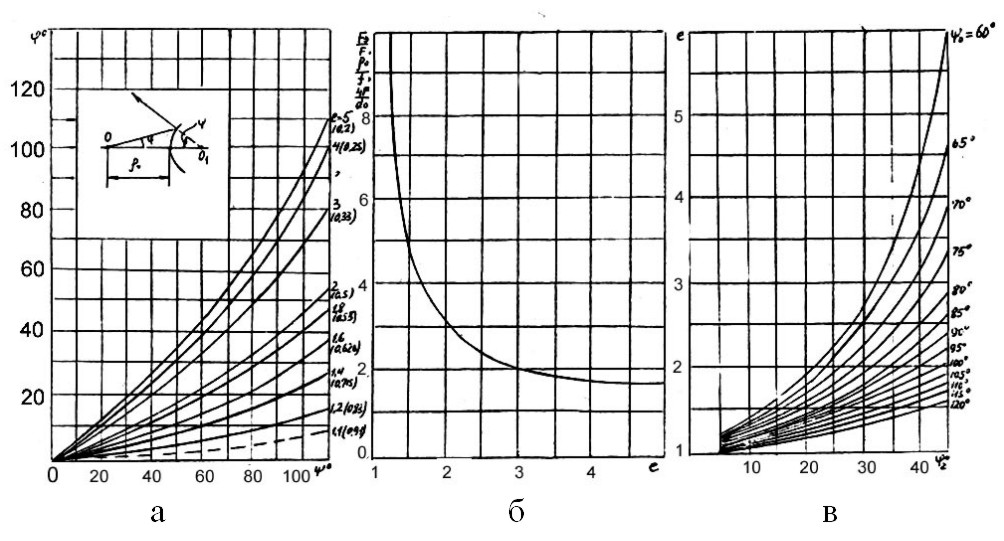
Рисунок 15 (а) Співвідношення між кутами, (б) співвідношення між лінійними розмірами та ексцентриситетом, (в) залежність між кутами та ексцентриситетом

Найбільш уживані значення ексцентриситету лежать у межах 1,2...2.

3.2.4 Визначення розмірів основного і допоміжного дзеркал

Діаметр великого дзеркала визначається з необхідного КСД як діаметр апертури антени. При цьому необхідно врахувати, що сумарний КВП апертури лежить у межах 0,6...0,7.

Для круглих апертур площа апертури

звідки і знаходимо .

Оскільки основним недоліком дводзеркальних антен є наявність затінення структури малим дзеркалом, необхідно мінімізувати його розміри. Однак зменшення розмірів малого дзеркала потребуватиме звуження діаграми спрямованості опромінювача, що у свою чергу приведе до збільшення габаритних розмірів апертури опромінювача. Тому оптимальною необхідно вважати ситуацію, за якої діаметр малого дзеркала буде дорівнювати розміру затінення ( ), як це вказано на рис.16.

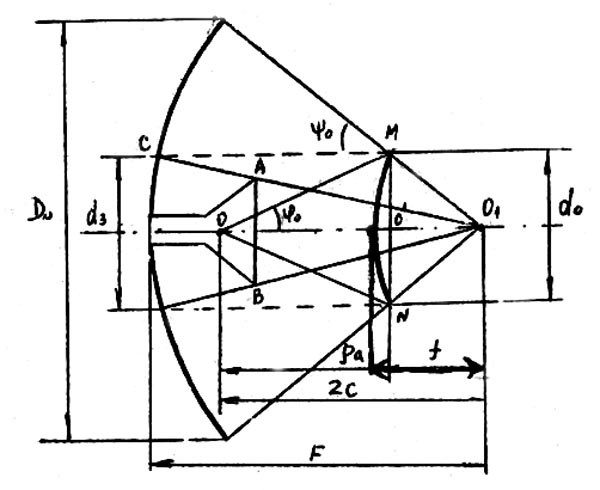
Рисунок 16 – До визначення геометричних розмірів антени Касегрена

Позначимо розмір апертури опромінювача і з урахуванням подоби трикутників і одержимо

З іншого боку, із трикутника , маємо

З урахуванням прийнятих позначень запишемо

Підставляючи (62) у (61), одержуємо

Оскільки задача розв’язується в припущенні, що ,

маємо

і після обчислення квадратного кореня одержуємо .

З отриманих співвідношень (61) і (64) можна знайти відстань

Розрахунки й експерименти показали, що якщо діаметр малого дзеркала брати не більш 0,25 , то падіння коефіцієнта підсилення і ріст бічних пелюстків не занадто великі (КСД знижується приблизно на 10%, а бічний пелюсток збільшується на 1,5%).

У практичних конструкціях значення вибирається в межах (0,15...0,25) .

Що стосується вибору фокусних відстаней, то для геометрії антен Кассегрена характерні наступні співвідношення:

При цьому рівняння кривої другого порядку малого дзеркала, описане в полярних координатах щодо ближнього фокуса , має вид

У залежності від значення ексцентриситету рівняння описує наступні криві:

- окружність;

- сімейство еліпсів;

- сімейство гіпербол;

- пряму .

Рівняння тієї ж кривої, записане щодо далекого фокуса , має вид

Відстань від вершини кривої (малого дзеркала) до далекого фокуса ;

При цьому звертаємо увагу на співвідношення