4. Коинтеграция в динамических системах: подход Йохансена

Наряду с подходом Грейнджера популярен и другой метод нахождения стационарных комбинаций — метод Йохансена. Он может использоваться для тестирования стационарности найденных линейных комбинаций и распространяет методику Дики-Фуллера на случай векторной авторегрессии. Причем если в обычной авторегрессии рассматривался один коэффициент автокорреляции ρ, то здесь следует рассматривать уже матрицу коэффициентов. Предполагается (как и в ADF), что если добавить достаточное число лагов в авторегрессионную модель, то ошибка не будет сериально коррелированной.

Если векторный процесс состоит более чем из двух процессов (S>2), то может существовать несколько коинтегрирующих векторов. Если существует ровно r линейно независимых коинтегрирующих векторов, то говорят, что ранг коинтеграции равен r.

Обозначим через β матрицу, составленную из таких векторов. Набор коинтегрирующих векторов не является однозначным, на самом деле речь должна идти о коинтеграционном пространстве. Нормировку следует выбирать исходя из экономической теории рассматриваемых процессов.

Метод Йохансена позволяет не только найти матрицу коинтеграционных векторов при данном ранге коинтеграции, но и проверять гипотезы о ранге коинтеграции (количестве коинтегрирующих векторов). Метод непосредственно работает с векторной моделью исправления ошибок.

Пусть Y_t = (Y_1t, ..., Y_nt) — векторный процесс (вектор-строка), каждая из компонент которого является I(1) (или I(0)). Порождающий данные процесс задается формулой:

.

Предполагается, что ошибки, относящиеся к разным моментам времени,

независимы, и ε_t~ N(0,Ω). В модели оцениваются вектор-строка констант μ₀ и коэффициентов при трендах μ₁, матрицы коэффициентов Γ₁,..., Γ_L–1 и Π размерности (n×n), а также ковариационная матрица Ω. Поскольку по предположению ΔY_t~I(0), то должно быть выполнено . Ограничения на ранг коинтеграции задаются как ограничения на матрицу Π. При нулевой гипотезе, что ранг коинтеграции равен r, ее можно представить в виде

,

где матрицы α и β имеют размерность (n×r); β — матрица коинтегрирующих векторов, α — матрица корректирующих коэффициентов. Если r = 0, то Π = 0 и не существует стационарных линейных комбинаций переменных Y_1t, ..., Y_nt.

В другом крайнем случае, когда n = r любая линейная комбинация этих переменных стационарна, то есть все они I(0).

Для оценивания модели используется метод максимального правдоподобия. При данной матрице β можно получить оценки максимального правдоподобия для остальных неизвестных параметров обычным методом наименьших квадратов. Йохансен показал также, что максимизация функции правдоподобия по β эквивалентна задаче отыскания собственных чисел для некоторой симметричной положительно определенной матрицы. При ранге коинтеграции r выбираются r минимальных собственных чисел. Если расположить собственные числа в порядке возрастания (λ1≤ λ2≤ ... ≤ λn), то следует

выбрать λ1, λ2, ..., λr. (Йохансен записал ПДП в несколько ином виде, и поэтому у него собственные числа идут в порядке убывания и выбираются r максимальных собственных чисел.) Столбцами матрицы β (коинтегрирующими векторами) будут соответствующие собственные вектора. Конечно, β определяется только с точностью до некоторой нормировки. После того, как найдена оценка максимального правдоподобия , вычисляются оценки других параметров.

Для проверки гипотез об r используется статистика отношения правдоподобия. Статистика следа используется для проверки гипотезы (H₀) о том, что ранг равен r, против гипотезы (H_A) о том, что ранг равен n. Статистика имеет вид

Тестирование проводится последовательно для r = n–1,...,0 и заканчивается, когда нулевая гипотеза не будет отвергнута в первый раз. Можно проводить тестирование в обратном порядке r = 0,..., n–1. В этом случае тестирование заканчивается, когда нулевая гипотеза будет отвергнута в первый раз.

Можно также использовать статистику максимального собственного числа, которая используется для проверки гипотезы (H₀) о том, что ранг равен r, против гипотезы (H_A) о том, что ранг равен r +1. Эта статистика есть

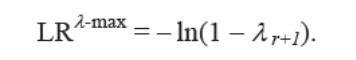
Обе указанные статистики имеют нестандартные асимптотические распределения, зависящие только от n – r и уточняются включением в модель константы и тренда.

Метод Йохансена можно использовать также для оценивания моделей с линейными ограничениями на матрицу коинтегрирующих векторов β и на матрицу корректирующих коэффициентов α. Для проверки таких ограничений предлагается использовать все тот же тест отношения правдоподобия, который здесь имеет обычное асимптотическое распределение