3. Приклад виконання завдання к1

Вихідні дані: x(t)=3cos y(t)= 4sin см, t₁=1 c, t₂=2 c.

1 Визначаємо рівняння траєкторії в явній формі:

, слід., -траєкторія- еліпс.

2 Будуємо траєкторію точки на інтервалі часу 0 – 2 с (рис.1.3).

3 Позначимо положення точки при t=1 c (x(1)=2,6, y(1)=4).

4 Визначаємо проекції вектора швидкості: . При t=1с v_x=-0,785, v_y=1,815 см/с. Величина швидкості см/с,

5 Будуємо на рисунку вектор швидкості .

6 Визначаємо проекції вектора прискорення і будуємо вектор :

.

При t=1c а_х=-0,713 см/с², а_у=-0,548 см/с², а= =0,899 см/с².

7 Обчислюємо дотичне прискорення при t=1c

y = -0,204 см/с²

v_y 8 Обчислюємо нормальне приско-

a_x v_x рення: =0,875 см/с²

t=1 9 Визначаємо радіус кривизни тра-

єкторії при t=1c:

C a_y 5,185 см.

__________________________

x Обчислювання координат точки:

t c	0	1	1.5	2
x(t)	3	2.59	2.12	1.5
y(t)	2	4	4.83	5.46

Рис.1.3

Тема 2 обертальний рух твердого тіла

2.1 Загальні вказівки

Положення у просторі тіла, що обертається навколо нерухомої осі, визначається кутом повороту , який задається як функція часу (рівняння обертального руху).

За відомим кутом обертання можна визначити кутову швидкість та кутове прискорення тіла: .

Швидкість точки тіла, яка розташована на відстані h від осі обертання, виз- начається за формулою . Звертаємо увагу на те, що швидкість точки ті- ла пропорційна її радіусу, а вектор швидкості завжди перпендикулярний до ра- діуса й спрямований в бік обертання (рис.2.1).

Прискорення точки тіла складається з двох компонентів: обертального а_об=

= та доцентрового а_дц= прискорень. Повне прискорення а= =

= (рис.2.2).

Кут між вектором прискорення і радіусом визначається за допомогою його тангенса: . Кут не залежить від радіуса, він однаковий для всіх точок тіла. Отже, прискорення також пропорційно радіусу. Вектор прискорен- ня нахилений до радіуса на кут .

а_дц

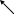
а_об

Рис.2.1 Рис.2.2

2.2. Завдання к2

Вантаж А опускається наниз за законом y=f(t) і приводить в рух шестерню (шків) 1, яка передає обертання шестерні (шківу) 2. Визначити швидкість та прискорення точки М на ободі шестерні 2 в момент часу t₁= 2 с (рис.2.3)

Таблиця 2.1 Варіанти завдання К2

№ вар	№ сх..	f(t) см	r1 см	R1 см	R2 см	№ вар	№ сх	f(t) см	r1 см	R1 см	R2 см
1	1	3t2	5	8	12	16	7	4t5	5	8	16
2	2	5t3	6	8	12	17	8	5t3	5	8	12
3	3	4t5	8	12	14	18	9	3t2	4	r2=5	12
4	4	2t3	10	12	20	19	1	0.1t3	6	8	14
5	5	3t4	12	24	18	20	2	3t4	5	8	16
6	6	0.1t3	3	10	4	21	3	2t3	5	8	10
7	7	0.5t2	4	6	10	22	4	4t3+2t	4	6	12
8	8	8t2	4	6	10	23	5	5t2	6	14	10
9	9	6t4	5	r2=4	10	24	6	3t3	4	10	3
10	1	6t3	4	6	10	25	7	6t2+3t	5	7	14
11	2	8t2	4	7	11	26	8	0.8t3	4	6	8
12	3	0.5t2	4	8	12	27	9	0.5t2	6	r2=7	14
13	4	0.1t3	5	10	16	28	1	0.3t4	5	7	10
14	5	3t4	5	10	8	29	2	0.1t5	5	8	12
15	6	2t3	5	12	4	30	3	2t2	6	10	12