Бульбашкове сортування

Під час обмінного сортування упорядкований список виходить із систематичним обміном сусідніх елементів, що не відповідають необхідному порядку, доки такі пари існують.

Найбільш відомим методом систематичного обміну сусідніх елементів з неправильним порядком є "бульбашкове сортування". У цьому методі здійснюється перегляд всього списку зліва направо, і виробляється взаємозаміна елементів при порушенні закону відповідності. Максимальні елементи як би "спливають" наприкінці списку, що визначило назву методу. Якщо на якомусь проходженні обмінів не було – сортування закінчене.

У наших прикладах будемо вважати, що сортується одномірний масив (або його частина від індексу до індексу ) у порядку зростання елементів. Нижче наводиться приклад програми, що реалізує метод "бульбашкового сортування".

/*сортування бульбашковим методом*/

float * bubble(float * a, int m, int n)

{ char is=1;

int i;

float c;

while(is)

{ is=0;

for (i=m+1; i<=n; i++)

if ( a[i] < a[i-1] )

{ c=a[i];

a[i]=a[i-1];

a[i-1]=c;

is=1;

} } return(a); }

3.3 Варіанти індивідуальних завдань лабораторної роботи 3

Розробити алгоритм і програму формування заданої послідовності відповідно до вашого варіанта і відсортувати її.

При формуванні послідовностей використовувати функції: і т.п.

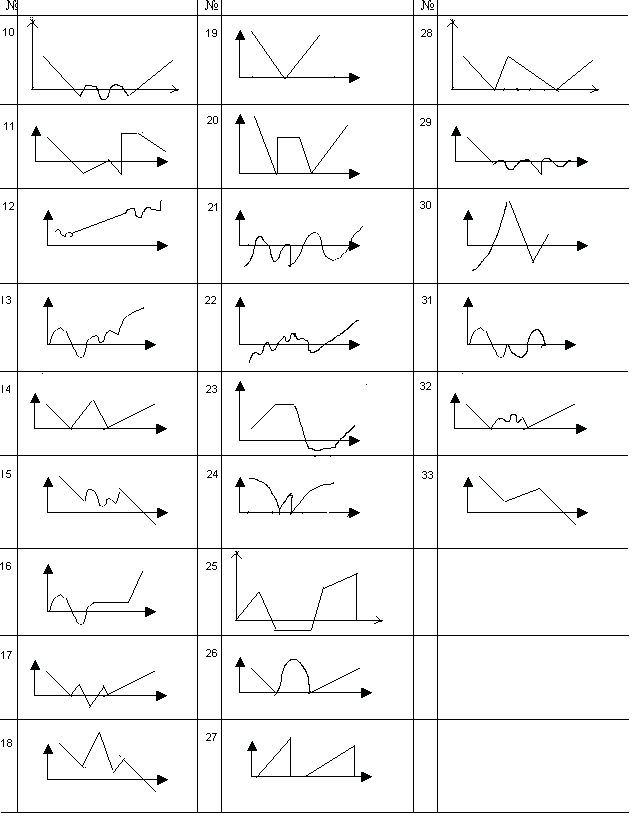
3.4 Контрольні запитання

1. У чому відмінність внутрішнього і зовнішнього сортування даних?

2. Які основні категорії методів сортування Ви знаєте?

3. Які способи оцінки алгоритмів Ви знаєте?

4. Які вимоги можуть висуватися до алгоритмів сортування?

5. Які методи сортування є стійкими?

4 РОЗВ’ЯЗАННЯ ЗАДАЧ З ВИКОРИСТАННЯМ ГРАФІВ ТА ЗНАХОДЖЕННЯ ХРОМАТИЧНОГО ЧИСЛА

4.1 Мета роботи

Одержати практичні навички аналізу графів, використовуючи методи функціонального і логічного програмування.

4.2 Підготовка до роботи

Студент повинен знати основні визначення теорії графів. У даній роботі вивчаються основні поняття теорії графів, на основі яких розглядається задача визначення хроматичного числа графа.

Графом називають сукупність двох множин – множини (вершин графа) і множини (ребер графа) неупорядкованих пар різних елементів множини .

= . .

Часто користуються й іншим визначенням графа. Графом називають упорядковану трійку

,

де – множина вершин графа, – множина ребер графа, – інцидентор – тримісний предикат, що визначає, якій парі вершин відповідає ребро . Це визначення еквівалентне попередньому.

Якщо ,

де , то можна задати у вигляді , тому що інцидентор визначений завданням множин і .

Нехай , – вершини, – з'єднуюче їхнє ребро. У цьому випадку вершина і ребро інцидентні, так само як і з також інцидентні.

Вершини , інцидентні ребрам , якщо і називаються суміжними. Два ребра, інцидентні одній вершині, також називаються суміжними.

Множина вершин , інцидентних з вершиною , називається множиною суміжності вершини і позначається .

, , .

Якщо з випливає, що , то такий граф називається неорієнтованим.

Якщо елементами графа служать упорядковані пари := , то такий граф є орієнтованим. У цьому випадку елементи множини звуться вузлами, а елементи множини – дугами.

Якщо елементом множини може бути пара однакових елементів , то такий елемент множини зветься петлею, а граф – графом з петлями, чи псевдографом.

Дані про граф задаються матрицею суміжності, чи матрицею інцидент- ності.

Матрицю , де і потужності множин і ,відповідно називають матрицею інцидентності графу в тому випадку, коли

1, якщо вершина інцидентна ребру ,

0, якщо вершина неінцидентна ребру

Розфарбуванням неорієнтованого графу зветься таке приписування кольорів (натуральних чисел) його вершинам , де , що ніякі дві суміжні вершини не одержують однаковий колір. Найменша кількість кольорів, що використовуються під час розфарбування, зветься хроматичним числом.

Як приклад, вирішимо задачу розфарбування графу, зображеного на рис. 5.1

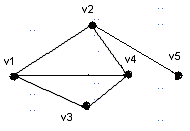
Рисунок 5.1