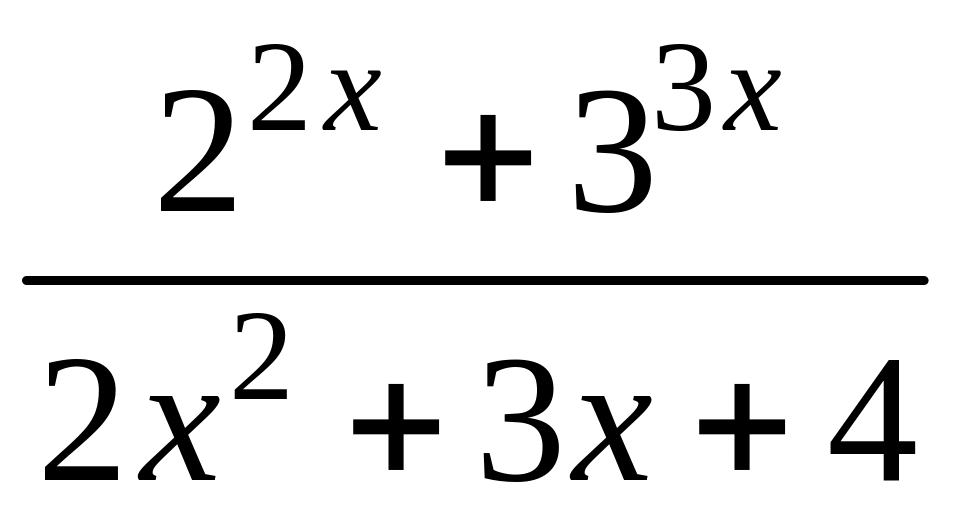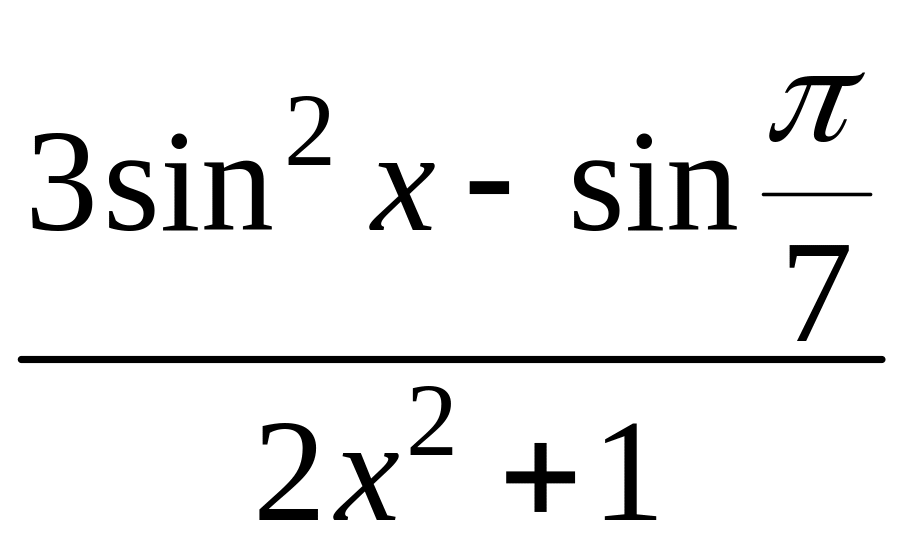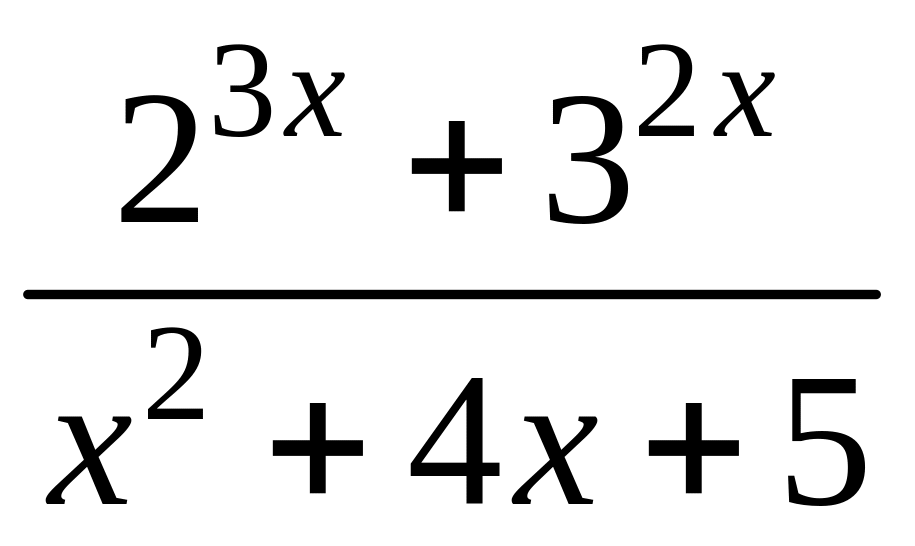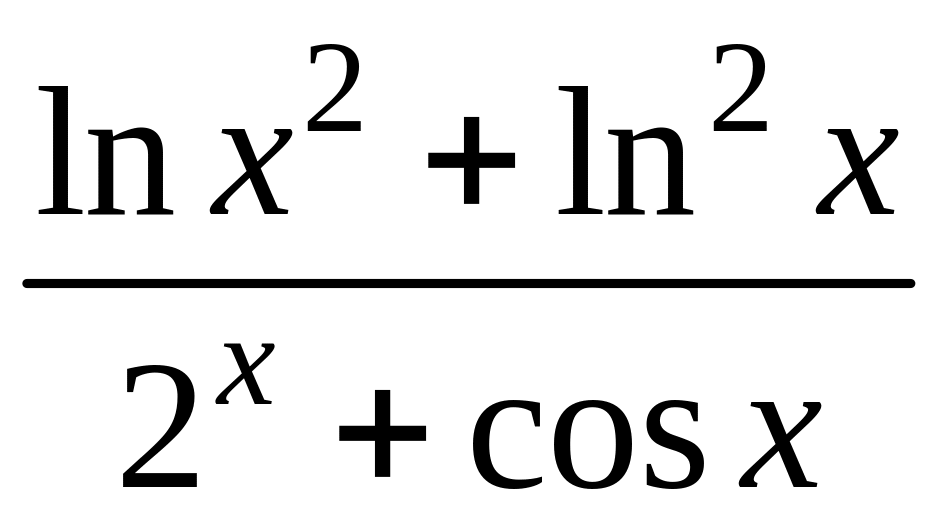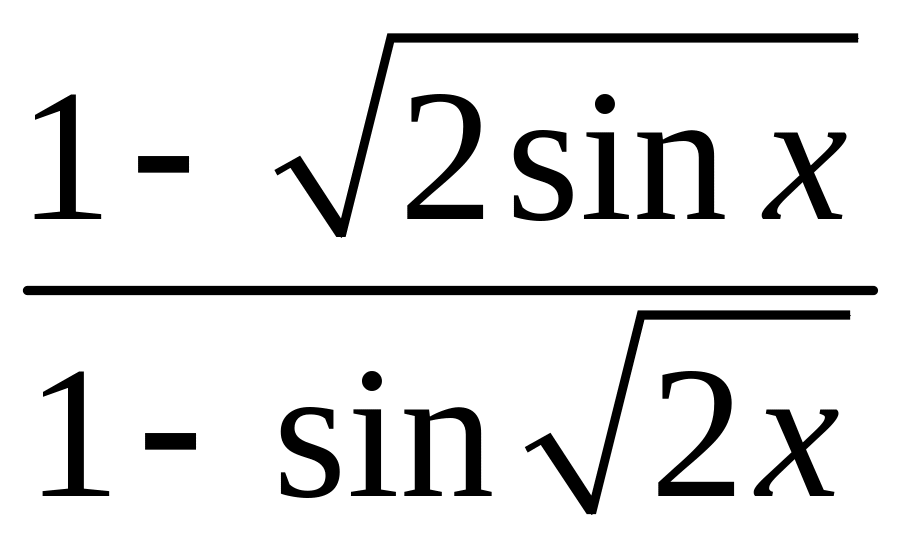Решение типовых примеров

1.20 Известно, что функция , , непрерывна в точке , яв­ляющейся предельной для . Найти , если , , .

Пусть функция определена в точке . Можно ли находить , просто вычисляя значение функции в точке , если из­вестно, что не является непрерывной в точке ?

Решение. Так как функция непрерывна в точке 0, то её пре­дел в этой точке равен значению: = .

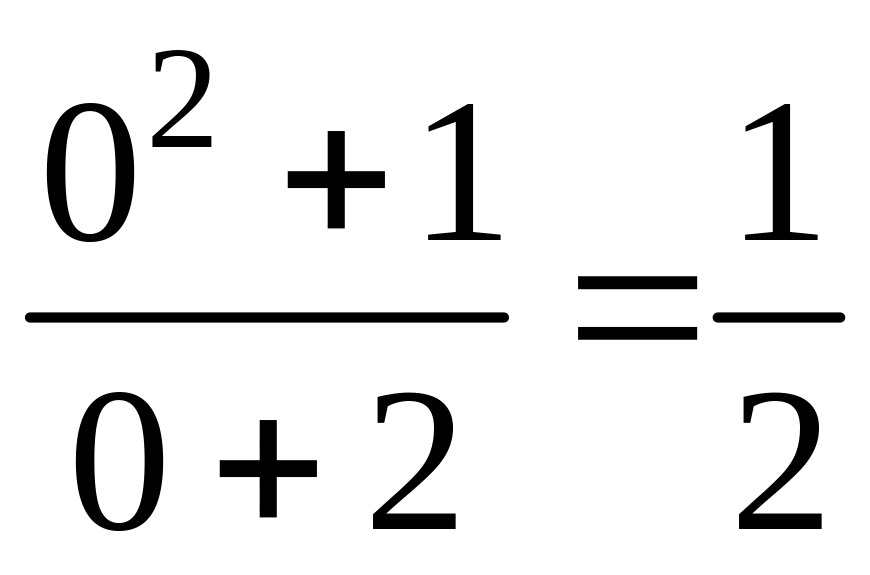Если известно, что не является непрерывной в точке , то  не существует. (Напомним, что в определении предела функ­ции в точке, принятом в [1], сама точка не исключается. Так как функ­ция определена в точке , то из существования предела следовало бы, что = ). Конечно, может существовать, но и в этом случае его нельзя находить, «вычисляя значение функции в точке », так как из разрывности функции в точке следует, что

2.20 Для функции , с областью определения , точки и положи­тельных чисел и найти такие положительные и , что для любых , удовлетворяющих условию , выполняется усло­вие .

Для произвольного положительного найти такое положительное , что для любых , удовлетворяющих условию , выполня­ется условие . Построить график функции и проил­люстрировать геометрически процедуру поиска по заданному . Запи­сать доказанное утверждение, используя понятие предела и понятие не­прерывности функции в точке.

, , , .

Решение. Неравенство равносильно неравен­ству . Если положить , то из сле­дует . Доказанное утверждение означает, что существует (и равен ), иначе говоря, означает, что функция непрерывна в точке (-3). Заметим, что в качестве искомого можно было взять и любое число, меньшее, чем .

3.20 Доказать непрерывность функции , , где в точке непосредственно по определению непрерывности ([1], с. 170) и определению предела функции по Коши ([1], с. 152), если , .

Решение. Согласно определению непрерывности функции в точке ([1], с. 170), надо доказать лишь существование предела . Учитывая, что данная функция определена в точке , из существования предела будет следовать его равенство значению функции в точке . Итак, требуется доказать, что .

Рассмотрим произвольное положительное и будем искать такое поло­жительное , что из неравенства вытекает неравенство . Подчеркнём: нам не требуется доказывать равносильность этих неравенств; достаточно доказать лишь логическое следование .

Неравенство вытекает из неравенства , а это последнее – из высказывания (в самом деле, если , то и, следовательно, и, следовательно, ).

Теперь понятно, какое можно взять . Положим . Тогда

.

4.20 Построить график функции , и график функции , . Доказать непрерывность функции , в точке непосредственно по определению непрерывности ([1], с. 170) и определению предела функции по Коши ([1], с. 152). Является ли не­прерывной в точке функция , ? В обозначении предела и при формулировке утверждений о непрерывности обязательно указывайте область определения функции. , , .

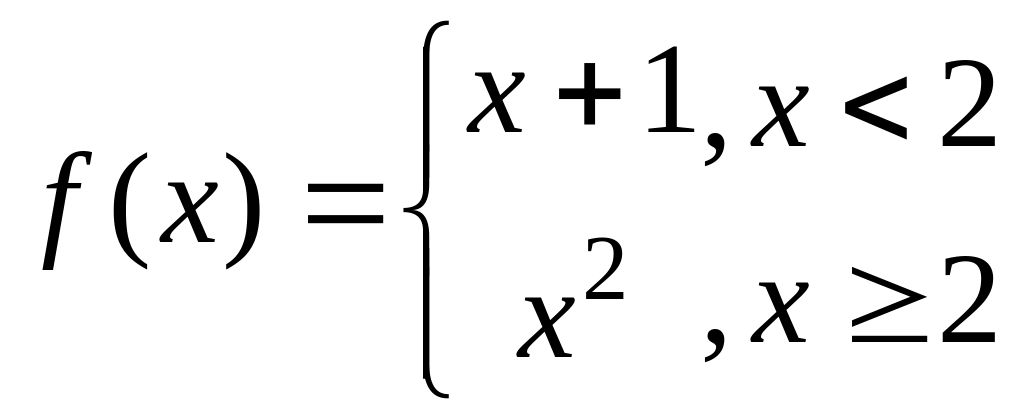Решение. Напомним, что из следует, что и по любому подмножеству множества (для которого – точка прикосновения) пре­дел существует и равен : .

Так как и , то . Так как заданная функция равна функции на , то . Это доказывает непрерывность функции , в точке .

Отметим, что функция , разрывна в точке (если бы существовал и был равен , то и существовал бы и был бы равен , то есть равен ; легко ви­деть, что = = = .

5.20 Для вычисления значения функции в точке значение аргу­мента нашли с некоторой погрешностью . В результате и значе­ние функции оказалось получено с некоторой погрешностью (то есть вме­сто вычислили ; погрешность значения функции равна , она зависит от погрешности аргумента). Для указан­ных функции , и точки доказать, что погреш­ность значения функции может быть сделана сколь угодно малой, если только погрешность аргумента достаточно мала. Точнее, доказать, что для лю­бого положительного существует такое положительное , что для лю­бых , удовлетворяющих условиям и , выпол­ня­ется условие . Сформулировать определение непрерывно­сти функ­ции «на языке приращений». , .

Решение. =

= = . При (то есть при ) бу­дет находиться в пределах от (-2) до 0 и, следовательно,

. Для заданного положительного положим . Ясно, что из (то есть из ) следует . Доказано, что , то есть доказана непрерыв­ность данной функции в данной точке.

6.20. Сформулировать определение непрерывности функции на языке окре­стностей. Построить график функции , . Построить указан­ную окрестность точки и найти (сначала геометриче­ски, а затем аналитически) такую окрестность точки , что .

, , , .

Решение. Удобнее представить функцию в виде

= = = .

График этой функции получается из графика функ­ции растяжением в 3 раза вдоль оси (получим ), сдвигом вправо на 1 единицу (получим ) и, наконец, сдвигом вверх на 1 единицу (получим ) . Через концы интер­вала на оси (центром этого интер­вала является значение функции ), проведём прямые, парал­лельные оси , до пересечения с графи­ком функции. Через точки пересече­ния проведём прямые, парал­лельные оси . На оси получим искомую окрестность точки . Эта окрестность является интервалом . (Концы интервала легко найти, решая уравнения и ). Обратим внимание, что точка не является серединой интер­вала , однако, этот интервал яв­ляется окрестностью точки . Заме­тим также, что в качестве искомой ок­рестности точки можно взять любую окрестность, содержащуюся в интервале , например, сим­метричную окрестность .

7.20 Найти . Пусть . При каком значе­нии функция будет непрерывна в точке ? Верно ли, что при всех дру­гих значениях функция будет иметь устранимый разрыв в точке ?

, .

Решение.

= = =

= = = = = = .

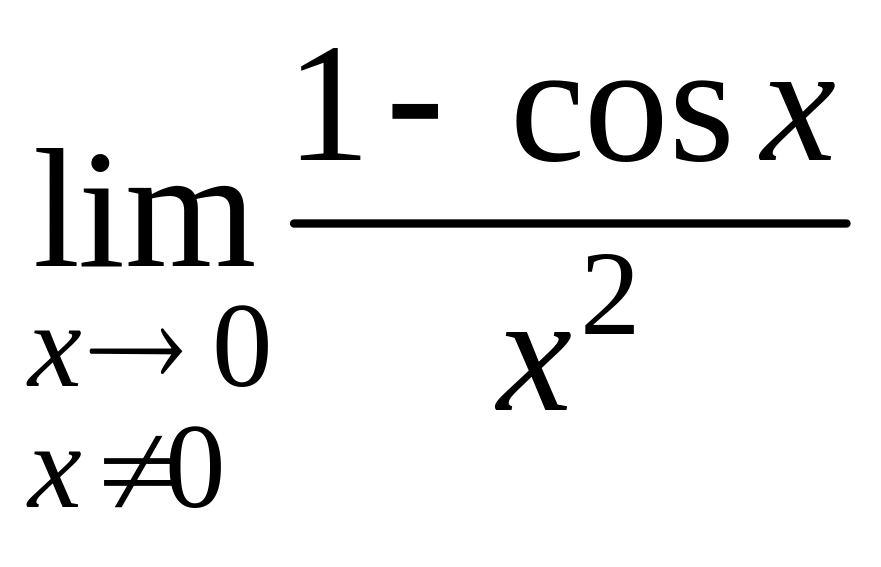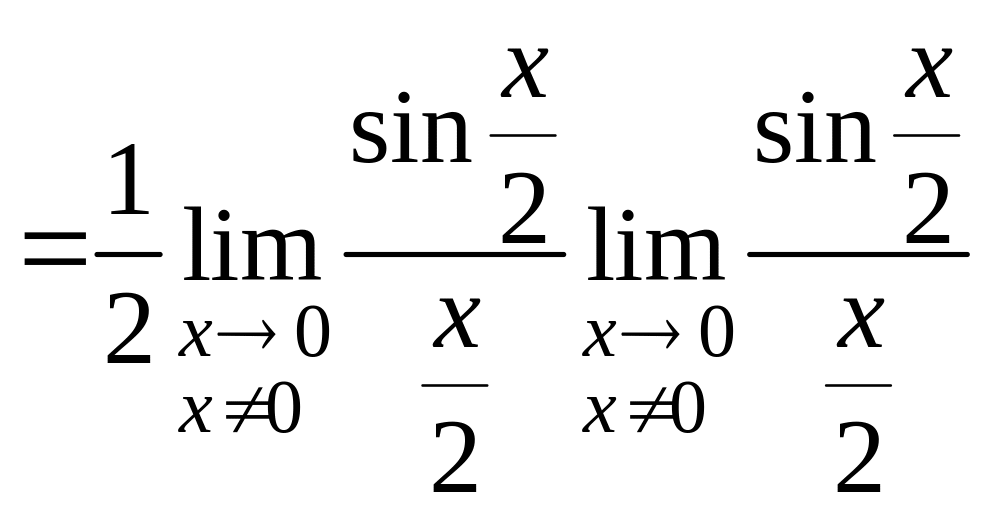Так как при , то = = . Из этого сле­дует, что непрерывна в точке тогда и только тогда, когда , то есть, когда . Так как суще­ствует и конечен, то при функция будет иметь в точке устранимый разрыв.

8.20. Пусть = . (Здесь и далее , , обозна­чают, соответственно, функции «целая часть», «дробная часть» и «функ­ция Дирихле»).

Найти , , , или доказать, что этот пре­дел не существует. Непрерывна ли функция в точке ? Если «нет», то является ли точка точкой устранимого разрыва? Если «нет», то является ли точка точкой разрыва первого рода? Является ли точка точ­кой разрыва второго рода?

, .

Решение. Найдём . Так как = , и =2, то = = = . Отметим, что этот предел не равен значению функции в точке ( ): функция не является непрерывной справа.

Найдём . Так как = , то вопрос о существова­нии и величине предела сводится к вопросу о существовании и величине предела . Так как и = , то и = . Итак, функция в точке имеет разрыв второго рода.

9.20. Пусть . Определить характер точек раз­рыва в точках и (или доказать непрерывность в этих точках) и постро­ить график функции , если , , .

Решение. Найдём односторонние пределы в точке :

= = .

= .

1) обосновывается существованием предела при , стоящего справа от знака равенства;

2) после замены используем тот факт, что ; мы его уже использовали при вычислении пределов в лабораторной работе № 9, то есть мы уже пользовались непрерывностью функции в произ­вольной точке .

Таким образом, точка является точкой разрыва второго рода (один из односторонних пределов бесконечен). При этом точка является точ­кой непрерывности справа.

Найдём односторонние пределы в точке :

= не существует.

Действительно, последовательность стремиться к , а соответ­ствующая последовательность значений функции = стремиться к . Последовательность тоже стремиться к , а соответствующая последовательность значений функции стремиться к . Если бы существо­вал, то пределы этой функции по любым последовательностям, стремя­щимся к , были бы равны.

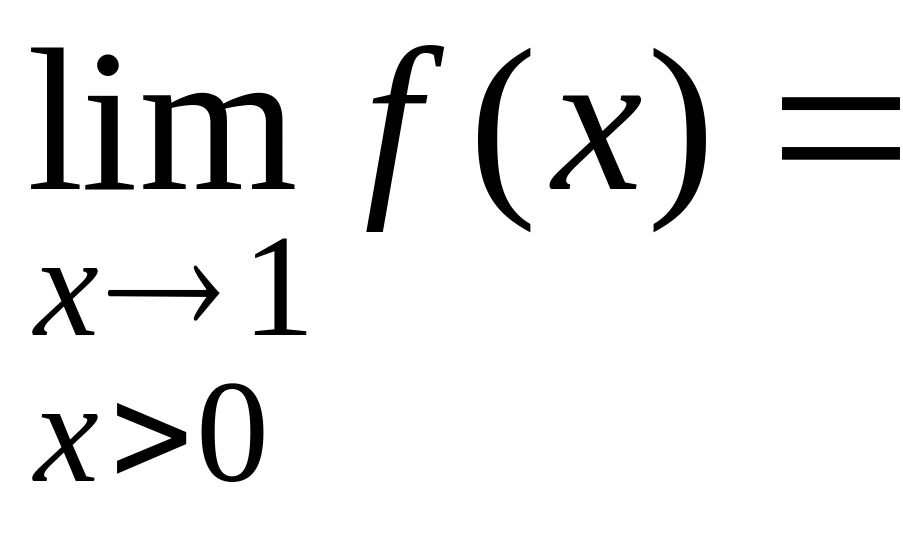
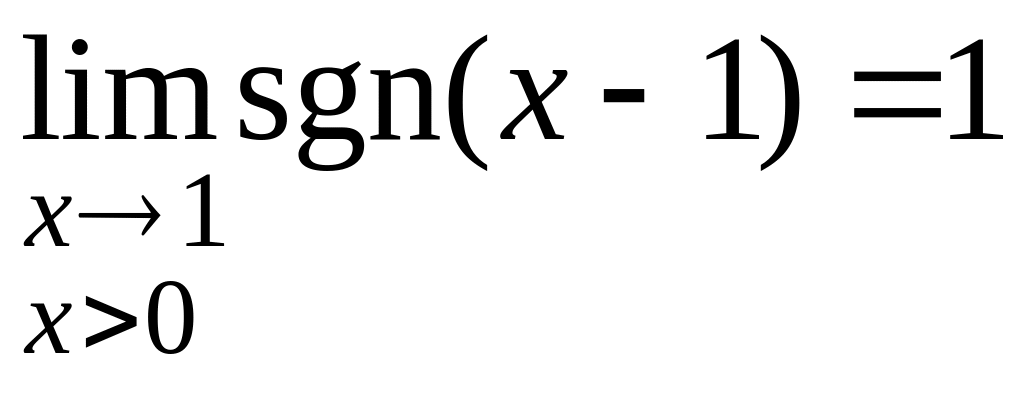
Таким образом, точка также является точкой разрыва второго рода (один из односторонних пределов не существует). При этом точка 1 не яв­ляется точкой непрерывности справа, так как предел справа не равен зна­чению функции в этой точке ( ).

Лабораторная работа № 11

Исследование функций на непрерывность

Необходимые понятия и теоремы: теоремы о непрерывности суммы, произведения, частного и композиции непрерывных функций, теорема о непрерывности обратной функции, понятие элементарной функции, тео­рема о непрерывности элементарных функций,

Литература: [1] с. 169 – 178; 185-195.

1 Используя непрерывность основных элементарных функций и тео­ремы о непрерывности суммы, произведения и частного непрерывных функций, доказать непрерывность функции во всех точках области определения :

№			№
1.1			1.11
1.2			1.12
1.3			1.13
1.4			1.14
1.5			1.15
1.6			1.16
1.7			1.17
1.8			1.18
1.9			1.19
1.10			1.20

2 Функции и являются композициями функций и в разном по­рядке. Найти функцию . Выяснить, в каких точках функция должна быть непрерывной и какому условию должно удовлетворять , чтобы по теореме о непрерывности композиции непрерывных функций можно было сделать заключение о непрерывности в точке функций и :

№			№
2.1			2.11
2.2			2.12
2.3			2.13
2.4			2.14
2.5			2.15
2.6			2.16
2.7			2.17
2.8			2.18
2.9			2.19
2.10			2.20

3 Найти естественную область определения элементарной функции . Используя непрерывность основных элементарных функций и тео­ремы о непрерывности суммы, произведения, частного и композиции не­прерывных функций, доказать непрерывность функции во всех точ­ках своей области определения:

№		№
1	2	3	4
3.1		3.11
3.2		3.12

1	2	3	4
3.3		3.13
3.4		3.14
3.5		3.15
3.6		3.16
3.7		3.17
3.8		3.18
3.9		3.19
3.10		3.20